From 76723ea3ce1735cdc19e3ce4cece494e5af31d0b Mon Sep 17 00:00:00 2001
From: Alessandro Romeo <a.romeo@cineca.it>
Date: Fri, 23 Feb 2024 10:04:22 +0000
Subject: [PATCH] updating files
---
2024_notes/Day 2/01_Benchmark.ipynb | 559 --------
.../Day 2/02_SerialCodeOptimization.ipynb | 1155 -----------------
2 files changed, 1714 deletions(-)
delete mode 100644 2024_notes/Day 2/01_Benchmark.ipynb
delete mode 100644 2024_notes/Day 2/02_SerialCodeOptimization.ipynb
diff --git a/2024_notes/Day 2/01_Benchmark.ipynb b/2024_notes/Day 2/01_Benchmark.ipynb
deleted file mode 100644
index bc5a669..0000000
--- a/2024_notes/Day 2/01_Benchmark.ipynb
+++ /dev/null
@@ -1,559 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "id": "10fb3eb9",
- "metadata": {},
- "source": [
- "# Benchmarking Julia\n",
- "\n",
- "1. Define the sum function\n",
- "2. Implementations & benchmarking of __sum function__ in: \n",
- " * Julia (built-in) \n",
- " * Julia (hand-written) \n",
- " * C (hand-written) \n",
- " * python (built-in) \n",
- " * python (numpy) \n",
- " * python (hand-written) \n",
- " \n",
- "Consider the __sum__ function `sum(a)`, which computes\n",
- "$$\n",
- "\\mathrm{sum}(a) = \\sum_{i=1}^n a_i,\n",
- "$$\n",
- "where $n$ is the length of `a`."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "5812ea46",
- "metadata": {},
- "source": [
- "## 1. Julia built-in `sum` function"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "a17adb59",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "import Pkg; Pkg.instantiate()"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "12536e98",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "a = rand(10^7) # 1D vector of random numbers, uniform on [0,1]"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "1c220406",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "@which sum(a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "8a7ab7a3",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "sum(a)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "4fcbcdbe",
- "metadata": {},
- "source": [
- "The expected result is ~ $ 0.5 * 10^7 $, since the mean of each entry is 0.5. \n",
- "So let's try to time the execution time of this function by using `@time` macro:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "edd112c1",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "?@time"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "320efc31",
- "metadata": {},
- "source": [
- "So what is the performance of Julia's built-in sum? "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "3b17f7df",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "@time sum(a) # try to repeat the execution of this cell!"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "69d7b634",
- "metadata": {},
- "source": [
- "The `@time` macro can yield noisy results, so it's not our best choice for benchmarking!\n",
- "\n",
- "Luckily, Julia has a `BenchmarkTools.jl` package to make benchmarking easy and accurate:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "40217f68",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "import Pkg; Pkg.add(\"BenchmarkTools\")"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "a916508a",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "using BenchmarkTools"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "4efb5fcf",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "@benchmark sum(a)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "3bfc362f",
- "metadata": {},
- "source": [
- "If the expression to benchmark depends on external variables, one should use `$` to \"interpolate\" them into the benchmark expression to avoid the problems of benchmarking with globals. Essentially, any interpolated variable `$x` or expression `$(...)` is \"pre-computed\" before benchmarking begins. So in short with `@btime` `$` is used to \"interpolate\" them into the benchmarked expression in order to get a correct benchmark results."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "bcc80f47",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "@benchmark sum($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "5b8abfde",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "x = 1\n",
- "@btime (y = 0; for _ in 1:10^6 y += x end; y)\n",
- "@btime (y = 0; for _ in 1:10^6 y += $x end; y)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "777708f1",
- "metadata": {},
- "source": [
- "We have seen before the performances of Julia built-in sum function. Let's save them in a dictionary:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "ac55aa78",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "j_bench = @benchmark sum($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "ddf52068",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "d = Dict()\n",
- "d[\"Julia built-in\"] = minimum(j_bench.times) / 1e6\n",
- "d"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "2af9911a",
- "metadata": {},
- "source": [
- "But that could be doing any number of tricks to be fast, including not using Julia at all in the first place! Of course, it is indeed written in Julia, but would it perform if we write a naive implementation ourselves? \n",
- "\n",
- "\n",
- "## 2. DIY Julia `sum` function"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "05bdb0a4",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "FIXME mysum(A)\n",
- " s = 0.0\n",
- " for FIXME\n",
- " s += a\n",
- " \n",
- " return FIXME"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "7ef98bdf",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "TO HIDE\n",
- "\n",
- "function mysum(A)\n",
- " s = 0.0\n",
- " for a in A\n",
- " s += a\n",
- " end\n",
- " return s\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "22454cc3",
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "j_bench_hand = @benchmark mysum($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "d269e7d2",
- "metadata": {},
- "outputs": [],
- "source": [
- "d[\"Julia hand-written\"] = minimum(j_bench_hand.times) / 1e6\n",
- "d"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "545ab9e4",
- "metadata": {},
- "source": [
- "So that's about 2x slower than the builtin definition. We'll see why later on.\n",
- "\n",
- "But first: is this fast? How would we know? Let's compare it to some other languages..."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "7c591bf6",
- "metadata": {},
- "source": [
- "## 3. C `sum` function\n",
- "\n",
- "C is often considered the gold standard: difficult on the human, nice for the machine. Getting within a factor of 2 of C is often satisfying. Nonetheless, even within C, there are many kinds of optimizations possible that a naive C writer may or may not get the advantage of.\n",
- "\n",
- "If you do not speak C, do not read the cell below, but one could be happy to know that it is possible to put C code in a Julia session, compile it, and run it. Note that the `\"\"\"` wrap a multi-line string."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "6c1e8f7d",
- "metadata": {},
- "outputs": [],
- "source": [
- "using Libdl\n",
- "C_code = \"\"\"\n",
- " #include <stddef.h>\n",
- " double c_sum(size_t n, double *X) {\n",
- " double s = 0.0;\n",
- " for (size_t i = 0; i < n; ++i) {\n",
- " s += X[i];\n",
- " }\n",
- " return s;\n",
- " }\n",
- "\"\"\"\n",
- "\n",
- "const Clib = tempname() # make a temporary file\n",
- "\n",
- "\n",
- "# compile to a shared library by piping C_code to gcc\n",
- "# (works only if you have gcc installed):\n",
- "\n",
- "open(`gcc -fPIC -O3 -misel -xc -shared -o $(Clib * \".\" * Libdl.dlext) -`, \"w\") do f\n",
- " print(f, C_code)\n",
- "end\n",
- "\n",
- "# define a Julia function that calls the C function:\n",
- "c_sum(X::Array{Float64}) = ccall((\"c_sum\", Clib), Float64, (Csize_t, Ptr{Float64}), length(X), X)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "d3b912c0",
- "metadata": {},
- "outputs": [],
- "source": [
- "c_sum(a)\n",
- "c_sum(a) ≈ sum(a) # type \\approx and then <TAB> to get the ≈ symbol"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "f2659088",
- "metadata": {},
- "outputs": [],
- "source": [
- "c_bench = @benchmark c_sum($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "b64d7233",
- "metadata": {},
- "outputs": [],
- "source": [
- "d[\"C\"] = minimum(c_bench.times) / 1e6 # in milliseconds\n",
- "d"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "69124ca3",
- "metadata": {},
- "source": [
- "## 4. Python's built in `sum`\n",
- "The `PyCall` package provides a Julia interface to Python:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "34a95ee9",
- "metadata": {},
- "outputs": [],
- "source": [
- "import Pkg; Pkg.add(\"PyCall\")"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "357dd956",
- "metadata": {},
- "outputs": [],
- "source": [
- "using PyCall"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "99f540ab",
- "metadata": {},
- "outputs": [],
- "source": [
- "# get the Python built-in \"sum\" function:\n",
- "pysum = pybuiltin(\"sum\")"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "986968c8",
- "metadata": {},
- "outputs": [],
- "source": [
- "pysum(a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "89ec8102",
- "metadata": {},
- "outputs": [],
- "source": [
- "py_list_bench = @benchmark $pysum($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "35c95364",
- "metadata": {},
- "outputs": [],
- "source": [
- "d[\"Python built-in\"] = minimum(py_list_bench.times) / 1e6\n",
- "d"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "9084038c",
- "metadata": {},
- "source": [
- "## 5. Python's DIY `sum`\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "eb87f43b",
- "metadata": {},
- "outputs": [],
- "source": [
- "py\"\"\"\n",
- "def py_sum(A):\n",
- " s = 0.0\n",
- " for a in A:\n",
- " s += a\n",
- " return s\n",
- "\"\"\"\n",
- "\n",
- "sum_py = py\"py_sum\""
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "d78d2891",
- "metadata": {},
- "outputs": [],
- "source": [
- "py_hand = @benchmark $sum_py($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "38b153bc",
- "metadata": {},
- "outputs": [],
- "source": [
- "sum_py(a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "a55fc8ec",
- "metadata": {},
- "outputs": [],
- "source": [
- "d[\"Python hand-written\"] = minimum(py_hand.times) / 1e6\n",
- "d"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "84e1a285",
- "metadata": {},
- "source": [
- "## 6. Summary"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "7e01b8ed",
- "metadata": {},
- "outputs": [],
- "source": [
- "for (key, value) in sort(collect(d), by=last)\n",
- " println(rpad(key, 25, \".\"), lpad(round(value; digits=1), 6, \".\"))\n",
- "end"
- ]
- }
- ],
- "metadata": {
- "kernelspec": {
- "display_name": "Julia 1.10.0",
- "language": "julia",
- "name": "julia-1.10"
- },
- "language_info": {
- "file_extension": ".jl",
- "mimetype": "application/julia",
- "name": "julia",
- "version": "1.10.0"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 5
-}
diff --git a/2024_notes/Day 2/02_SerialCodeOptimization.ipynb b/2024_notes/Day 2/02_SerialCodeOptimization.ipynb
deleted file mode 100644
index 7466c51..0000000
--- a/2024_notes/Day 2/02_SerialCodeOptimization.ipynb
+++ /dev/null
@@ -1,1155 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "id": "37a71ff3",
- "metadata": {},
- "source": [
- "# Serial code optimization\n",
- "\n",
- "Several decisions can be considered while designing the code (e.g. Types, Type Inference, and Stability, multiple dispatch, meta-programming, vectorization, ...). Such methodologies allow to write an efficient computer program for high performance computing.\n",
- "\n",
- "Before writing any fast parallel code, one should consider write a fast serial code. Here are some tips that could make your serial code run faster: \n",
- "1. __Write your performance critical code inside a function__ \n",
- " Code inside functions tends to run much faster than top level code, due to how Julia's compiler works. Functions not only enhances the performance but it is more reusable and testable. \n",
- "2. __Make variables local__\n",
- " A global variable could change its type during execution, so it could be difficult for the julia compiler optimize it. Using local variable instead or declaring the global variable as constant (`const:`) will greatly improve performances.\n",
- "3. __Use `@time` or `@btime`__ \n",
- " Use `@time` or `@btime` macro to measure the execution time of a function. They can also indicate the amount of allocated which could be sometimes significant. \n",
- "4. __Declare types when possible__ \n",
- " Type stability makes for loops faster. Declaring types help compilers to convert into machine code."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "983794bc",
- "metadata": {},
- "outputs": [],
- "source": [
- "function xpow(x)\n",
- " return [x x^2 x^3 x^4]\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "86c8219c",
- "metadata": {},
- "outputs": [],
- "source": [
- "function xpow_loop(n)\n",
- " s= 0\n",
- " for i = 1:n\n",
- " s = s + xpow(i)[2]\n",
- " end\n",
- " return s \n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "db90c677",
- "metadata": {},
- "outputs": [],
- "source": [
- "using BenchmarkTools; @btime xpow_loop(1000000)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "a9fafbc8",
- "metadata": {},
- "outputs": [],
- "source": [
- "x = 0.0\n",
- "@time for i = 1:10e4\n",
- " global x\n",
- " x += i\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "cb482534",
- "metadata": {},
- "outputs": [],
- "source": [
- "function sum!(x)\n",
- " x = 0.0\n",
- " @time for i = 1:10e4\n",
- " global x\n",
- " x += i\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "a05f1ff7",
- "metadata": {},
- "outputs": [],
- "source": [
- "sum!(10)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "1ebd5490",
- "metadata": {},
- "outputs": [],
- "source": [
- "function sum!(x)\n",
- " x = 0.0\n",
- " @time for i = 1:10e4\n",
- " x += i\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "d35bc8fb",
- "metadata": {},
- "outputs": [],
- "source": [
- "sum!(10)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "35df028c",
- "metadata": {},
- "outputs": [],
- "source": [
- "function sum!(x::Int64)\n",
- " x = 0.0\n",
- " @time for i = 1:10e4\n",
- " #global x\n",
- " x += i\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "cf5dece6",
- "metadata": {},
- "source": [
- "sum!(10); x"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "1f9ff500",
- "metadata": {},
- "source": [
- "# Julia Array-type optimization \n",
- "Arrays are a fundamental data structure in all programming languages. Moreover, they can improve performance. Thus, a special attention is given to the usage of array in numerical programming.\n",
- "\n",
- "We will discuss how to use arrays in Julia in the most efficient way:\n",
- "- Computer memory model and array representation and storage in Julia\n",
- "- Bounds checks and **@inbounds**\n",
- "- Specialized array types\n",
- "- __Broadcasting__\n",
- "- __SIMD__ parallelization"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "35080185",
- "metadata": {},
- "source": [
- "## Computer memory model\n",
- "\n",
- "### Key elements of a CPU \n",
- "- The control unit (CU), which turns binary into timing and control signals.\n",
- "- The arithmetic logic unit (ALU), which does \"the math\".\n",
- "- The cache, which is a place to store data and instructions for quick access. The cache stores quick-to-access versions of what is in main memory (RAM).\n",
- "- The registers, tiny little caches that the ALU can get to directly.\n",
- "\n",
- "**Core** \n",
- "CPUs are composed of one or more smaller cores. For example, a dual-core processor has two ALUs, one or more CUs, and may have caches unique to them (though commonly L2 or L3 are shared).\n",
- "\n",
- "**Memory model: High Level View**\n",
- "\n",
- "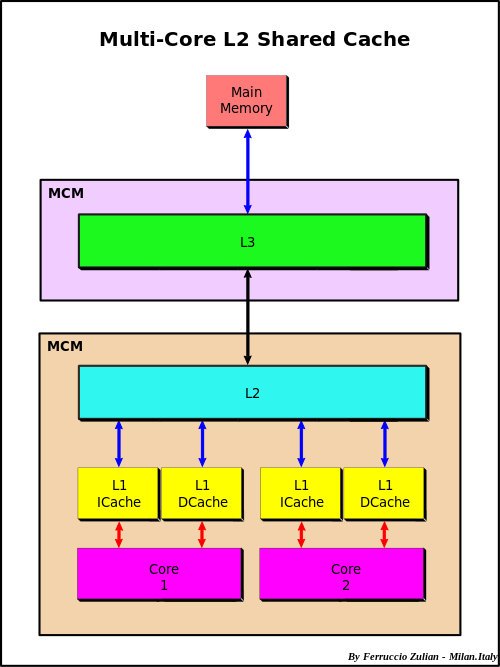\n",
- "\n",
- "1. **L1-cache**\\\n",
- " A CPU's core memory accesses directly L1 cache which is very close to the processor. It is really fast (a typical latency ~ 0.8 ns). As thumb rule, the things we need to use soon, are kept there. There can be two L1 caches: Icaches (Instruction) and Dcaches (Data). \n",
- "2. **L2-cache**\\\n",
- " L2 is a larger cache that's a bit slower (a typical latency ~ 2.4 ns). \n",
- "3. **L3-cache**\\\n",
- " L3 is a specialized cache designed to make L1 and L2 work better. It is slower than L2 and L3 (a typical latency ~ 11.1 ns). \n",
- " \n",
- "\n",
- "**Why worry about this?**\n",
- "- For optimizing purposes, the important parts are the three cache levels (L1, L2, L3).\n",
- "- We should use the things that are already in a closer cache. The code will run faster since data doesn't have to be queried for and move up this chain.\n",
- "\n",
- "**Cache miss** \n",
- "A *cache miss* happens when something needs to be pulled directly from main memory. Caches store instructions and data. When the ALU needs data to do some math (x + y), it has to ask the cache in order if they are available. If not, you may need to go and retrieve it from RAM, but this operation can have a very important computational cost. \n",
- "Cache-aware and cache-oblivious algorithms are methods which change their indexing structure to optimize their use of the cache lines. "
- ]
- },
- {
- "attachments": {},
- "cell_type": "markdown",
- "id": "b281adc6",
- "metadata": {},
- "source": [
- "### How are arrays stored?\n",
- "\n",
- "When an array is allocated, the contiguous storage simply consists of pointers to the actual elements."
- ]
- },
- {
- "attachments": {
- "pointers.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAADrCAYAAAB6v6EcAAABPmlDQ1BJQ0MgUHJvZmlsZQAAKJFjYGDiSSwoyGFhYGDIzSspCnJ3UoiIjFJgf8bAxMDPwAnEMonJxQWOAQE+QCUMMBoVfLvGwAiiL+uCzLp9qneX98mX6xNmXItjMGSOxVSPArhSUouTgfQfII5PLigqYWBgjAGylctLCkDsBiBbpAjoKCB7CoidDmGvALGTIOw9YDUhQc5A9gUgWyA5IzEFyH4AZOskIYmnI7Gh9oIAq5G5kyEBd5IMSlIrSkC0c35BZVFmekaJgiMwdFIVPPOS9XQUjAyMjBgYQGENUf1ZDByGjGKnEGJFqxgYrOsZGJi+IcSinzEwrLnBwCC4HyGm4cbAIA4Mj33lBYlFiXAHMH5jKU4zNoKweYqA3vzx//9nWQYG9l0MDH+L/v//Pff//79LGBiYbzIwHCgEAGmsXtKRMhyuAAAAYmVYSWZNTQAqAAAACAACARIAAwAAAAEAAQAAh2kABAAAAAEAAAAmAAAAAAADkoYABwAAABIAAABQoAIABAAAAAEAAAGMoAMABAAAAAEAAADrAAAAAEFTQ0lJAAAAU2NyZWVuc2hvdLA7jrYAAAI9aVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA2LjAuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIgogICAgICAgICAgICB4bWxuczp0aWZmPSJodHRwOi8vbnMuYWRvYmUuY29tL3RpZmYvMS4wLyI+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj4yMzU8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICAgICA8ZXhpZjpVc2VyQ29tbWVudD5TY3JlZW5zaG90PC9leGlmOlVzZXJDb21tZW50PgogICAgICAgICA8ZXhpZjpQaXhlbFhEaW1lbnNpb24+Mzk2PC9leGlmOlBpeGVsWERpbWVuc2lvbj4KICAgICAgICAgPHRpZmY6T3JpZW50YXRpb24+MTwvdGlmZjpPcmllbnRhdGlvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+CpQnZWYAAEAASURBVHgB7Z0HYBTV1sf/20t67wkJJSH03rsUEVEUxIZdn2JFUdHn53uWZ++8Z+8VOyiC9C5SpQihEwhJICG9Z9t3zyQTNkvKJtksKefqktmZO3fu/c3O/c+55xaFTQRwYAJMgAkwASZQDwFlPcf5MBNgAkyACTABiQALBv8QmAATYAJMwCkCLBhOYeJITIAJMAEmoLZHMH36dKxatQrR0dGYOnWq/SHeZgJMgAkwgVZC4JdffsHJkycxbtw4/PDDDy7LtcLe6a1QKFyWMCfEBJgAE2ACF56AK/s1VbMw7IsWHh5u/5W3mQATYAJMoJUQSEtLa5acVhOMiy++GEuXLsWECROwbNmyZrkgJ8oEmAATYALNS2DixIlYvnw5qE53ZWCntytpclpMgAkwgTZMgAWjDd9cLhoTYAJMwJUEWDBcSZPTYgJMgAm0YQIsGG345nLRmAATYAKuJMCC4UqanBYTYAJMoA0TYMFowzeXi8YEmAATcCUBFgxX0uS0mAATYAJtmAALRhu+uVw0JsAEmIArCbBguJImp8UEmAATaMMEWDDa8M3lojEBJsAEXEmABcOVNDktJsAEmEAbJsCC0YZvLheNCTABJuBKAiwYrqTJaTEBJsAE2jABFoyWfnNtNoj/OTABJsAELjgBFwqGFQVn9uOH1+7HTfd9hKQ8i3sLZ8nC76/chGm3vYd9uSZcuDrWhpyj6/DB8w/jtlkzcPHIQZh0w3+wZFcaSkWmrOXpWPHuo7hyTH90S+iCjnFxiImJQmRkGEJDo9B77J344Pd9yDXZYCk4hO9fvBPDEjqhU7dhuHbOfKzYU5GOe+Hy1ZgAE2ACQLX1MJoGxAaruQi5Z88gq6AQZWarSE7VoCStpmKk716E1z/eg8G3PYwr+/rD6TUAbafw5y8bsOJ4Ea5/+Dp08VRDo3b6bId8WpG+7Qu8seAEBs+8GeN7R8BT65y2WksP4vtXnsXLP29DSk4JfIJj0DVCIcpRIWGm9N34bfEqbNq+B5nFQlTJgqi6uh7asFwUFpfDQjttFpSXFaO0JA8paSeQllEMY0AkOkRPRWffhrGtugRvMAEmwAQaScCFgqGCd1hf3PB/H2KmRQOjh6bBWbKai3F0629Y8P1GpHWfjmlCMOqqFm22Uuxe8Ajunn8c/cd3xtG0XJQVJuHDx6bj6WNemPvhu7i6bwA0ztX1dvm14OiWH/Hdgt3Iih6JgQmhTgtGeepB/Pm3WO0qbjrefOJOTB4YBx+9EUaDDiqhX2WmUuSXlsOzx9V4dO6duHRANPQKJZRSHhXQaD3g6e0BvVaIjCYeMx55G5PuTMGqD5/Dy5//hcKCApSV22WVN5kAE2ACbiLgQsEAFEoVtAZPaBuZeavNipJisk5sUCmdyZp4bzcV4czBNfhw7xpYSopgthZg9ZLDCOgyVWSokRmxmUQ+ylBusoDWOXc+GRtMRbnILCyDKiQAYWKZ25AAf4i6vypYTGUoKjFD7SmOR0QiKjKiGq9q66oLIdEavBCgDUGgnxFatQVWq4V9GlU0eYMJMAF3EnCmVnYyP1YUZR7Gqu/ex69HOmL2Y7dCvPPj98/fxm+pvTD7riE4u+ln/PDrWuw5YUP3sZfg8quuweT+4dAorCgrOIXf334M/3x9NXIKyrD8+asxbu0NePmtuRgQXLO1olBo0eOql7Gs+yWY/8hDmL+6SDTjmBDU7168885jGNfVT7IuzDk78L8n30Px8GsxzHgEK39fhQ1bj0DdYTAuvWoWZl7cG0GeWkgv+eZU/PrKE/jX/3bgbHYufnn5FhzcfAeefvpWDInT4++fXsY7y0rQrV80ipJ3488/dyJD2w03PfgoZo7qCoNaA6UQGWu5RYiXfXMTYbShuCAPpeUmqAK10GnVUFnMsCpUwsJQCnGqBTXtl5qoRBz6r7Z4tZzOu5kAE2ACriDgQsGwoCgnGdtXLsOqQ3G46ObrEa47jq3LfsfPOxZh0xItsjKzUFZagnKzAklH92H9mv2wfvEmLu/qISpEKyxlJSgT1bbFUo6czDRk5ojK1VRXMRVQa3XI378ay/ecgSY4HnFeGTiy6zvMf7834p66Dl39dShL3Y2Fi3/Bnq9/wquwwlRehrIykfD+A9i2eik23vUynn/oYsT66SXRMJUUwyJETLidkZmeicCzuSgxie/WHBzYtAGrftuFH34UNbjVJMpTBkOoBzJziyEMIyi0evga1LCVl4vrCIuAKvqqCt6GgpwMFIvr55/cgk+fvh1vnjiCM+ZA9Bo5FddefyVG9o6Fr96hIU74MizCJ2QVDXRKtUpYcnUx4WNMgAkwgeYh4MKqR7xNi+aSclERm6hyo76goqIziYozPzdTVP4aDL/2X/jqtw34c8MveO7G3ihOXoHPftiCQuEf13pFYdztz+Kxa+Lh5xuD6//zI377fB4GhdVsXVTgENe0JGP5F8uQrOiBOa98gR8/fRlX99Ji85dP4MmPt6JINCuJ2la0+1M+yhA54Go89c4P2LhjB9Z8+ywmdbZgzScv4NPlh4RvQcRVh+LiOc/igSsS4O8djpue/hxfvfcwxnQOgE6IiNksyldehBJDZ1wx5y0sWrcNm9cuwP1TeyHIKHwRGh2MGpXQEiEYgke1YM3FkX37kZlXiPT9W7By+Rrh7ziKw0nbsfiLF3D3Px7EG99tRmqBudppZF5YrQKSjayLOiwRh7P4KxNgAkzAlQRcaGFI1Zp4C7ZBqRNvwtRuIj4KlRoB0b1x42Mv4r4Z/RHipYda+Bk8C8Zj0c+7sXftX0iZOxqJBhX0nj7w1ANmhQYBkXGICvGt0+lNr+4KdUfMfPpVJBR3wohBXeCj6Ybn3wlCt++2IGRQDHSiqYc62dKLfnDfG/H0S/MwunMwPHTCCoiPxT+LT+Lvez/Hwu9X4fKRsegV5gWDl8iHlpqWdAgMj0aEyIeePOcWck6LsumicMXtD2PObROREOoJtarmSlzSTPu7pTAgqmt/9O6RifD+HTFiwgSMHNAZPraz2L7kC7zzxUp8/dGXiIoKxTWjOkHoj12gMlApRKj8U/GF/2UCTIAJuIeASwWDmpXE/yKoK3r9SL1/1NB5RKL/kP6I8veoaJ2x6eATLhy+ounlQPYZZJOJIQSDvLkWYQ3YRCyVEJqqlpy6WCj0iOo7EWHimlrxZi8aqRDWfSJmdxgFpd5T6lort2p5hMQiJtwfHgZthRBpPRE/djLGRP+Ib3b9hSOni5AY7CVSEM1jol+rcL2LfAiRqMqIorJcnojuEIMgX0q/Wq1eV06FvunReczteKXvtUJ7tKInmQcMesqLBbHRATBlZ+KNRVvw5+a/MVo0TXX0s2uaYsdF3Wz5KBNgAs1OoAG1XX15oSYTajohw0I4c0UfUmo+ES/kUNjMou3dXgDIMhDjJEQcm7VMNGFVpi0qRRIKqqqtVnlnfdcVoz1EM5BOEouKuEqVDl4+PsKKIAGhUPluLqyNc5V/RVyNdyBCfY2wleWjoFg4oMkskARL5BHiu3BCSH4IKToJBpXLKj70tyIN5/8VJ9hKkJOVL1IWFpXoaqum9ESPMI+AePQb2An+xnyknkpBVn6ZyLUc6FpkxQheUv7k/fyXCTABJuA+Ai4UDOEDJsGgZnvR66eiMiUBoOpaOG2lkWhywcQe4fgtEb4OhUovKvuKmlfEhlbvAZ04o4x8D64KIl9U+ZblZUt+inN1rui1lHII+9MLoAuMQmigaC6jwRLi7V8nrB+FUvhgzCQickaEYNBxUd1bxM5z6cjH6/trRfLGj/Ho7Jsw56UfsPtEvrBlKoO1EFkZOWKQHkTvKQM0ogmsgoo4XikWUkbouvI5/JcJMAEm4EYCrhMMqj1FexSJhlKoBNWrCnp7FoWxltGb+rlS2SzCeVxcjEIx/YVS6y2aiCqqRrJC/PxDobGWIvnQMWSXuEo0KirZjF2f4NkXvsHO5GwUFZzF0R2L8erTr2F1qg2DpkxAd9EcJY2ZEL4GvyAf4f+wICX5BHKKSipFQ1TigphNiJlVlKHGUFXL13RUgeCYLghVF2PLLwuwYPFGHEwTHQLSDmDV1//FO1/9gdNisF7PfomI8Ks+moWuS5YNWRgVzX41pc/7mAATYALNR8B1PgwyKcRHHngmpECIBTmJxX7RJFXttVjUeCYxyK5A1Lkeft4wVI5sU2qMiBs4Av2DV2Pd23dg9OrBuPqOeXjgmt7wpHQaGaiStYiPqSAdG796EtMXvwitqsLKKRSZ6DLxPtx3/WCEeWsr3+q16DJ4PHoE78CGDx7AjDXf4Ip/PIQ7p0QJwRDlohr7nNlRPVfiuEpMSVKzEivg2WEEZl49Bn+/uhBfPHuHmHtLjAAXFli54GHx6oTJN9yEK8f2QIDePgWy1IilsNREU11tl66eEf7GBJgAE3AtAdcJhnAVG70jkNi/L5IzeiPSTzi7bSGI79cXfTw6IybQzoEr2uyNATHo2acXogYnIlBq5hEtQWoDQntciadfV+Cbn5dhnXD+7kxKF5P2CcFoQrltwrwxi+k0Qvpehqn9lNi5ZhOOFPmgW58RGDluCi67dDS6dwgQIiKLkhJBPa7Cv17WYeEvS7Fs/REcOpqGgvJOiErsid6i91XXOH/Rc6qmTAmxoGTER9JQhyhKbQAGXnkv/u0RhZ8XLcGaLcdg8YlG34uGY/ykizFmSC/EhHhKFlrVqaKJT0XjL8S4D7PoHix1sRUyw4EJMAEm4E4CLhQMFbxCe2D6nJcwweSBUDFgTqvogql3v4jhpTqEhJ67FPktAjuPwyNv9oLZIwQ+VdaDmEvJEISe464TPZ8m4/bsPCh9o+FbVZE3Eo2wCMjC8I4ehhsfvAwP3FcgmsO08PH1ha+fH3y9DJLz2T51pT4APUfPRHTvCbhOOKk1fuGI8PdC5KUP480RFvgEBsOrxgkJhR+HDKpaHQ1KGPw6YNjUW9Bt+OWYnVcMm1oPTx9fMf7EG0bqNSXrVlWGRA8wPXUkEJaZmFqkvJo/qCoSbzABJsAEmpXAuVq8yZcRzSYaA/xDo+FflZZezNYaDZ+q7/KG6Pyq80ZYB295x7m/4rVcrfdCkBgPERR2bneTtsjCEBU4pesfEolOvjphAFT4V2pPl/LhiUAxziIw1C6Wbxg6+Np9d9i0ilHi+WLqD3NZHs6kpiL9rB/C/byq9eIStpToauyLEPpEOSTg+FUMfiwpKkRhUSnMLBSOdPg7E2ACbiTgQsFwY64beKmKsR0VzviKl/f6xKKBF6iKbkN5qZiO3GJB/okVeP2RbfhATB4Y138a7r7/ZozpFQmj01Ou21CUth3ffvQ+vl66FcmnTiPbHIUrozsg0Jubo6qQ8wYTYAJuI9AuBEMXEo8R/fvA1q8jfMWEf+e1+LgMtwIesSNx6913InLdVuw7eAQnRC+o5ORTOCOansjKaUgwF59F8pFjOJmSiVIxZcng8Vdi6vh+CPdgwWgIR47LBJiAawi0C8HQR47CE292gi0gCn40vsI17GpMRe0ZiZGX3YSeo6Yhv7AQRcWlsGr8EdUhAh5OWxeUtOhRFTkEtzz+OqbcWQSb6EHmFxSKsFAxpxXrRY3seScTYALNS6BdCIZC64MOXc/3pDQPWhUM3gHSp6kuGJXeFx3ixad5MsqpMgEmwAQaRMC+s3+DTuTITIAJMAEm0L4IsGC0r/vNpWUCTIAJNJoAC0aj0fGJTIAJMIH2RYAFo33dby4tE2ACTKDRBFgwGo2OT2QCTIAJtC8CLBjt635zaZkAE2ACjSbAgtFodHwiE2ACTKB9EWDBaF/3m0vLBJgAE2g0ARaMRqPjE5kAE2AC7YsAC0b7ut9cWibABJhAowmwYDQaHZ/IBJgAE2hfBFw2l1RGRga+/PJLrFu3zimCGo0GUVG1LwYhrV1d+ypEtV4jISEBarE2OAWlWC5VpxNrX4g1NkpKSqT1sGs9URzQasUSrSJubGwsjEajtE1p+fj4SGl5eHjAy8sLlHcOLZdAuViV8PPPP8evv/56QTMZGRkp/aZcnQl6NhxDTfsc41yo797e3oiIiDjv8vSs0TNKeS8tFeu9mM2guLTfPlAcejbtA606See4O5hMJqkuCQwMrJbPTp06SWVxzA/VFY7loTqFymQfqF5x3Ef1jaen53lltz/P3dsuE4zTp09jwYIF2LZtm1NlIGi+YsW7ukJjHgJK0x68LB70Y6wvqFQV08DKokA3mj6y6FBa9MPt0KEDLr30UgwdOlQSlvrS5ePuJUCC8dVXX2Ht2rXuvbDD1fzEao7yb8rhkEu/NuY5cWkG6kmMnhmq/GoKcmVKzyeVo6aXMYpTE0dnnumartmUfRax1g2JlV6vr5YMvVTKZbE/UFO+a4on1zH258r1TUxMDKZMmSLVNyQgFzK4TDBIeXNycmotiywQtf1w6ESK06VLFwk8VfqFYnpwgkvn0LZ9oB8XWTXyW8bx48elw1lZWfbRqrbDw8NBFQmF7OxsGAwGKe3OnTtLP9KysjIcOnRIenuoOqmWDX9/f+mNqW/fviwYtTC6kLvpgabfhisCVfqODzg9tI77XHEtxzTIAqeXF/tAFZDjtekZoOfPPlAFRM8CPZOhoaGg3yz9xuVnwD6uM9tFRUXnPYNUYTtW2sXFxThz5owzSTYpDpWP3vLtA9UJjuWj3wI97/ZBrlPs9xHX+Ph4+13Stly/yAfS0tJw9uxZ+atb/tK9CwsLA9U3bUYwqIKX3w7ohz5v3rxqMOk4NfPQp7ZAN43MeLqh9KFmJPpLak7bjoF+CPKDQhVEXW9a9ODLcenHT+JEaUdHR0tvL/RDS0lJOe8BsL/m0qVLsWHDBukHSAJGbxscWh4Buq9UoVCgv6+99lqjM1nT75VeYOgazR2Cg4OlFxv769Bz5HhtEgLH3yI9i2+++SZWr16NESNGYMaMGVJl6ljB26dd1zZVnCQG9oEqY8fr0nOan59vH63e7d27d+P999+XKuz77ruv3vgUgZ5far6yD/T8y8+4vJ/y6Jhv4ifXVXI84kpv8o7BUYCuvfZaKcobb7xxXhqO5zb1+/Lly7F+/foWVd+4zMKgSp1+4ElJSVJT0+zZs5vKq8WdT+2Ue/fuRV5envQGSw8qh5ZHgCoEevH466+/pIe6Lf4WnaFOlSK97VMzLb2dttTwww8/SIIREhKCln6v6GWTwj/+8Y/zmqVczZdaW/7++2/JSszMzJQsRFdfo6HpVfe8NPRsu/g1Kb7d4TaxSTdQdr6xhdFybylZqvX5x1pu7jlnTKCCADWX29c3jbUOXcnTZYJBmXI0lV2ZUU6LCThLgH6H1ATJgQm0FQLU1OfY/HchyuayJqkLkfnWfk3yu1DvstTUVKmdVfbBUFMXHZPNXyonbZPPprmbwejtnCpbxwpXdjJSswE5UWUfATll6+oefaHuUU2+hwuVF74uE2gqAfKlkD/mQgcWjGa4AyQC1HZ86tQpqeKnXhXkjKObTkIg97wg52BBQYHURmnvXCPTk5q87B14dJzi28drhqxLzkQSAepFZh9ISMjZS8eoCyF9p0DxSFzoGPVEo0Bt5wEBAQgKCpL+ksDQMVlkpEgu+IcElth+8803iIuLw7hx46p6vzkKngsux0kwgQtGgBz3LaFJigWjkT8BckKtWLFCuom0TSIhV+a5ublS5U5dGkkQyDogc5I+dKy5rYRGFkk6jX6UlO+6ukjXlD4JBgkJBRIT6v5H++gvCQd1WaReLVSRU+cBGshF+5viayDh/fnnn0E9VqiLJfUqueWWW5CYmCh1I60pn7yPCbRGAu5oXXCGCwuGM5Qq45DFIKs89V4gkSDlr8lKaECybSIqiaJ9E5p9ociyIGEgy4MsEmrWor7lZK2QiFDvOhpdTwJC3Zyph5MzQkJWGI3opjE4ycnJ0jiao0ePgro+0j3hwATaCgFqsahpaIG7y9fGBUNMOZB1FNs3b8bWfbkIio0QFVUY4nv0QGyQB1TKhvWlp6lPyEKgQAN46NOUQM029FZOf+WRo9TMQj0jqEK1bxait3V6O3d1s45j/kkAacCXfXMYxaHKmX60VBHL/ewpDu2nbsZ1BbKo6Fw5HD58WN6UmsBIHEgsSEDIUqBtasaiZiayRGgfCQkNXpIDtedS8x4JBQXiRvkgK4N8QnLzmHSQ/2ECrZwAvYw5PpMXokgtWDCsKC86je0r1iE7dCguGhQDfYPqdxuK07bi8/lv4/s123HoZBG8g/zh6eWHmD6X4q67Z2FYF39onRQNsiZoEI0sGHXdLBIBaoqhio4qQ3qDlit6qghlhyzFI2GwP07p1iQYdI47BUO2pORyklBQpU9iIQsE/YCJB5nL5EuQm+ToTYh4kZiQ+NC58jlyevJfug6dSx85UC8nsjxIOKjMxEm2PkgIqHtzx44dpSYvGpRGU9LIgdLbs2cPTp48Ke/iv0yg1RKgF0UaskDPVptyelOh5IrQJXfHZkHx6Z34+s3XcThegT79oxGhdl4xrCUnseSDVzH/s3UwxwzAyPFB0GnEW2jybmz47l2U60MQPu9ydPI3QOVEsjQSlAY/paenS5UkVWhUaVFFRqJAzSwkEhSPbrIsFGQ9kCDIFoS9YLiEk4sToXvY0PtIvgTy48hvQGSlkPVFQkFv+ydOnJC+01sS8ZPNa3uRsC+GbC3YiwyJCFkgJCBkaVCzFTVjkRBTfumacqDzZR8MPWR//vknBg8eLB/mv0yg1RCgF0r6jdOz06YEgxydDa1o6rprNqsF5TmncODQMRxTCV+BqATESI+6TrE7ZsXpXT/h3S/XIst/KB6e+xgu6x8Og9qG7CMr8cqjT2PpT19g1eShiBoeBaOm/uEoVOnfdNNN2LRpkyQY1Fxyzz33SA5WqsRICKhCI8Fob4HE0LFrbffu3SUMJCJUeVPlTwJCQkK+ILI+SGTIOiFrhLbJWiExqcmKIxEg64Y+JEAkICTMJNx0rLZAb2YvvPCC1JPKvomvtvi8nwm0JAJUp9LLeEsJbsqJDWXFmTi4dROOmDuidwcLjgmn8aHkdJRoI9Czb3/0690Z/vqKytZmLUfW0U34+qvfcLSoRDQtrcJ7r3pg6vSZGNHRE/kn/sSiZYcQ1rsn9NlHceDwMaTme2DAJTMwsXcI1MjDziW/4a9UJYY/9A9cM6kvwjzENMOCenjINFx72SKsfGkLVmw6iMv7h8GgEdOaO3FHqHePPAcNveFScwiNxuRQOwHiRWJLHwr2U1RQrzGyMsgKIdGgbRIDEg2yREhYSCCoWYsExT6QSJDo0KeuQE1UNGvtokWLcPXVV9cVlY8xASZQDwE3CYYZRZkHsOT9V/Fdij+6hFtx6shRnDotBqJpAtG5Wx+Mm3477rhqhKjYxfz4FvFWemIblvy+DWl5YoRj2Xp88WEJAvtMxLAOWpza/j1eeWkJvEQFrs8/heSUdGSbQnBN2DCM7REEpTkFf/1xHEUeXTFhYh8EGirEglgo1L7oNXwIIv63EQd37sfZkmEI8dKiYlRBPbT4sEsJkFVKTXn0kQMJAVkiJBbJwqFNYkHiQR/yS9AEkSQwDelwQOm9+uqrUhPigAED5EvxXybQaghQM2xLsJDdIxg2M0wlZ3Hy4HHs3rsDKRHx6NOrDy4aKNauKD6D/X9txKfzi+AVEoG7J3eCVqWBf4cBuHh8P+w7tRrWDsMwbdoUDOwgFleBFfkZKUg5flj4I86i27CRGHnJcNE0EYKh3YOhVilhyTuDE6nF0PgmIj7Wy8FHoYBvZCfEeOmw/lgaskrNsIoWDWf8GK3m19WKMyo7vGksBX3kQE1LR44ckT7UdZa2abGuffv2yVFq/Uttvzt37pSapqinW0t48GrNLB9gAnYE5OZWEgxXNvnbXaJBm+4RjKosKeEd2BmTb34Yd145AvExgVAWHMPqr1/DU68uwdcf/4oJQ+9Dd1/RrbTDEEy/dIjwQ/wBY5+ZePyfsxCpU8JqLoZC9GxSKg2I7jcVc/5vLi4dFAcfYUVoNGLKcnGtspJCFJktUOlFbyWDaOZyaG9SGYXzVKtCWX4RSsotqL0FvCrjvHGBCVDPMVlEyGL44IMPsHHjRqdzRaKxcuVK6Zzx48c7fR5HZAIXkgD5/uhliV5y5ObwC5kfN3toRU+qgJ64bOYVGNItGv6eRviGxmP0tJm4qKsRydt/x7ZjFdMHExTJ8S3WhVFpddBW9ZAisVCJjw4JF8/CzLGJCPI2QFspFnSeSu8BD40K5tI8FBaL+VccFMFqLkOpxQqNQQeNsEg4tC4C5BT/73//K3WfdTbn1BmhV69e7bJTgrOMOF7LI0AdRmgcEwlGS+hQ4zILgzz51GulrkD1tlLlAaPezmOgUMPg3xk9e/jDuicFyakFsPU9tzBKhXFQvcaXwAkrQ+/tBX0NbUlKrwh0jPGAZfteHDiej5HhYpBelZUhetucEj2v8srh212sRGZU2x2rK/fVj1FX0pbQza16rtrHN3Jkk2PcmUBvZdQ5gayTyy+/XJpvypnzOA4TaAkE5PEX5O9rc4JB3UprCzbxmk/tcTZLiZh8z36lOhuspkLRG8YEpVrMPySaliqCsCTUYioJ8dVSbob9GWRhkNVgNtc8e6NSG4X+o7rAc/12rFi+E9P6TEC4Z4Xj22bOxR7RlHFcdK7p3jseweICjbExWsp0w7Xxbqv76TdEYm0/7sK+rPRQURdnuj9kztMI8WeeeUZaD9k+Hm8zgdZEgF7Iyb93oUNj6spG55mamEpykrB8yVocySwUbXMlyEk/jC0rf8bSrWfh22kw+nfxrXA5CAtC7emNANHVtjgrA1mF5VUtSwoa6yAc6RaRXo1B4YXeE6aif5QCWxd+iO9X7EZ6XinKS7JwcPMifP7jdpR6JWLciET46c/1oKoxLd7ZogjQuA7qKWUf6GGicTGjR4+Wxsrcdddd0ih7Eg8a3Dd06FD76LzNBFodgZYgFgTNZU1S9d4ByboQs7VmJOHnd59HUfIGxPmrUJB5Evt3bsE+cydcecN16BdRYWEolMLfEdIJvTr44Nv9v+G/L6kwesRIjBmeIJlmCoh1jIUjs3pjlZwLBQK6X4I7rl+Ff769Hh+8+jwOb+6GIG0Rjm5fi2WHlOgz/XpM6icG8zkxaE9Olf9eeAL04JAlO336dMmKoJGw1HukZ8+e6N27N/r06SM5CckpTqGlPGgXnhznoDUTID9GS2gCd6NgiMrdqoDBMwjBXvnY9MP7+FHMWecnuotFd0jEVVfdjLtm9IW37GxQiJHjob1xxc2X4dhnG7D267exa38+OvRKQKA/ra8QidBAL8cOUFW/CaUuEhNve0hYFhp8u3YXFn68CqUqTwQER6Df5Btxz11TER9gbJT/ouoivOF2AuSTGDRokOT0Juc3NTk5dpOlh0ueVoQFw+23iC/YDATIsm5XgmG1WaXxDl4hg3DL3CugOroD+1NtiOnRC3379Ed/MdLbr3KkdwVv0SQl5nsaft2j8O8yGlu3bcNRk4ijUyOk+2TceY8QmqFRdfgfFDCGDcKtjz+NbiPWY+Mfu5GnC0OnhF4YNGwwEqPEdNtOTjzYDPefk2wCAWpqchzw55gcOQtJLGgCSA5MoLUToI4e8piMC1kWN1kYouFINElZLQpovMLQe9Q0jLp6hlBM0WQgKu3aXTkivjEUvUZdJj5TKYmKJgb/Ebhz7ggnuCmg8++EUZeJz1ThcBcVSO3XciI5jtIqCNCDRU5vmrTNcY6rVlEAziQTqCRAk5jSGCT6PZNoXOjgJsEQxay0MBSiG63oISYCjadoSPFFZd+U2p7FoiGwOS4TYAItgABZ0tTkSr0C25RgkPlPfYVrDkqoNWJxnAixMI53MLy0DVKKmpO8wHt5HMYFvgF8eSbQDgjIPjhqYqXJOi90cJmFQQWrdRpehQZeod1xye23obN6EKI8m2IqXGhkFden6Snk9R9aRo44F0yACbQ1Ai1tyQSXCUbdN0oFg28cxl57N8bWHZGPMoEmE5Cd3STqLcGMb3KBmpAAvcTVbvk3IWEXn0odGWp94XTxtZqaHPnG3BVogTbqGUgtGm3KwqA2NlrLgAJ1afzwww/dxbTqOvLqVFU7atggJ5K8+p18mBZAon2y+UdrN7SGh0zOP/+tToAqH1rpkH6HSUlJTfottubfAU0PT5Xb7t278cknn1SH1EzfiL3MjCo6+VmrqwWCltSl1Sqp2WXJkiUuyRnlw3GqIjlfDbmA3DNJTov+Ul73798vOaPrSouc1XKdYr9d1zn2x2gNGLqHxIVefkg0LnRwmYVBXnx5jQJaRe3111+XmmxoaUF6y6M+xBSHvjdXoB4x8g+0tmvQNMF00+UbSfEiIiKkwWDyPloUiX7sFKhbJr350Hfq3y+/sco/JCkS/9OiCNBvjdbRoHu1efPmJlVC9KC3pEC/RaoM7QNVYI75lC0LWgN9y5Yt0sf+HHmbKlFnKlJ6u3XmDZfiyE21lCfKm/ysOFoQFJcqQXquKA/Hjh3Dgw8+WO3ZlPPZ0L/EiF4O7YP8TNNzLm/bH69pm35LFF9OiwaJ0ufll18+7z44nm9fz9hvO8ar7TtxpHtHLz70UuvIr7bzmnO/ywSD3uiGDBmC33//XVrn+t///re01CZN40BCQT8OUkz7tZZpf32qST82V/oLaCEeCrSSmzwQZpsY41FbIBGifNIPjHosyMuHyiJY23m8/8ISoIeclm+Vf2+NzQ293bWkQOWij32gCozKah/oxclRROyPy9tkgThTeVLlRRV7fYFWQCSxpkDPCD0v9JzJImJ/Pu2T49L+pt4r+7Tr2pZ/G3XFqesYvfQuXbq0riguOSZbayQ2JBjubAqrrQAuEwz7C9BbxYwZM+x3nbdNAkKVt+PSm44R6cdGbx6utkwOHDhQZS04XtPxOy3YQw+L/KZExylf9t8dz+HvF44APVizZs2S1guvbVZbqswc7x+9mDjuq6kUVAk6E8/+paSmdOz3UZOuY6Va00sJ/Q4dK256PtpyoAreUdTobZsq0voCnevY6kD7SGQbEzIyMiTBJt+CM4FeOBx/K3RfHUNNVh7to3tNwkHN7c68ADim6+rvzSIYzmSSYNC62PSpL/Tr16++KG45Tu2JEyZMkN6EqFKq6Sa7JSN8kToJUL91WpK1rkDi4BhoFT/Hh9sxDn2nVf4cK/ea4h0+fPi8yr2meLSPXp4chaClODpry7O79lOF6Tj9CwkINSXXF+gZldeTl+PSvsYO6KRVHunagwcPrrdJiq5HzfNyS4Z8fXo5cNxHYkDltA/UskFLFdN69/QC3rFjR/vDF2TbZYJBABx/8BekRG66KD/MbgLdTJepaSp+mrjQmdC3b19nonGcNkigvpaTNljkakWqLmnVDjXsC5lZ8oRvDTuzdcamN4f2JJCt8y5xrpkAE3AlAZcJhiszxWkxASbABJhAyyPAgtHy7gnniAkwASbQIgmwYLTI28KZYgJMgAm0PALtQDDEKn+p+7Dlz11IyS6V1uRoebeBc8QEmAATaPkEWrBg2GAxFSL1cBKOpuXj/J7LzsG1lp7C0vmP49Zb7sE7Kw6jyHThZ3x0LucciwkwASbQsgi0XMGwWVCS+Rc++fejePbjzciz1rx6d604rSYU5Z/FwU3f4ZMFm3DowCas3JiEgjIxYKvWk+o/QAOGaOAPD9yrnxXHYAJMoG0RcNk4DJdjsZlRnJ6E9es243DaaGQ9Oh4Bzi6pai1C8o71WLN1G5Yv+BSbzxbBJFSivLgEZWKVv6YEHx8faeBOTYNvmpIun8sEmAATaOkE3CQY1LxUgpyMdORZfBDoY0OemG8mN68QZpUnAoNDEBzoA7260uARq/OV5KbhwL7DOCssAmt5Ovbt3AePhHiE+2hgyj+NoydzYAwMgrYsF1k5eSgs1yIktiNiAsV0AWUnsPC1f+PVDeliXXAjunWNxb7dh50axdvSbxjnjwkwASZwoQi4STAsKDy7Hz+9/iKWZHfD2B5m/LV+E/7afxxFhk4YPv4SzLh6Okb3jIRRI5p7zGJI/Pbv8Mxzn2N3Vh6Uez/G3TfswgPzP8FDFwUhZfNHmP3P3xEzahS8zuzCFiEmyflBuPbZD/H89T1g0Aaj3+QZmD3AGwm9ByO+dCGmXvcqFMLKoOYo+lSfvu1C4efrMgEmwARaDwH3CIbNhNK8k9i15g8s2rUQy739EOjrDaPBCFXxMaz48gVs3XMKL73+BCYl+gkfgRJ6sZRrVGQIfI9lwaT3RnBkFPyNwgKxWpBxdBd27fwDa3fsQGB4GPy9jQgJ9YGnUQOl8C9AFYgRs+ZihHQfbMhav1gSCBtNGNgkD0brubGcUybABJiAqwm4RzCqcq2AwScEfSbejPtun45hvWKgztmNBa89g1e++wZvvDcYvV+cjgi9AZH9rsbT89Lxx65XoJ/wf1j4wQ2IMahhMxcLQREWglj21Se0N2568j+46/L+CPMxQKcXglF1rRo2xFTpHJgAE2ACTKBxBOqsXxuXZF1nqeEXNgz3Pv4orhrbC5EBvgiNG4Rr7r4N4yIV2LXkB/x54tyc+1ZajEUsR6DSGWDUqqqakZRitkmVygP9Zj2BJ24bg7gQbxjqEAsrC0VdN4WPMQEmwAScIuBmwVBAqfGFr7dYulDOnlIHr/B+GDksGObcv7H/mFhroPKYTTi/LeKLQvSOqoovtpSiyUr8IyyMYHiqzh2Rkzz/r5zi+Ud4DxNgAkyACThHwG2CQb4DqdoW4ysspAJ2QUgANFoN1EIIzKZz4ySUKjV0KuG2EIPt7IfbKVUi2yIJk9m5PrJVaxyI+ebtpccuC05vyuMwnD6BIzIBJsAE2ggBtwkG8bJRE1NxKg4fTpUG0FmFA7u8JBenj2/DHzsyoA6IR7c4/wo/hLAgVGIhHB+9EuVFhSixEweFQrheRDMTrdrnTJAFg4SG7BFnbJLa0qW1fVvCUom15Y/3MwEmwASai4D7nN7CIrBazMhK/RPzn3oGmuKbMThGi8yjO7Hs28+w6CDQ76ZZGJVgkMpKPaV0AeGI9dVi45Ft2PDnUKgTIhHopxcrU1GVXyyaq5zr80Sjsql/lEKM0ibjhAMTYAJMgAk0nIAbBUNU2aIFiayMnEOL8Pj136C43Aa9WJfX6OmHHlMewL/nTEKwuvL9X6mBV9RAXDqlOzZ/sQgPTFuFnhfPxquvzYZeOMENHkYx4lq0VzkRbEJ8DDotjB4G0ezVFPvCiYtxFCbABJhAGyXgNsGwCd+FzaZAQPRo3Hr7QGRs+h1/HrOh69AxGD9xMqaMH4hwL/vsKKH1iMWMJ95FcK+F+GXxEuwpKUKZWYWYriNwycRidOsXVXc32sqb5hs3BFMn7IfH8C7wtutt1UbvKReLCTABJtAsBOxr6Ga5QEWioulINB9ZrQrofOIwcdajGPXIP8V30UwkOaJruTQ1S/l2xIRZD4nPg9LU5NLAvIhr8c6Ca2s5yXG3AsYO4/Hc5+MdD/B3JsAEmAATaAABNwmGyJFojxI+bhHUwgdBf0XfKMkXQdvOBOpO60w8jsMEmAATYALNQcCNLmAllDrRTVavg5Ouh+YoL6fJBJgAE2ACjSTgHgtDoYVnUAJGXTkJBs0QRHk556xuZJn4NCbABJgAE2gGAu4RDNEM5R3aBzc+9S5ubIZCcJJMgAkwASbQ/ARcJhg01sFsrlhIlQbU5eTkNH/uHa6gEnNM0Wp4dQU5jn08JTne7c7j0dx1EeRjTIAJtFcCLhOM3Nxc7Nq1S+KYlJSEiIgIaRlT+6VMSUjkUdfNATwhIQFeXl51Jh0fHw8/P5pC/ZywJCYmIiAgQDjhK1w6Q4cOhUGMMqdAAkOBjpWVlTVr/qUL8T9MgAkwgRZKwGWC4e/vj/79+2PLli2SWMyePRuZmZk4ePAgCgvFynrC+khPT5f2ySwqutrWPx+UvejI59b099ixYzXtrrZv9+7d0ndp9LewiuoLPXr0kKYC8RADDGNiYnDmzBmnpySpL20+zgSYABNoTQRcJhj2haY3+Mcee8x+13nbJpMJVMGfPHnyvGP2O8gqoUo+Ly/PfneTt7du3YrycjF3uhOBLCZaw3vv3r3w9PRkK8MJZhyFCTCBtkegWQTDGUwajQbUPESf+sKkSZPqi+KW48nJybj33nuxfv16t1yPL8IEmAATaEkE3DgOoyUVu+l5sfeBND01ToEJMAEm0PIJuEwwyEdRUlLS8kvsohySb8PHx8dFqXEyTIAJMIGWT8BlgtHyi8o5ZAJMgAkwgaYQYMFoCj0+lwkwASbQjgiwYLSjm81FZQJMgAk0hQALRlPo8blMgAkwgXZE4IJ1q3UPYxvyTmzBbz9+jx9+WY1DxSEYOGICZt50HUZ1DYJezXrpnvvAV2ECTKAtEGi5giFW6CvJ3oevXnkPKQk34eFZ/eHZoAUxLEjZ/B4euvcVrDh0GsWl5WIN8H04+vdG/PLrOjz93nzcNDwSRg2LRlv4IXMZmAATaH4CLbe2tJlReGoHfvn2J3z95SakWWwNolGevhLPzXkBy4/bMPrWV7F44x4c+HszPn3sEnhmrsfHX6xASkEp6p8cpEGX5chMgAkwgTZLoMVaGDTPlKW0GPmlJjEDoBINW0HDipRty7DsYBHipjyH/zx2LTr7e0AtEgm7fgYWfb0By7bsx6lCE+L8xMSC5+YhrPdGy3NQ0eSENKstBybABJhAeyHgphrPgqKzh7H8qw+woWQoLh9kwh+//Y4N25OQ79Edk6dfjWuuGIMOPhXZsZqKcXzjB3ho7iv4MyMXyu2vYOqIdZj94n9x14ggnN76MR59YS26Tr0Uvil/YOWGLUjKCMBV//cqHruiK/QqG3IzUlFs0mDk4L6I9jVCI/krbCjLPoOMEhOMYQbhw1CIWWsbd6tppDeP9m4cOz6LCTCB1knATYJhQlH2Iaz79kd8vP9TfKEBzOVlKBV+BZtqP/bvWIllGx/Bf1/+B7r7U5ZssFnKhN/BCpVYCLwkLwNpZ3KQVyziW8uRuncNlq34Fb+uXwaF1YSy0lKYDdE4lVVaOTGgComXPoa39TPRcVw3scpfhX1Snrkd7776Af46q8bY20ahk7e+gZZL67zJnGsmwASYgCsIuEcwRPOSzWpGeZkJJeUWBCVejFtuvgoj+8ZBk/UXvnnrNXy9+C28kNATbz80HN4aI2KG3IRXnsrBjH+8A9XIx/HBS9ehe1QIFCiHWcx0axLTkOSX++PyB57E3dMHItzPC0HhkVU9nwzBPXDJ9K5Q6XRQKWwoSd+Mtx57GG8tPYnoCQ/h/uv6w99DK9LjwASYABNgAs4QcI9gVOVEjYDIYZjz7Au4YUgojDphapRHwU+bh8O3/gfrvlmAbdcMxrhIDdRaT/h5G2AxK+DpF4GOHcLho1HAai6HUvg01GpvDLrx33hx3kzRlCX8CSqHJiKFCjo9WRZW5Bxeghce/T98uuYkwkfNxnNP3Yp+UT4QyXFgAkyACTABJwm4uZeUEhpDGOLiQuFt0EEtVrFT630RmTgaE4cHozBtM3YezBENUhWBHMwm0Y1JIVa9ExpRGUgYhBAolAiJ74YOAR6Sf6JGf4LoaZWy5VPMufV+fLQ6HV0vexyvv3AvRicEw8BjMGSg/JcJMAEm4BQBt1kYJAKSEIjKXlnN06wQzUa+CA71hNqSh9x84YcQcenln5ZFJSvAZrFW6/6qIvUQ+63inyodcSyurQQHlr2FRx75Hzam6TD29hfx2N2XonukH3TC2c2BCTABJsAEGkbAZYJB1kCpcD7XHsiPIbrKmnKRkyfWxkal/0AM0CsrOIkD+7NhM0QiJtxXEgGb6OtK/gcvnUI4yE0wy2aHuIBCKSwM8d0ihKTmYMWJtfPxwJy3sCU3DFc//hTmXDsScSFeaKpWnD59WlrbW6/XV60BXnMeeC8TYAJMoG0RqPUFvaHFpHET9Kk1iENWiwk5aRvx1n/ewqqkDBQV5eD43rX44o1X8OXWHMSOmIExiR5SEtTEpPENQJhBJab3OIzkzOIqK0MpmqNgK4VF9KCq6YrW0v34/o0vsCXDG9MefBZzrx+BKF8tLKJnVrlwmAvdanSgJWOpnGT9cGACTIAJtCcCLrMw6oUm9ZSyoTQvE7uXvYmbxVgKGgdhMVV0r/XreTXmzb0SHTwrusBCqYFnZH+MGRKOP5Z+gOtGr8PIabdi3sMzJKe3EhZR8ddc84tUUSLW4C4pPINf37gLGz7QVOsNpdB7IyQ4BKGRiZh8812YMSQGHtrK69ZbEI7ABJgAE2ifBNwmGDbR9GQTLUgBkYMxaVIc0reux+5TNsT1HYYRoy/ClEsnY1BCoF3PJdHLySce1/3fi9B2+hnLV2/CX9v3IbN4BjrF9kK/fsfQOyG0Rh+GQtcFVz3yAI7jXfyyMxNFNiVKTWoEBgXAS3SlVQq7JD/jONJO5iFu3DUoHxAtBKN9/gC41EyACTABZwm4STBEcxX9Jypug383zLj3MfTQ5CGnyAZPf3/4+frBz8cTjvMAKtUGhHYdjZse7IXLbsxCvtVb+CEM0AVch/99PgWGkKgaBQMKAzqNuAHPdByHe3OpG67wd1gVopst9cwih7dNNI+ZYRIi4h8ZLXpssXXh7A+G4zEBJtB+CbhJMARgYV4IlwMUag/4BYeLij9GCIj4Xk+HJaVKD5+AMOlTdZu0gYjtHFj1taYNld4HEXHiU9NB3scEmAATYAINJuA2zy11jRV6IfVwksdU1CcWDS4Nn8AEmAATYALNRsBNFoYGBt8Y9BzeGwWG7gj1cJtONRs4TpgJMAEm0N4IuEwwaBxGiZjfibqb6sT4iWpBoYZPWB9cL2aTnaoMQmQr9hmUlZWJ8R8WaDQa7lpb7SbzFybABNo6AZcKBlWkJBjnT9MhBuGJuaFCY+MR2sqJ2o/DOL+crbxwnH0mwASYQB0EXCYY5eXlyMrKAlkax48fx6BBg+q4bPMcio2NhaenZ52Jx8XFwcfHp5qo0T5fX9+qfb169QKN5ObABJgAE2AC5wi4TDBo9Tm5sqbKNiEhAXl5eTh16pTUVEVv5iQoZ8+ePXd1F28dPHiw3mYiWilPJSYztA/y6nmyxeDh4VEVp3PnzlITm9FoREBAgBidXmR/Km8zASbABNoNAZcJhuy7oL+BgYH417/+Jc25VFhYCLPZLE2nUSxGX5MPgALto3mZMjMz64RNQkMWC6XjynD48GExDkMs/1oZ7Kc2KSgokHcjKSkJKSkpUn69vb2Rm5tbdYw3mAATYALtiYDLBMMeGjmEqZmnrkAVNL2t1z1hoRi+IeLl5+dXq9zrStfZY9nZYrLDWqYWcUyDRIIEjs4hISTh48AEmAATaG8EmkUwnIFIzT/UhCU3Y9V1TlBQUF2H3XYsOTkZzz//vNuuxxdiAkyACbQkAjwgoiXdDc4LE2ACTKAFE3CZYJBvIiMjA+Qcjo6ObsFFdk3WtFoxiSFPce4amJwKE2ACrYKAywSD2vjJH0GVqJeXV6sofFMySeWUe1U1JR0+lwkwASbQWgi4TDBaS4E5n0yACTABJtA4AiwYjePGZzEBJsAE2h2BC9ZLyi2kbSZkHNmOjRs3Y8eufUgt9UfX3gMwYuwo9O0YJFb8Y710y33gizABJtAmCLRgwbCivCAF635cgoyoi3DFmM4wNKR+t+Zj79KP8fo7P2LH4VPIyMpBkUULv9VLsfCX0Zj9+FxcOTgaRsdVm9rEbeVCMAEmwARcT6DlCoZYbakobQcWvPs2DnUxYuSoToiSVstzBoINp3d8i+dfeAdrkzXoOeISXNZDrKynLEX6gc34delC/PetWHSJvQP9IrwglhbnwASYABNgAvUQcJlg0KSD8rQf9VzTqcO0Bnh5/hkkp6Qj3SsHpdKobCdrdksaVn/xJVbuL8GwW+bhwRvGoluHIBhUJuSkDIQq7T58tHEhth6aiR4hnlBrnEzXLuc0rYizI8XtTuNNJsAEmECrJeAywaDKk+Z9qjlYUZqfjl3rlmFfeVcMjbdg/7bt2HvwBIoNsRg4fCRGDumBYGPFpIBWixjTsf93/G/+AiTlF6H8+EI883AxZt5+Jy5O9EHu4ZX49Ls9iBoyGJ6Z+/HX3iScyPXGyGtvw1VDoqGxmVFWrkR0vytw6y2XYXC8f9V64ZqwIHjp1LCU5aOotGKOK7EOYM3ZrmMvlZVEkgMTYAJMoL0QcJlg1A3MjKLsA1j28dv45pgekYE2nE1NR0Z2HkxqH6xc8TvWXzEbc++4GNGeQjSsZhScPoAt2w8hu7BUzCO1A0sXq5A46XpMijfi1I5FeO/dJdD/+jO0xWdxOjML+dYQKHpPwxWDIqFRBWHkzY8itDwWQzv6oMK3bUV+6l9Y/MV8/LT7DPzir0aPWG9o2PFd963jo0yACTCBSgLuEQzRvGQuzcOZk+k4fCAPebG9MGL4VFzaIRiqwpPYunoFFn74JvwiYjFvRjfRdKRDcJexuG7GLhx4czEQfyluu/kKXNTVT9gCVhTlZCAj7STy0osxYPJluH56LPy8g9B7CImF8IwrjOg4aBI62t1mS+EBLHj+33h3yZ/Yn+eP6+6/An2iPKssD7uovMkEmAATYAI1EHCPYFRdWAnf4ERMn/047pjSDzFhvlAWpuCPjjo88dQC/PTZQkwdF49+gWp4h3fH2OHd8Z+3lsEzYRJuEYIRqVMK46NYjCZXQKnyRKeR12HeE/dgdLdIeOk1UAlrofbGJYsYiV6G0nKzlMbR3Ttx5HQ/BMZpoW1I76uqsvAGE2ACTKB9EXBzVamGwTcB4yaNRY+4UHgb9PAMjMWACVdgfC9vpO1dhe1HC2GrvAdWixkmM6AU8zZpq7oyKaBQqqAU64R3Hn0ZJg3oCD9PHdR1igWgMnbAJXfNw//9cw6uHxGMgys+wvs/b8PZ4vKq67WvW8+lZQJMgAk0jIBbBYOEQKEyQK+rcG5LWVWooPeJRkK8L1B6Gqlnzi2URHM1UU9am1WWkIrCqWjSP3FAY/So0Tqwmk5j/Tfv4csVScg3WSoEQemFjv3GYuYt9+OR+69CvCYLfy7fjtTCctTmqm8YSo7NBJgAE2jbBNzWJGUT1Tb1pLKai1BUQivdaSvJWmEuy0ZmRgkUWh/4elWupU3NTsKyMIourxZhZpjtNIMsDFIBk6XmXkq24uNY/un/sBhp6ND1EQyJEEuuVrZVKXVeCAzwEs5uBcyia6yZezq17V84l44JMAGXEXCZhVFeXi6tjEdWQY2zuIoK3iYG4xVn7cbP3yzG3tR8MW6jCBkn9mHNz19j0dYsBCWOxuAEn0o/hLAgPH0QpFei6EwqMvLLqpqOFGRhiGk/rCI9Ox2pgqLU+CHID0je/hM++3oF9h5LR25BIfLOpiJpy2J89P4POFigReLA7ggz6tAYCDQ7L3errULOG0yACbQDAi6zMKgCpSVXaXnWGgWDLAwxdiE/6wiWffYScg4uRbi3EiW5YnDeoQNIN/bFjbddg57BFVlSKNUwhiWgX7wf9uz7Ec/MzcXocZMwbepAaQp1BURTUi3WgcIYh4mzpuGXPR9i6ccvIPXPWAT5GMRC4sXIST+Gv/enIbjvFbhh+kCEeGgaJRg0DoMH7rWDJ4SLyASYQBUBlwlGVYq1bNhE5U71u6dPjJiSw4gTW37HxmwrgmLi0CVhLKZMuQ7XT06Ep9x2JHwbxqCemH7njUj/YjX2bfoZJzO16Dd6AEKDY9AhtpPoZSVbI44X1YoeVDdj7oNWfL34D+wT04FsScmGyjcUUTFioODUyZh61TW4uFcY9DyXlCM8/s4EmAATqJGAmwSDPBhW8UaugEfwANz44PXwPr0fR8/5POMrAAAN/ElEQVQA4fEJ6JqQiMQuUfAW3WbPBQVUugD0n3oXnuw4HHv//hsp5k4I99QiqOdUzH28C8KHR9dqHai9Oggr40F07ncR/j5wCIePnIEqIBodO3dGQtcExIb7Cod57Z1wz+WDt5gAE2ACTIAIuEkwxJXI4W0RfgmvQMT3H4tRYRNoVy3NV/LNEaKhD0CXfqOlD/krpCrepy+uurGvHKnWv0qdHzr1GSV9ao3EB5gAE2ACTMApAm4TDPJfSL1jxfgJldSrlpzjTuWxKlIDo1edxxtMgAkwASbQdAJuEgwltEZ/hHeKQoxnFHxFzycOTIAJMAEm0LoIuEcwFFp4hfTCtHvuRx9Vd0QZWTBa18+Ec8sEmAATcKEPg7qY0lgMvV6PwMBAB7ZK6L0jMHDy1RjocKS1fuX1MFrrneN8MwEm0FgCLrMwaBAbCQaFU6dO4cknn2xsnhp9XkhIiCRYdSUgx7EfK0L7jEZjlQM+MlLMeivGk9QVWDDqosPHmAATaIsEXCYYMhwa0HbmzBkcO3YMJSUlyMsTa15Urk5HA/voe3OFsLAw6HS6OpMn64esIHvBCA4OriYY0dHRYjLDCjTh4eHStlZMU6IUI8xduapgnRnlg0yACTCBFkbA5YJBFeuAAQMwevRoFBQUIC0tTapkSUhycnKqBIMskvz8fBQWnptssCY21NSVnZ1dZb3UFKch++i6xcXFyMzMrFoh8OjRo7UmQSJEIkdiERQUJOW51sh8gAkwASbQhgm4XDCoYqW3+IkTJ9aJjSpuqrRJDOoKJBgpKSlSJV9XvIYeI5EgEXMmnDx5UhIsanI7ePCgM6dwHCbABJhAmyPgcsFwlhAJC/kO6FNfSExMrC+KW44nJydj8+bNOHv2rFuuxxdhAkyACbQkAty/tSXdDc4LE2ACTKAFE2DBaODN8fX1lXpQ8fTmDQTH0ZkAE2j1BFgwGngLqQnNYDBIPg1nfSANvARHZwJMgAm0SAIsGC3ytnCmmAATYAItjwALRsu7J5wjJsAEmECLJNCOBMOK7ONbsPCbH7Bh/xmU2S8S3iJvDWeKCTABJtCyCLRgwbDBUpaDg1s3YcfhszA1kZulIBlL3v8PHp07Fy9/swVnS8prXA+8iZfh05kAE2ACbZZAyxUMmwVFZ3bis+f/hZc+/gM5Flo+qZHBVowjG7/CRwv+wPEzJ5C0+yiySs1iDUAOTIAJMAEm4CyBCzZwr94M2swozTyC7dt243DeEeSK1ZeC5fW+6z3ZPoIN+Sf+wCfvfIt9xQp4qpXIT81EbpmFLQx7TLzNBJgAE6iHgJsEwwZzmZhX6uhBnLaEoEOwFWfEdB/pGTkwafwRHdsRcTEh8NBUGjzCuig4fRAb129Hqmg6MhUcwOrFa2EdMhjxIXqUnj2CbXvS4RcTDU3hGaSln0F2iR4d+w5Czxhf2OuKueAEln/2P3y7JRedRoyEZsta7Mg+i7wSYWFUrflaD6UaDtM4DJq2hAMTYAJMoL0QcJNgWFCYuR+L/vsMfjkTh0FdLEjasRNJR0+hRBeNfsPGYOrM6zB1ZAJ8tUpYzaU4/fdSvPPeLziUUwDbge/x1KPHkTf/E8wdH4SUrV9g3rylCBWTHHqcTcKepCNILQrGNf/5GC/N6gmDsCIo2Ex52LfyI8z/bBMQPRX3zJmKnfdvx+7MIpSU2mCjNilpuVgpulP/0JQmFGheKZoPiwMTYAJMoL0QcI9g2EwoK0xD0pZdWL1nBbb5hyMyMhSB0V2gMOXj75WfYO+hTKhefBpXDQ6FSqmCZ3AcenaPw+7kHJj9YtC9X290CNQCVguyTiQhad9ObN53GFFdOiE6vAv6eIYjJsRTnFu58retDOl7FuOt175GkrUzbp8zG5N7WXFICBIsJpidnHiwvfwQuJxMgAkwgfoIuEcwqnKhgIdvJAZPm417brwE/RMiocrbj4XvPIcXP1mM9z4ciqE9ZyHWqEdotymYc+dh/LbmAAyj7seH789CtEENm7lYrGUB8dEiKG4w7njyX7hxQk8EeenEWhgaVMiFRXSh3YRPXnsLvx7SYNQdc3H7lO7w0vwtmpEoMzZhHYh/uUWp6s7wBhNgAkygPgJuFgy1WNt7IG65905c0s2zonL36YXLb74J29f+hZ/WLMKWYzMQ291DyrfVYhZNP4CnTg+DViXFpzpeqVJBpTKi91VzcP/MIfCyd1qI47ayNCx7+yW88/MuWKMmoFtEEbat+BU7TMeQlF0CU1k6tq9aDNXRYETEJaJX92h469SVYlMfMj7OBJgAE2ifBNwqGDZRJSvVPvD21J6rnJU6eIT0wOCBgfhuwSEcPJkPW6VgkFO5wgiobGaS7pFIQyGalUTTk0dAAIwOYkFRLCUnsGPzERSKnlYFp9bj9blLUFBstbMozuDNR4RfQxGMwTMew/w3bkHvUG+o7S/TPn8PXGomwASYQK0E3CYYctVvs5rEkq32zmIhCaJXlNWqEFaDhnSgKijVGuiFU9pqMsN+qSOyMEhJzBb7dKpOg9qzMybPuhLJnptxulB0nxVtWJSszVyAk2IBpNOmAMQnRMFb74X4jmJ5VnWF9XIuBd5iAkyACTABRwJuEwy6sE04mssLj+OvHQcwKKQrAgwKlBVl4+judVi7PROG0FHoGedXUbkL5dAYPeBrUCIvPxeFpUIyPCqyqxBOceriVKvjWh2CsXe+gJE3l6DcIsRCpYRSpGrNW4eHLroFX+VfhKc/ex4TOvmLpi5ttW64joAcvzuuB+54nL8zASbABNoqAfcJhmheIp9EVtpOfPzSM7BmXYleYWrkpCRhw9KFWJ3mhdF3zsKwjjqJtUKhhi4wGvHBBiw7tAELF3XG6F5dhUUQJKwQshdKpG6tFU1WNd0eBdQ6I+wLaBbCUZG4BlqdFrT+eA0tWjUlVrUvIiJCWg+jagdvMAEmwATaCQH7+rR5i0z+CNHspFZrYTm7Fe88sRy5RcKh7esDv4BQDL3qQcy7YzQCZEeCUg2PiP6YeuVg7Px8C16fsx2/jLkdr71xL7w8fODj6wdPjwpxcTrjKuEv8THCVwwW9Kh0ojt9LkdkAkyACbRzAm4TDBv5KYQ54BcxAnfcPxoFO9ZgRzLQeeBQjBo9DmOG9UaoZ6UFIN0UBbTGSEx54DUE9fgdK1auxj6TVlgXKgQnjsVVM9SIHxgtmpqcD0qPWIydcSV0GI2OfvoGWxfOX4ljMgEmwATaHgE3CYawLiotDK1XNEZOuwujZt8rjYVQCF+FnZ+7OmHRG0rrHY0R0+4Qn9slwZGao0Iuw3P/u6x6XCe+KTURuPi+53CxE3E5ChNgAkyACVQn4CbBEBcVTmoaLEe+CfJZiy1UzrJRPUe1fqPutLUe5ANMgAkwASbQzAQa0qLThKwIK0KphcHLCE9vL6mrbBMS41OZABNgAkzgAhBwj4UhpvHwCk7ERdddIZzawxHtJZkYF6C4fEkmwASYABNoLAGXCQbN4mo0GiVfxfmzuIrJBIO64coHX8CVjc1pCzlPntKcpzdvITeEs8EEmIDbCLhMMEgswsLCkJeXhxSx1sXOnTvPK4Q8NbjjAaqEFdLYCscjzn+ntHU6nfCL1N3KRmMvHOPQPvvrO36Xc1FcXIycnBxYxADEzMxMlJaWyof4LxNgAkygzRNwmWDQ+hD5+fmSYHz55ZeYP39+NXhUIdMo6ZoCWSSOlbhKTP8hx6dtOdhvU8UtBzo/ODhYEg2TqWIFcHsRkONRHBI3++uFhIRIg/jkODQ4T60+H01ZWRlWrVqF3NxcGAwGyZqSz+G/TIAJMIG2TuD8WrGRJaYmGnoDp0qa3sIdA1kRJSUljrtr/E5p+Pr6omvXrlJ6/v7+Ujza7+PjI21TemTNyCEpKUlKPzs7G6dOnaq3Mqf0axIUOb2a/lJ8+pAFEhMTAw+Pill1a4rL+5gAE2ACbY2AywQjMDAQY8aMQUZGhtRcQxU6fch6kC0B2pbf/ukYvbFToG25eYfi0HcSnQ0bNjSZt2xJkEUgB41GU6MFIR+nv3I+7PfReSQY3t7eUn7lctnH4W0mwASYQFsl4DLBSExMxK+//lrFiSrTgoICqWI9KGaIpUAWhuzbILHYvXu3tJ+sk+PHj0tCQVaKKwM1P1El37Fjx6pmqKioKHTq1KnOOaHIR0H5KioqkuKR8ND2kSNHkJaWhtmzZ6Nz586uzCqnxQSYABNo0QRcJhiOpSRfAzX7UAgNDa06PGnSpKpt3mACTIAJMIHWQ6DuLkWtpxycUybABJgAE2hmAiwYzQyYk2cCTIAJtBUCLBht5U5yOZgAE2ACzUyABaOZAXPyTIAJMIG2QoAFo63cSS4HE2ACTKCZCbBgNDNgTp4JMAEm0FYIsGC0lTvJ5WACTIAJNDMBFoxmBszJMwEmwATaCgEWjLZyJ7kcTIAJMIFmJsCC0cyAOXkmwASYQFshwILRVu4kl4MJMAEm0MwEWDCaGTAnzwSYABNoKwQUYipxm1wYmtWVAxNgAkyACbQdAnZVfJMLxRZGkxFyAkyACTCB9kGg2vTm8+bNw6ZNm0BLlNJiSByYABNgAkyg9RFYs2YNUlNTMWzYMJdmvlqTlEtT5sSYABNgAkygTRHgJqk2dTu5MEyACTCB5iPAgtF8bDllJsAEmECbIsCC0aZuJxeGCTABJtB8BFgwmo8tp8wEmAATaFMEWDDa1O3kwjABJsAEmo8AC0bzseWUmQATYAJtigALRpu6nVwYJsAEmEDzEWDBaD62nDITYAJMoE0R+H+VGenyTXBRAQAAAABJRU5ErkJggg=="
- }
- },
- "cell_type": "markdown",
- "id": "d2279bda",
- "metadata": {},
- "source": [
- ""
- ]
- },
- {
- "attachments": {
- "elements.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlQAAAB7CAYAAACy/R7jAAABPmlDQ1BJQ0MgUHJvZmlsZQAAKJFjYGDiSSwoyGFhYGDIzSspCnJ3UoiIjFJgf8bAxMDPwAnEMonJxQWOAQE+QCUMMBoVfLvGwAiiL+uCzLp9qneX98mX6xNmXItjMGSOxVSPArhSUouTgfQfII5PLigqYWBgjAGylctLCkDsBiBbpAjoKCB7CoidDmGvALGTIOw9YDUhQc5A9gUgWyA5IzEFyH4AZOskIYmnI7Gh9oIAq5G5kyEBd5IMSlIrSkC0c35BZVFmekaJgiMwdFIVPPOS9XQUjAyMjBgYQGENUf1ZDByGjGKnEGJFqxgYrOsZGJi+IcSinzEwrLnBwCC4HyGm4cbAIA4Mj33lBYlFiXAHMH5jKU4zNoKweYqA3vzx//9nWQYG9l0MDH+L/v//Pff//79LGBiYbzIwHCgEAGmsXtKRMhyuAAAAYmVYSWZNTQAqAAAACAACARIAAwAAAAEAAQAAh2kABAAAAAEAAAAmAAAAAAADkoYABwAAABIAAABQoAIABAAAAAEAAAJUoAMABAAAAAEAAAB7AAAAAEFTQ0lJAAAAU2NyZWVuc2hvdK1bm9wAAAI9aVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA2LjAuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIgogICAgICAgICAgICB4bWxuczp0aWZmPSJodHRwOi8vbnMuYWRvYmUuY29tL3RpZmYvMS4wLyI+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj4xMjM8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICAgICA8ZXhpZjpVc2VyQ29tbWVudD5TY3JlZW5zaG90PC9leGlmOlVzZXJDb21tZW50PgogICAgICAgICA8ZXhpZjpQaXhlbFhEaW1lbnNpb24+NTk2PC9leGlmOlBpeGVsWERpbWVuc2lvbj4KICAgICAgICAgPHRpZmY6T3JpZW50YXRpb24+MTwvdGlmZjpPcmllbnRhdGlvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+CpRzJcIAAEAASURBVHgB7H0HYJvF+fdPtizJkock770d78SJs/cgOySssEfZq1BKW/ovbYEWCl+hLR0UmrAJIZBF9l7OcKZjx/Hee++p/T0nx4n3wk4s+w4US+977713v1vPPVNgoASeOAIcAY4AR4AjwBHgCHAEBo2A2aCf5A9yBDgCHAGOAEeAI8AR4AgYEeAEFR8IHAGOAEeAI8AR4AhwBH4iAsL2zzPp3/r1642XvL29oVQq29/m3zkCHAGOAEeAI8AR4AiMOQSqqqqQk5NjbPdTTz0FgUDQBQNBex0qjUYDkUjUJRO/wBHgCHAEOAIcAY4AR4AjAKjValhYWHSBgov8ukDCL3AEOAIcAY4AR4AjwBEYGAIdRH7m5ubXn37hhRfw2GOPXf/Nv3AEOAIcAY4AR4AjwBEYiwh8+eWX+Oijj4xNb08rtceiA0HV/sb48eMRFRXV/hL/zhHgCHAEOAIcAY4AR2DMIXD58uU+28xFfn1CxDNwBDgCHAGOAEeAI8AR6B0BTlD1jg+/yxHgCHAEOAIcAY4AR6BPBDhB1SdEPANHgCPAEeAIcAQ4AhyB3hHgBFXv+PC7HAGOAEeAI8AR4AhwBPpEgBNUfULEM3AEOAIcAY4AR4AjwBHoHQFOUPWOD7/LEeAIcAQ4AhwBjgBHoE8EOEHVJ0Q8A0eAI8AR4AhwBDgCHIHeEeAEVe/48LscAY4AR4AjwBHgCHAE+kSAE1R9QsQzcAQ4AhwBjgBHgCPAEegdgR49pff+2K26a0BjWTquxCchv6oZeoEEClc/BAX5w91eihuBc35q/fRoKM9Bdn419FZuCPB1glTYNbL0T30Lf54jwBHgCHAEOAIcgdGBgMkRVJVph/Dp+5/gSGIZmg1yBM+5H8/9/DHcrvSG5VDx2wxNyL20G59vugBtwBq89OIaBNgOHbk2OoYObwVHgCPAEeAIcAQ4Am0ImBhBJYDI2hEernYwj88ngsocltY2sJFawGwoGUj6RpTnZiDpciy02nCU1es5QdU2YqCHTlWLnOQklOidERriDRuJOYaKlr3+mpH0xaCHVlWP8pJiFBeXorpFCLmdA5zc3OBkK4UF514OoLcM0KkbUMmwLKtAVXUThFZK2Du7wNXZHtaSIZ7LA6jZ6MiqR2N5NlIzSgG5B3w8XSCXCTGUy+PowKn7VmibSpGenImyuhZotDroae4bDAYY9PQxE8HWyRO+Ph5wtJWM7jWve3i6vWrQa6Gqr0RRUQnKKirRBBkcHJ3g7OwMhbUYwiHdnLutwoi5aHIElfP4u/GLl+uQkFyCBOk8rL7vdiyIdIN4KCBlE8dYjgACGgQCAZtMNKn0nQtnE0wHtUoNncEMFiIaNLSpjoVFS69pQWXaQbz/6js4pZ2Hdz9+E4sClbA0sZHUuUd7/E2LRWNNPq7GHMauvYdw8nQsMqrF8A0ejxlL7sBdq+Yj3IvabzGqScoe4RnQDZpLLXUlSL5wBLt2H8Lp83FIzqyEpWsgJkydh+WrV2PhtGC4yCUwHwuTaUDg9S+zXlWB89v/iXc/OQ5B1GN49eWHsSDUAaN1evYPlf7mMqAy8Ue8+9v/4UxGORpVKuh0dIDU0R5Afw1CkogseBgvvfIM7pruAREfo9BrmlFdlIqzh3dix/6TuBifggo4IzxqKmbMW4olC6YgxNMOliLzMbE/muQ8MzMj8ZuAjWZG/rSSQABbrKtRVdMIg0ROlLGANsJq1NQ0oFknhI1cAaW9nZGb0nF66aFqrEV1ZQXKK6rQoBZAItWhuKoRKg0RTmwytb2CcSrUzaipKEZhQQ5y8yvRqLOAws0XAd4ecHGUXx84enU9SovKoRba0HvlsJK0nhJ1qgZUVVaiQSWEwsUZcuLumERqa3tpOk5s/RabjyWiCrU4l/wLzPKldgtHI0GhR3NdAS7t/h/eef8rXCijPrOREUeUxkfyMay7eBHZ1X/B688sRZib1RDq8JnEiBhgJfVQN5Qg/sA6vPX2pzhTbICcsLRU2MDQkItT2z5CbEIOav/vFdy/IAwOUhOZFwNEYVizGzQoT96Hb7/Zj7jUTEhkGcgpqYE6mAiq0Tg9hxxMPXIuHcDJK1losJBDbmsHi3aUvYCuuTjIIROz/WfIX25yBRr0LagpiMeeLz7EB58eRrm5LaylMkhRjcTozYg5fAgXHn0Tb/1iBULdbMYEUW+SBBWxj4zjmRhKxmT8o6tF8vEN+PqH82j0moulUQLEHTqIY2cTkd9gi8jZC7Fy7SO4d2EgrK6LaGjDrM7B+UM7sW37Lhw5fQW5NYCduyfsxST2q26Gt0ELOpxQog2hqQKZccexZcMGbNsXg8xaHYTExdII3TBv9f147PH7MS/CCwqpEKqSc1j31sdItojEXY8+gKWTvSETNKMg4QA2fLYFsbU+eOT113B7qO3In5t6DRqqC5EcG4MzJ/bim8+Pod6cUNdp0NTUQie4NoqztT9Gy78GTT2KU47h839/i/MV9lj53Ov4xcML4WcP5J9aj9+8+h+c3nkQlxZFwseJCK3r42q0IDB07dBrGlGSdhT/+/vnOFlsjcUPvYSnH1yMCC8bqCtSsffTv+CDjQexdcckRAR4Ys44BRepDAh+A9R1adj5xTeIzqKDHh0MDVW1qK1thpoWSunIX2UG1NrhyqxqboDWIMWi5/+N1x+dCT+HdsjRviM0F8KcqFNOT+nRQnvnuT1f4l+fH0eD6xK8+tpLuGtOAGy0RTh/eDu+/XoHiisqUNuiod1zbCQTJKiYaI2J49ghgTZy9j/1lkFbh6L0ZFw8cgCXGw/iR0s1ycAlEFswVmMlTm5Pw7kLJbDb+m+s9JcSIUQkUksJTnz5Nt749wFk1aphZiGElQxoqchFZksjGrVyeJFoT08Lkk5VhfSz2/DhO3/H5gvVkNn5YtEdU+ElKcX5IycRs/ltXL2ajd//5f9w53QfSC3EsDBU4OLer1FDy5mNzX0IFyZgy+efYsPuNDjMCCZulmnAr20swdWD/8Mv/+9TJNeBRJxO8HItRmYBYTiKZ4quuZY4UZcRk6+Fz6KX8NZr98DXspVzYrtgCWZ5f4e4pDwUl9ajWW3gBFUva6amsQrZF08hOlOP0FW/xd/efZjmzjUxgIM97r1vJX7cn4ysjEzklddAFaAYOiOTXuo1Wm7ptQ1I2PMpPt+bDK2jF3zMClBaV0cc+iaodNRKzvDrR1dr0NLUDBWpcVjZELdFZgWJRET7B09dECA948LUGOzccgQF4lA89/u38NJq/2tiUCWWPRqKRXf/HM1mMshIL3KsDD/T2NE79aZR2sfIKSKmGLHTmgwQGL9rodZbws17Ph545hnce1s4bFvSse3D3+GPG/bh6x0JWPhyFKwtBCi5sBEfrj+EIkkEHnvlBTy8ehq8bAUoSzmCDf/9CN/uTSMFWiY/16IyKxZ7v/sa2+Oa4L/4Rbzz9otYGGRHbEwduXKIxedvvIr3N/+If/7TF57OT2H2uOn42Qs/Q0HpP7Fn/7dYj2J4GtJw7MBViAJW4bHnf4Z5/jKTmKzmIms4B0zFynv1WO4egcmTg1Cx7Uk8/s+yTj0zun7qiQPX0kKEttga/pPC4d4mniUKvr4wC5llDdBb2MLKqlWHbnS1fmhbYy6SwtFvAuYtEmLOMytvEFOEpUZVg/TEFFQ2q8noxApS2sTMuYiq/x1AXPTqZFp7PtyKzGY/PP7qg9DvWo9tiS1QkR6QhhFUPPWBANtM6lFVoaIDugBi4sA3kypIOal9mNHhWGIpgUTMxuXY0JXtAyxoSBcyM+4CYjJ18JqzliQ/7tARd69WrQVIJcfCQgSRhIhSEpmOJYLUJAmqVv0pxpxqI6ao+40sK+o8oQJhs9bi9Xd/hdUTHI2cKF2zOW5bNhf//SEBSecSUKaZCKlZDc7u243ESgvMfuE5/OyehQh2tjR2vu2UJViRfQmXEwpQQYuVXluJvKQLOH0yDzKPSDz03OOY5WUJdXMT1OzVNmF49Pd/RF7WC/jy3A4cv7QEoe72cI26By+8UITStz/H/s/+hkaDDL6Tl+PJ55/D2lnuJqPUKBDL4R21Br+jD0Nd3ViM3dtap4mOFI1HaxLJPTF17W/xTcgDkAVHgmhwY/s1dcnY+Ld/4XBuA/zXzEVUoBNsuYZqr8NAKHVA8KLn8Omijtm0jXk4suFD/OX9zcioc8K9c2cg3NsBoo7Z+K8eETBAU3sFn73zAfam6zDj6RfwwHJfMp4Qw4x0qnTMUs3IRh4rPIIeger7hr4GpQWNtN6rcHn3h3j+m3SkpJVC5BqBhaTS8eC9SzEl2BVWY94AxYCmmjIjN7mC9KbmTfRE84VNeO/77dh5PA1C12BMmbUQy9eswqxQV9JbHjtWpqZJUHVH8xJBJaCPmVAGWwcf+PsS9+gaaWwmFEFq7wxP6tjLeeWo0zKLjSKkx1VBKw5CWIgX7GzF7UqlsthJxIzJs0iHqqmOzLyLyJkoEVaVe/CrZX74TReym8SCWiK+4EAmy3mobgiBi7UMwbc9gIcTkohTVYXEZn9Mv+0e3L00BFbtlB37nukjN8d1BuHIreLgayawgJWdNybN8TIS7ALGTalNwmevv4A/fXcJorDH8eJTKxDhKR8TCpeDB7KnJ3WI30x6aW/tRWZpDfyXP4ll88fDy46TUz0h1vG6gaysSnDwwzfw7wOFcJv/K7z8+AIEOlUgxriatZr8Xzeq6fgw/9UeAZrbqqJ4nEuogqaF8Duww3iXuUxAzTF8mXIep06ewYu/+SUeWRoK27bNpX0ZY+a7AS0kwq+oKEIDuUu4uuUtPPDeFaRVtRilRkhPRezJXfj66+/x1O/fxst3T4GHYmy4mTB5xvqNDZ2IKTNSFrzm6oDmR4dkZk5sSGqtnliSTMmc+c5QNzP2rt5IiHWkj1qJM8b0YhOKmc1qiG+u1plBbKmAk6sr3Onj7OQABwcHKJVy2JI/LFuSu3tHzEBUmA8UVha0pBlQn38VF+OyUVRZR/5hsnAl5iiiLxWSomiH6pncDxOv/oDwZoQ69CrUZB/Fu88+it99cw6S8Efw1l9+iaUT3PmJdUBots9sBrewxVg+NxxuZO2Xc/gz/OujzTidTNaxY2mAtYek398N0LaU4fSn/4df/ysaGo8VeOXV+xHlY0ecb1qv2KFRTwse4ch8KPHUBwJM4VwZjLmLyChi5io887v/YMfJBOTk5SLp7Hb86WdTYJZzAN99vQlHE8rHjJJ196ixPVFFboNaUFddiqQraai2m4vf/Hc3LiUlI+7MHnzyxoMYp0vCV2+/jY1HU1HeOHolGe0xMkkOlZnRR5SR2rneFrbpGT+0djDfIfr2iwgRRZqWFtSTPFxsIyX5ODEcLBzhFayAMDEdqWn5qJ4TCAeSk7cSVjpyj6CFlrlNoPIEYivYEfHkJrdBg5wGzvt/wuoQa0ZtXXs/nRTZ++i3GemKWNvakGmtBXSNmTiw8VscjCuBc9RiTBBWIzP1IL75nyvcHF/EkmB5O67Y9aaYwBfWVhOo5hBVUaeuQ8Hl7Xjv9b/gu3Pl8F7wKt74/TOYH+4G2zbF6iF619gqRgDHCffgjf8uxCMXd+Gjdz/C/sNbsDsyHD6u8+Ar52KqHscDmaw3Fp3B1/85SAY1dbTBH8Qf7j+E12nfYj7yWhrq0NACfPnWfdj0HhnXjF+Kx154GvcvC4N8THNXekJUAHPZODz09pe4Q0MOpCWWsJSIISKLPr2zI556SU2udf6GHUnxOHM+A7Mi6DA9SqQMPSHS83XyvWhByuYyGSnty+EQshSv/vkPeGSOLznmJZJC5w3/kAnwtlLj+b9G48DRi1g40QsOPvJRb7lrghyqVuKl1XstI5zoJMZ6/hpBZUa/BLS8tKenKBOJ7UjhkPQJLJXWkDC3C+ZOiFowA86WjTi+9Ut8tzsG6eSzpaYiD7EHvsd3W07iCunIGBiry0IJ77CpmDXTE03557Dh0+9wlu5JbB3hQpwqV1dn2JrXIS+7GGpzS4hF5O0ZjUg69C027olFrWIq1jzxGt54/TncPtUJBTFb8em6bYgrJQ5Zz6N2RN8xssKphmaMezNqExHiTWVk4fgJfv3in7E5tgmT7nsTH773EhaP58TUQLpdXV9Mein/wi9e+QAncpqvj3szCylslW4Im3Mv1q4Ogty8ENnZOSivNd25MRBcBp2XxNEiW29MnOYPexs6vNWWobiwmLxVkwf6kjJSOWCevltQW12B0pJSlNCngnz0kcowTz0hQGuZhsZpcZUGQhEpVTMLcbpmbiGBfWA4xvs7w6a5HMV5Rahu6iQC6anMUXldQBFK7EhC4wG5tRz+M2/HHXP8IZcypX0zwksMqY0zIqdGwUGsR1l+ESoaW8gdxagEo0OjTIxDpUPe2W/wr398jPMZBaRcvpfi+pHCm4qs+RY7tOo9CRhXiXquXefpSbFc1UAWCC3kTFBpA2b5TmcQ+M5/GE+sTsI/tp/G//5wARvelRj9SqnJZUI9mRzX1gnhQnAZKK+D/1Tc8fgzqKj/BJsPfIxfnP8ONgpX+Ad6wkZXhtSETJQ3W2LN7z7CK/dEQV55HBu/3YfEKjvMfmgNVi6IQrAiBOZ1lSir+hJH93+DdZ5eePOF+XASmRhdS/i2EazELBy1SUvEVPKxr/CnNz/G6WIbLHr2Lbz27HIEu9pCzH3RDKDfiTBtrkF2/CHs2JqLusAFmPrsRDrYtBVB4npBPSpKG0iMQBZWIolxM2u7y/92g4DAHBJFMO59az2mPlmCerKOERhVHkjRoCkFm/7yIXamWWPBI4/i7iURcLOjw58bhaEZs1yVbjDscIk2DF0Otrz5Av6T7IsX3vkj7p7hDYW4dW3W1ZPzZwqT1KgXwsLIuerw8Jj7Yal0QUBYGMbJLiGP3KFczFkK95B2PhUNjchKSkQNWcnLnexhKxWPiegHJkZQASoKA5KeWYq6+ga0qMxIhluDugYV8aRkcPQNRNj0CjSP84ZSen21poVGBCtnH0yMCIcyyo/8BbU6ZpMoQ3D3y7+H1H0Lftx1GOcTc1EvIIu2kKmYHSBFc20LFEERcFdaQCixQ8DU1XjpLW9EHTuBmNh4JKWTfP1MKqrVIji5+GDK3EVYMIkmITn21BQ2oklvh6jF83H37bMwzkFG7GNLBM9ejYdraqHbHk/lN0DVRpmYzJRklCrTz2ilWIXku2t0ElXE4i+4gkObf8CZQgvMfPS3+N3zSxHAHP2R/p1GQycxoTktEjfGmcl04U2vKBFJMhI7BYbAQRODg5/+E595kMg70gd25HW+pigDp3d/hU9+TECTcgomTAiEq5zpIPLUMwLMaEYCpfs4KFz96YDDVB5ac+vqzHFKQTEmRQq4+YUjavpUuBBhYNQF7LnAMX6HwDOzhw+F0arefQBffxkEJ6u1mBEgh6osDce3fYatMekw85iL8ROIK2hqh+Ah7l1ziQMCJs7Hivmn8eGO3fjgj1Zoep45tvaAhKzirx75Gn/972GUwA8rZ0yAp/3YiCRhYgQVKbFOuh+//9tUlJIHYD3ICkvpCh9/UgIXyWA1/U684LMAeqkTXEm3pS2ZiazgGL4af/owCkK3IMhoIzSuPQIxyXUnY/WjHohaeDcKiiqhMpPCzpkFvRWSDpUWAiKk3O0IJlqtRFIm+psJR88QzFpeiepadmqppVOLCAq5Eg4U4NWFArxKiVWs856DZ/8YAIOVM9zcHMFEyzRjSUzoiSkrnoBbZBVUEhc4Ul7TS6RjZuTfkiInYTkqE3HhdCQyqSP9lIrqcoqP9lc8e+qja77OWIuJq0J6Fgq5Pewc3BExdxVWLZwIX0erUa8nMJj+FpIxh0/UKjx4+wW8v2UfPvh1HD63klBoD7KjVTWhtrIUzbJgrHzwISybEQilpYlxbQcDyhA9IyC/P+1nIRNGtTLp6To59GJiGE5M9QNsgTUmrnkUt5MS9bZj6/Ba3GbYUJBSPQs3VlkNc4dwrLznHiyZ5gXpWOf0mYmh9JmElY8+gZLqj/HD6a/xZvJ+yMknnzm562ioLkFRnS3mPvgk7pwzDo4yi350gOlnMTGCSgCpgz+i5vhdQ/7GqYxdECnc4E+fLonY42IbF4RFMQFep0QDQ+7kRR9PBE1gFn+0+DCl907ZWn/SJmouhpXC2fjxvpaH8Wo65zeTOSN4vPO1HO3+CISQKT0QSB/TTIQBuaZwDwpF8LgGBLhZE+etc+tNs2Udak06KjYuIVhw592IL9+GU1eykVErJuMGPaztlLCyJH2BhnrUUVzHtKspqLcOwuSoMHg7MrKZpy4I0DyzdZuAu156HTKvXTh88iIFOE9FVqMEbj6BiLxtMabPX4JFc6IQ4GJ9zedXl1L4hX4gYCZSwid0HCaI3ODnSYG721Nb/Xh+7GYxg9x3AZ577TeQE9EfHROL9AI9lK4k3Vi8AnMX3oYFsyfB107K5zjteEKJAr5RK/D0a8Ro2LcPx09dwOWkDLRY0j4csggr5i3HGgoeH+FBKhJjZAySc3F2lmlNTMHbnNwLsLRu3To89dRTrTf4vxyBdggY9GrU5MXjfIoWwVMnkvXj6JSPs3Y2Vhch9epVpOXVkLWnBXFT9KRwSYYNYorpRdp1Wq0azU2kJ+AdhvAgLzjatPdn1g40/tWIAMO0gfzX5OTkoaCwEJUtIrKgdYGrmzs83Mi4Q0aE6iikz29q9+ubUJSaiLxGGUWM8IKLvYz7SRtAB+hVtSjMy6YxmoviWgOsFY5w8/AgVzkOND4lfHx2wJI4+RoVHSwLkZubg9y8UqjFdqSv5wkvHy84KyzJXdHomNDr16/H008/bWw9c6XE3DR1Tpyg6owI/80R4AhwBDgCHAGOAEegHQL9Iai6kljtCuBfOQIcAY4AR4AjwBHgCHAE+kaAE1R9Y8RzcAQ4AhwBjgBHgCPAEegVAU5Q9QoPv8kR4AhwBDgCHAGOAEegbwQ4QdU3RjwHR4AjwBHgCHAEOAIcgV4R4ARVr/DwmxwBjgBHgCPAEeAIcAT6RoATVH1jxHNwBDgCHAGOAEeAI8AR6BUBTlD1Cg+/yRHgCHAEOAIcAY4AR6BvBDhB1TdGPAdHgCPAEeAIcAQ4AhyBXhEwsdAzvbZlzN2sqKggb745qKqqGnNtH44Gi8VisA9PHAFTQ8DW1nZA8fpYbL+bGd9PKBz4VsOCeDCP1O0Tu8Yiemg0GuNcvZltaF8PU/jOsOnOm3f7ujN8GZYikeh6XplMdj1iSvu8fX1vi7LSV7729wfTfxYWFtfr2r6s3r6z97AxyD6DeWdvZbe/N/BR3v5p/v2WInD06FH8v//3/xAbG3tL6zFaXm5vbw+lUjlamtOhHe0iTHW4zn+MDgTGjRtn3Cz625r+bLbdlTWYzYg9Y2lp2V1xvV7TarVQqVRd8rBrdXV1cHBw6HKPX7iBACNwGPHRU2JrQhuWbO1rI768vb0hlUp7eqzb66yPGVE20MTeOVBCTC6XD/gZ9g4bGxuwgwd73t3d3fh7MOO5tzZygqo3dEb4vezsbBQXF4/wWrZWbzAThz05HCeKtlNu54nc1NQE9hmpiS1YgznpD3bRYJyA7hJbhNk9xs1rW4RZPvaewbyrp/d09+5bcY1t7IMhSDtzV9rqrlarjV/ZZtcZL3aPcQwGmtLT0wf6yIjPz8ZWZ44xGytt+Ekkki5t6AnzLhnbXWB9OxjMBzvera2tO8ybdlXp8etg5gjDqbm5uccyx+INtoaGhobizTffxLJly3olOAeDDyeoBoPaCHmm/YRm1Df7jNTEFj/GSh5oYqeJwZx8entPfn6+caFxdHQ0nlZ6yzuS7nl5ecHPz2/AVRoMUcqIiJqamm7fdfjwYTQ0NGD69OlwcnK6nof172A4EUxkPZgN4/qLh/lLZmbmgOvHNvaeNrMrV64YywsKCkJnoqCQAkb3hPswN3PEFc/GE5uj7RMjEhISEoyXIiMjuxAmLS0tFLBc2/6RPr+zsVdZWdlnvs4Z2LwazNoUERExIO4aq199fX3n1/f5Oy8vDzmkEtJTYuUWFRUZb7u6unbBsqfnTPE6aytbsxhnMzU1dVB49qfdnKDqD0ojNA9bjNsmNKO2N23aNEJrOrKqNXv2bJw6dQq//e1v8eyzz46syplAbbZu3QrGEfnb3/6G5cuXm0CNR1YVFQqFkWhihGlYWNjIqtwIrw0jEtjBgh0m9+7dO6IPkSMcSqPurZ2dnbGaFy9ehIuLy0iv8qDrx8bN66+/jg0bNhi5zeywMxiuc18V4FZ+fSE0gu87OzuDLc48cQQ4AhwBjgBHgCPQPQKM0/nAAw8YbzJuVVpa2oC5zt2X3PEqJ6g64mFSv5iOQXsdFpOqPK8sR4AjwBHgCHAERhECnKAy4c5kOlNWVlYm3AJedY4AR4AjwBHgCNw8BJioj+nMcZHfzcPcJN7U2ULIJCrNK8kR4AhwBDgCHIFbiMBwEFOsOZxDdQs79ae+mlnAMRNcnjgCHAGOAEeAI8AR6BsBzqHqG6MxmYNZ+LVZ+Y1JAHijOQIcAY4AR4AjMAAEGEHF3EUMxmdZX6/hHKq+EBrB95lfjcbGxhFcQ141jsBwImAw6kEYhvMVvGyOAEdgVCHACCnmRoFZ+w114n6ohhrRm1geGxjDMSj62wS9qgJJMUdx5MQZXIjLgcHeDxGTZ2PB/BkI8baHzKJ3et2ga0Jl1lls+mob0q2X4JcvLoeHzHyUyqEpzENtIa6c2IoNW6ORXt4EvUYF9bVQZXqKsOEQsgCPPPczzAtzgbWIYWdAU8kVHNr1I/Ycv4KCykZoyGmh7tpCIBTbwmv8IjzwxMOYF2ADQX87zpTz6VtQU5yB89FHcSz6PK6k1MJp0hwsXrYSS2aPg5xwa4+DtrkUKRfPIPrkKZyNK4BW6oywqXMwb840jA90pTHaPrcpA9OPuhs0RuziYk7gxOnLyCzTwikoCjPnzMfcaYFQGMdcx3K0jUWIp/zR0WdwLqEEFg4+mDB9LubNnkxz3BGWY3kHMbSgLPMSDu08iCt1nrjz8fsxxVPaYfy1omlAfc4pbPzmB5yIy0N1Q4txHuuJU8KSyMYdkxbcgbV3LcF4t4GFfGktf2T+q9eU49y2z7EpuhIBi+7G6nnj4a4Q38BH34CcuOPYvfsk8szHYeXaOzErQH5T1v/uQhoNBYpjeToMBX5jtAwKWqoqxtH17+C9r04gu6QCNbWNMIjO4dTx/dh/eAkefPxnuH12CByJQOo+6dBUlYuTW9fhP1+eQINtPqYtX4S7Qy3JFUT3T5j0VUMTyrLO4cfPPsOmk7mob9FAr9NCf429QnsdpKlFUETMQjgRo9ZKFqS5GRnnfsR3G7/DkbgiNNIzjIhu48iYCSVwKKiGNGwOZvmHY7TTBnp1LS3Ah7Hxsy+wLToJJZU1qK1WQ5KSgLNH9uLwHc/j1edXIcBOAiHRSbqmPBz88kOs23wMCZnFqK5rgcFMjFMnj+LQoXm446FHcd+yiXC0HI0DrtNsofGXH38Emz7/GlsOX0ZRVS0a1QaIo6Nx9NBhxD7xGn75wGTIGXDXkq4+Czs+fhcfb49BRl45aupVMBNb4uTxgzh4eCnue+Qh2iRDoBSPAfzaQGn3V1WdgwsHfsC6T35EgSwE5jR3ozzHocuKZ2hA3L5P8fnGI0grqkGLiuY9HYra5rG52Ar5LWI4h0Qi1M0bo2NTNqAu9RDWrfsWhxIr4FpjDz9/TzgpnNEW8a+5NBnHdv6Az74+glrFBOhdwjHRLwpWZjfGYDu4f/JXFmqMxWplkRlYiLHhUEw3sb7ToyxxH37YEQd4z8TiBVHwd7bqRNGSm/7SNJw/cgCnMswx9c77sDiMAj/2pzsM9UiPIYLgVA4kfjNw24LJ8Fa0dX9/ChgbefSaZhSc+QYffPQjzmWUwNI1FGFTXGBWl4e0jHxcOvw9mnQSWMqexOoZPrAy7zpB9C3VyIs/hI0bTyKzsBLCxjTklatpoaEgqv3qLNPC2qBtQnVRJpKvFqGqSQcHdz+4yNud1ujcJrIJQKivA2Tia0uyrhb5KWnIzi1Dg8ASTp6eUFpLrsMjMBPB3nc8wrwUGKY1aOSATNyA0vQz2P7lOny14xyySxthLrGBvbMtWirzkFJaivIqLcZNmYJn53sQh0+DzOgN+OzbXYiOL4FQ6YHA8c4Qt5QhK7sA549vQz2F1BNby/HYbf5g5OvoTbS55cVi7w/fYMP2Y0guoPlGYV1kFLC4pSALV6tokxfYY/ykYNwZat3KQSC8kw+tw8cb9uNcWhVkbgEICyKv2jUFyKBwJmcObEKz3gKW1k/jzhke1zfJ0Ythx5YZtHXIjo/Gvt2HEE/jyczVFjl0uNESldRludNXIu1SMgrLKqAVO8LLQwmZRHidUyMQWsE/JBg+Xfayju80nV/Eja9Owe7vvkP01VyUlNfBvLAE1fUtxF2nVtD6rm0qwZVTB7D/yBmk5RVDrHdDUXE1WCjs4XIExAgq5hmeEVSDid3YH/xNi6Aigic1eiu+3xSNCpt8CGzsYb8kFMp2R3ODuhJZFw/g208+wYlKexQ5RGF2iB1k/dhxdA35OLtnO77begkWkxug8AmAl8Lx+sDvD6BjIY/BoENdUQZNhErIg1fgkacfwvwId4iacnFm9yZ8u4MmScwhnJwyGZNDPRGo7DTMaLGuLIjH/s2bcZIIMi0hbKZVobaukTg2zGpx9FFUTLzXUF2N8kYtrGxdMPv+X+GxmU7txpYAFjJHBIb4QH5NjmLQ1aOiqBYtjS1Qek3GsrX3YWWky/UTsMDMAjKFC/zGOV2/NlrHn6auAHHRB7HjQCwKW0TwmboQq1ctRISXBOXJZ3Dk6GmkNDlAwQhOI/2uIwI2CzklDbD2m4M1992DJdN8YdlSiHOHtmPrrmhkxp7BoQMzsXCaD/ytu/AVRg+UjDuVeBqnzlxCZq0Q3pNvx/JV8xBip0X6qd3YtPsCijPO4hhxQe8IHXdtTBJ++RlEuDbDMWIF7n/4Lswd70aHpixE7/oeW/efR+KZaByLmIbpE1zhJR3F+HUZCXrUFlzB8f37cDg2F7VaPWx1GjTVN0JFYjwxhcVpn/S0J5XkN0CrJhHrtKV47N5FGO9+Q0QvMLeEvZsXfLzpYNT+QRP8biCRfMnVQ9jw+Rf4Yc85FNc0QEdEpl7TqqpgoNW+piABx4kz9d3m3TiVVEiHbwNEBj10Wh2uaUAMS8sZQTXcRlyddrphaccQFiqEWGJOG0wdMvOiEXN+HmZH+UPhLLm2CJDOSUUWYmOiEZ2Qj0alwhiQ17zTAO+pQgZVHUqJki4rLYJZcTHKaijeD2XuOD16enrsXDcTiuEycTWe/4UDRGErsWbpRLjLJTA3TIAr8hBz7iryEotQUkDcmAaaIh0IKj31US4uHNyG7/YnorT52pHFoEVtPbFhRymMenUz6ijYcGmTGmYyEQVlVkJh5wS5gxs83exhSfpmnceZrqkWVTVNoEcgkshgQ884OHnA3tEFLo5y4zOjFK5OzaLNvSARsefPIaVECzufKbjr6V/ixbui4GIlQGPFbEyffRnZza6YFaqAhOnuCUTwmrIGjz/rB7hNwYJ5UxDgYg1zIlKdzMuRdiUBKeepPyhQdkWTgQiqTq8cTT+J01mYlomCvGoIFf6IvO0BPEeiUQ9BAaL16dh74DzqNU2oqm24Mf8EYvjOuhfPvjAetuG3Yckc0n+xI3G8JhxKVQ6uxCUjJ60CJYUkSm0CEVSjCbDe26Kpy8WlI7uxa98F5JRR4ynpifWiMhJUXZ/VN1ShpIaCNmuIoyezhdxWAUcS7TlT7DwHuQyidmLWrk+b0BU6aGsa0rHjH+9j/b54ZFfUQ8uoKUp6UlXQkX4D06uK3b0RX32+BdGpBbQ/tAayNpAIVEf6odfUykyo0R2raloElUAK30kzEeISjezCAiTExSMpexaCnIk7Yuy1Rlo44nHh/FWUaK3h5zsdC6Z60YlBD62qHsWZSYiLvYj4zFpIHbwQHBYCHwq06eEsh1TcCgXZDRkRYv/qjL1LBEAlLSDn6URWKsXkxYsQ4cpWD9IjUtcj+8Je7IxpxKRVazDNTwnx9clBBEJJNlKTEpGcmoWSegOkCjcEBAcjOCgA7vbSn8xVYGzL4TD9NALQyz9GUVPQEjz7q5kwl9lApC3FpUNnkJiegatnjyOztA5m1q5Q2JMuUKeTq7apHKnn9mHTxgO4Sgt8WyI0SUdINSxy7bZ33Mq/OlUz6ftUo66RTrKGUpzc9HdkH5JCamMHn/HzsWrVYkwJcoZMZH6dsNI11KCcFFibNaRvlhuHfV9WIX63DWwcvRE6aS6WLJ6FCX5OoDPG6E6kg1KclYKU5HzUm0vhaEdjS5eErR8fQpnGFr4BQQifMBt3BLjAkrBoJUyFcA5dgkc95pDeDxH76jIkRB/HlcQkJFw6hfgcIi5kDlC6OEIu6UzKjjI4iThSuBAXLoj0fKynYOH8KLhbNiP/4lkcORaHcpU5LKydEeDpcH3sgTR53CJvx7N+SyCUkqJ1Uz7OE3cwOS0FcWejkVZcD5GVE+yc7WEzuuWlHQaDQVOLjAsHsP3H/bhIenlMRMUS04lS08lH082JUFtTjmKa91oiKkrj9+PLyljsVMihdAvClDkLsWjOJPiTyFBk6sPQWH/iQalV0Ek9MHOJN7Q5sUjMKYOBiCm2nbL9VU/cPJ3QGh4h0xFmUY+ijDSU0T09y9MK57D+y8K1eZL6xHCEbTMtgoqmu8J3GmZHeiImowj5SXGIv5qN2eNd4SY1g5rEAkmxl3AxuQxipS/C5t6GySQSaK7Kwfl9P5D+wAkkpqUiu7gRIrkTPIiYcveejPuefAQLqEwZdaPAuKQwSpkpDLMR0Izi1NPYtv4j7C9xwd2KYISsDqDlRkcnkgwc+PhD/PNELWaZ+SHgqRlwsRZBYFCh6OoxbPluO46ejUN6XglqiBMjtrKDq1cQps5fibvXrsQUP/lPIqrYJL4VBJVxtAssYH0tMHNddgy++M+/iX2biaLSStQREWAfPhs+Ad5wsLqx2+tUNaR3cJhw+R5HEoohsvdGSIA9KpOuoFBNJzxiid+MCTWss7Xbwg1Qq5pQV1cNNZ3iWhprkZ58GcVCFWrqVLA9HYu4i3F44KmnsWZuAOyIg8VY/5qGWlQwgoqU0WtURVA3VCJXr0aLXoJTpy8g4Woy1j70AFZM94Gsi+JGtxUxyYsGDYk+iXNcTPOWDrGozLuEresvoLygFLU6KZzcPOEXMB5L7n8K9zMVABKZGkUnNEatbC2ozQaUpZ3Blq++xO7oBBRXVhPnTw3H4HD4BQeQ4YQxt0li069Km8sROHs1HlOGo07oiqBxlii4tB9fr/8MW6JT0SJxwdSFd2PFRKeOIidS4LcmPT/a6lAUdxQb1m/AidhUI361dXq4T3In3L1hR2vvWEjMKrkw6QS2fb8NBy7kQGPtjqAAWzYgkdtChIRKbRRvdcZCVVuJUiKo1HoNqUpkkn5RHrTNzVBLTuPsuYtITL4H99F+MD3UGaZN25sR8e2Dxc+8AvNZWviNd0Dsv/+P9lsK80KgsI9AaIfw29biSbvJaCaue3PGYXz/eSHK6lozDOf6bzQEoD2dEVLe3t6coGID1dzKC1PnToRHNCn55aTgSnwCsheRqMnHEtV5JBa4HI/MalI+Cw/B3HkRsFaV4PKBr/C3v3+FI5fz0SKyhbOTDKqKFJzLSkCMZQrkYdMQHuCKG1xrRlCRSwJGUJGIoCw3DclXMlBMRFR+eT0tL6zztaRYV4yUSzkooIU9MYlOz0xGTrwydWk8fvxiHT79/hRKIYe7TyAiyWpLXVuM7KRo/JBVjEaBNeyfWYEAxeBpWkZM3TKCimFgTAYwjpWUlFytyGu7jHxjNatU0DYUIistHTnF46D0IcJRW498IjI3f/EFth69ilo2sWbegUcWS/DD22koIIsjtZpM3UZpMhdZQm7vCA8fH3h5RmB8WACcJfXIy0gnjsklnNr1LaqaRVA6vIzFdEBgbhPMSOnayYmI8MBwhPiQ4r8/Lbi6GuSmXEVCchqObiPLqyYz2Lv8HPP9rikTj0L89JoWo35KA3Ewtc1NKCHuUkmeBcRMsZrEdyk0r9MSEpCa1wgr+z9h7RRyh0CcvvZJYC6CJXFarKytICULn6ZG4iY0VKAg9SpS88Mw1cemIzHR/mGT/24OW9cQzKSPrqUS6Rf249tP1+P7A3Go0CkRPvduPPPcWkS69sRqIh1HCzGkDD+KHWrZ2IxmwlBVU4yclBRklfhjgpuV8Shq8lD12AAtytNOYcs3X+H7g5dRqLJC6KzFWDJVjqw9G0n8ySyf6RDe5XnawC2VcHdRolTmDb/QcAR52EBD2KUnxuFq+nns+LoWGuIiypV3YQJJP0yXUUXjhDhPgXPuow8Boc1GnhUdDone1hqZE7SfkijeKXAGbqcPdFU4t/niDakOyzOMiRFUdXV1YCHbWIQRzqEygm0JH/I7M9H3KFJyU2hQXkFCWjEmutLAvnoZ8Qk5aJbawzN0JqYFkMJq6gFs+mwTjsQTR8RpHKbNWoDZk9zQQNaCP+6PQz5p/JcQV4WZpLPjQefBrFe3kDJxHWpIF0islMFJadPBrLVtDBhIoc5oCEsK11kx27Ht4HkUGRwxY9X9WLtmAcI9pGguTsKhbRvxw944RO/bhUmzJsNnlmuH8gYynrR0XGeD5NYmAax85uDZVywxKzMTSfHnEHMqBrHJ6Tj644/w9fOHt8tU0rsoxpWTB7GNFGBTS5pgbaegg28t6bJkoqSFzNl1AuRe3I2vP78Ea+dQzJwVCQ/Cuw9XVre26f1+uwCWck9MWng/fi6eBBnppNw2fRwUQvJjkx2LXZ//Fe9/dgwpMduw48RtmOBjT4SBBGKncKy690G4zxGSv6kZmBrqDktdNSlTHyLz98/w7a5YJJzeRc8sx3SfCRit1v8C0jJnn1YtMzNIbR3gETgeEyYEwVVC1lZpyUSUJiDz3E58/f0KzAheDn+79iJ1Aez85+K+J5SImJGERNrIzp8+jYuJuTi9dws8xkUg6MmpUIxiLh8bqoyYyri4n9xOfEr6i7GkFiFH6Izb8fRLT2E5GTswXl73SUDcvCV4/AUXTCeR39X4C4g5HYO41GQc3rkdXoFB8Fs7HjajGT86yCSf2I09e08jObcC5kpP6JrrUJxdiZwK0o+i9b8s4yQ2f6WBvRX5lZozG2FG4kgAqddM/OzpxzHNMA4zZpOYy9MG+oYixB3/Aev/uwH7z6fg9LHD5N+L/Pe5+JGKSve9YHpXBTBvY172RCsRcUP/t4oDe8ozRA1nzIf6+npjacOlnD549sgQNXIwxcjcxmPWJH8cv5yF9IxEJFxJQ5a3HPGxV5GSR9Z55M8ictYUuJqV4nzMPuy/mAs96UuMX/oM3n7jcUz2tELDVUdkX8pCJSli1pG3cRVZIUDStTYGOh0zb+RMd85C2EpQXR/vNBLaxgtjaBrHg64McSdikFtRDYFtMJwciXPQXIbcLAERDTASEnZWGiQVpeFCbBbuneECm1azpK4v7+MKI6jYIGGUNrNguGmJLDK09YW4RLpqTfJxiAwjkcuURQigz6o1a3Bp53/wp79+i5OZCdQniShYPImIBzVxBZrJ9w3jQpFri0qyqNz1Oc62VVqgQeqB/+HPh7UQO8/Cbz54H/fP9oVCcgPhtqym+NdMooBv1HLj50b9reASOBMPPv84zh6Ix5akYiQlZ5GYbwq8iaAyt3TBlBWPYcqNB+ibE4KnL8bqqjwkkWLwAfIBdjUuAzWG8bDschzo8KDJ/jCzkBF3TwElGT4Iqixg7zEZD/zi93hyVSQcRS0oSjqMf/76VXx4lHQdo8mlQvUCeCml0Nbm0NqQDZWVG/zJB45v5Bz4R87GsqZSXN73Of7x4WfYnZiDS6cuIf++yVDY3sQ5dJN7Q68mcXscuSkhYmrjvkso1doiZNoKPPHic7hrtjc6qToaa9dSlYHLl7PJYW8ggvxJVEiWlcFTF2DlmkKc2fIv/PU/m3AqPw2xF66iaEU4bGxGL34gNY6mBuLKXeNCaWn+XT5Cn7Z+JC59fsJ2/O2PeyCyDcBdv/8Y7z0YYtTtNbfyxuLHfoXFbXnZX6U3pi25G6XEIU3JJFcUJYVITS9Ew2LfLlaC7R8zte8CAVu/6UOch+7oJcbCYP+1JsrTXaYhajTzO6VWk4UPJaFweEif4Sl1iADoqRiByAXjZ0bBb/8lZBBRxbgiJ6xliLuajoJma4zzDMfMKC/oq2Nx9VI88htEsPKciPufeRDTvVtFI1I7R9hJLMjEmjb6ZvJYTaavrRpUrd3b1q96jZp0WFQga3eYC0WwsSI/SW2pbRzQb+NAoCL0GhIjZJFfFyqzuvkydn+ZgeM/SGBBpzcDydCb6mtQR9ZsYld6t56sItpe1FbmAP4y9iUj9mxsbMhqTD6AJ39aVj3p8VSnH8AHb3yMUqfl+M0bz2N+iJPRM7rQ0gEBQcFwsSNOXnIpGuuq0NhsgLmrK8Knz8FqEo1aJZFfpaYW0plSQ93ciOqySjBbGT3hQXatpLZWhXoSybRZiPy02o6Epw3QNJM+VHERyhqEZCLtDmfa8I0HevLoqdKQywRm5WdGBDIzHTYuPjT560qRX1iBFjNrOJLytMLakhxWkmiB5SHOpJDchTBFTh0RqdeMaUZCY4e+DqQD5BYQSOPKEbL8coiktrCzZ0q8JE4RSaF09YUfeahmqaWRiZz1xrFUlbgbn3ywDfnS6Xjk2cewcoYfbEmUamFJHGz/QPi428H8Mo1R0nGpI0s/kDrMqEzENS8jcdXWr77Apn2xKCPOFCOmHn3+Rdy7MBDWwu4OLXoUX96Mv7+9G/Ueq/DzXzyEeREkSqW8IitnctURCA+yNBVkNhMHvwYNpEMEm1GJXmujSEUhmKQb8zMqob2QhVo6HLaQ8rWKRNANNH5qqf2tStV0uBVQBAg6qNPUpC3FgGbSmcrMJSMIW2e4OtvByrjv0KGU5rHAnNZG2oWN85iMT4zPjCoYb5BL3Ter3SbafYYhu8oIqmbSXWPcKSa+ZqK/oU4mSVARaQPX0BmICtyLiykXkU4nrx+KBKgl3SRzUkb3nTADE3zFaE6uQGFeDbQSSygCycVChOIaLUwKhGQh1+optYU819LmToPb0M26wsw5mUkskwGz8xfrhNZuIGqaPF1ru8wApqthYeQYic2tSCfGCUqZBb2LBIJUhoIIOU8xcSsiF+H2BSGQD5I7xQYCc1DGiCqm1+Ds7DzUY6Pn8ggTFdMHy8oiDsAGfOHvBbPVUfC2I/2xetInO3YK6QVV0JPugIL0hmykxMkTKWlBWotX/SZjeVIacotKUVFRjqK0c9j+/SFkqy3gEbkMyyd5wMl3ClZO9YAtM9kaDYk2tPKs86RX9w0O54kRPHkaZkSFwtlGSAYT2Ti3+xscySbCSUSWVoHeJDIQ01hrQU7sTnz2fTTy1fYIi5qGyBBv4thpUJl9GYe2H8CFzHryQ+WFgAjyXdXN2B0N0BnbIJDA2X8yps+YRkrR25GZeQxf/FOGhqy5CPOxRWPOSew5X0EnYBERXgFwsRVBSPOqqbYIudnk5LewCCKyqhIbFiDY2ZL0+8qQeOoMEjLKiSstha29CxQ0RkdrMpCFY+zhXdh76BLSKgwkLvXHxOnT4WddjavnY2hRI309xuWmA6NM7gY/P0ejcnRzdT45QU1FypV6skhTkuP+KfBRWtDcL8LlY2eRll8FgcSZXH840Fwdvfi1jgsJvKfciZfcJ2JZKklEyBllZXUFcpPPI/rwCcSWCeHkMw0rl0fC3TkQc5eFtIruyAdY6hHihn6fCDPnEEyZPoX0ISlkDxqQd+U4tu6OJatoHZQRLvDxc4HVMGzyt3Jcsz2vd55B73eHq+6cQ9UJWZHdOEydHoy955IQnXgORYmUgRS9fSb7ImrGeNKtAIoYwaNiJwABbTxSWBiJHz1aKKbaRdr008jHj4qYIlo64WsZ4dRJHYmNbTMRKWMSV8qaFAyqVQ0oLK4grhJRty31pNCaguxGMvVnr6a8jLtpJnahDY5OcqczoHacjcdffwlr55BDQR0pwZK5KDtB1xO7SyR3gbeHQ1evup3a2dtPxp1qIf2j4ZIH9/Ru5ofKMXIp7pm1HQUHr2LPF++iIDYcvk5i1BWmkY5KNspJWdpl/EJMmhwBz2t+qMxEVnDwCjd+WNkGVRUyTlriIukl5NZKELri5/jTi5Gw6qRQ3FM9TOY6OburKkzB+aPHcTChEHv3kFM7nzD4uhBeBelkeUrm1xIlvCNX4vb54XC2JdGWvgYFKbE4e/Iweaouw66dW+FGpr6OMg3K88iqKJ9EygpPTIi8DXcuDO2X41qTwaubilo6+GP64lW4MyUD63dfweW9n+LqsR9g7ySHoS4fRdUG2DgEY/Fdc+DH5jpNRq+Jy7FgwmkKjRSL6C3/RWHicfi7kWVRaTaSU7LI6aAOzmHzMWPRZHhZj16KVNdC/raI01ld20RrlBAtZA19dufHiNulIy4wHfTomgWJQCwoBIpL6O14/U9PI4yMZXyn34nbwmNQcjIZe7/4AFkXQuDtYEFOLdORlJpL/rvMiMgIx7TZEXDrMcRUN51pqpfMJLBzDzJ+prE2GOqQfOxrVCVeolh+InhMXIvX/vwwvNo5mgY5o868dAanT51DbvlW7NwWAB9v2h/0FCkiK58sJlWwcg4mQmsBFkzyHGV6kGxPZZsqfeiA05VWZCI+ykNEV+v+2V2eoR8sjMhjoWeGI5koh4qgMFeQPJ98UvnE0EmTuB1kJSa0VsLLbzymR3gYlZlF5ETNnk6k+tg6FFEcq52HInCbrwCZZ7bhk39uQiyFPGFeWpnIhImXbtDSTP2VTm30r7lMAWdXF3jSApNXTbHnDh3CfJ8ZEBZfwDf/+AonyJO1kcZuGy1mCoybNBFuysvkSI+UX8/GY+I4V/KMaw1LTQ0Kr5ylk2IcGu1nkIfxuxBq17MqaF8dXkOOIpmSnT35exoOi4Ue3y8gj7PySDz0yuNIKFuHmMxSshw6gEuNekiY5RX5pvKOnIo7H30Qa+aHkv5UD6dX2vSEIhlZXJD1kI7CiChIC6iHrD3WxRRumFvDPXgmlt1L+mSGY0grq6VNKQEn0/Xk6E8GW/KSrPRbgOdfewnLyet0a2BkEsvMWYkVqSVQmyUgl+yKi9PjkKszh5jY1UqfEARMWoYnX3oGCwJHr4Xf9e6l0DtuYQtJ34xchQjWY9OxRAoy24j68jLoLZRwo/A741e9imdup/EmbQ3rIXaajHsevxe5VRoci89C7hVym3JWA6ElG6My4mRPwOK1T+CRZWHDFj/sev1v4RdzEnH6BAci0C+ewvdUEGZZiCtM71QjWvHIQsu+wBy3P/M4guVCSFxnkVjwXuTUfE/c0EKk0RyPJfG9SEoWvTTHAydPxxqKh3jXnACMEc8JnTAj8bGFpXEs2UhFxI23Rpf40mYOmLL6AazKbKR4nIUor6lA2uUC6MxbrSZdAkMxfdkDePJnqzDB/YadeacXmeZPclsis7EmH4/kFV5pS6JOEXHe2y3wZrSPkOsEmUwKmcoacoVVL4YRQwsBY0S0SqiGtlzTJaioYxR+kzAz0peiyKejsrCBWPfeCJw4BUFu5AuK/rOx9yFRSRhcjhegKH0H3nwhDt86grx4Z6OGRHxtDCmDttVBJvvdSlTR8xTWwyjes1DAI2g8JkaR76udKTjz7bt4JTEYsppknLmUTeFrW5OAWOatQ4WchtFGt3jiMXIZcAmHv/8vGsvNqCmQAABAAElEQVQzsXCqH0R1KTixdz+JLYrhHNWEiUuXUfgH22vPDbxj2YBgJwCmkG5hMXjCbOBvpicE5Phv+rP4+ych2Lf3II5En8GVLBXsfIMxedY8LFo4DxODPKDsTtv12gsFtBgp/adgzd2Loc9yw+rpXhDdTOX6QTV8MA8JIfeYiLte/itmLL+EowcP4cSZWCQVaOEeGoHJ0+dh8ZJ5CKVwFCI6ybUmMziGrMDLb0dhyR2ncfzoMZy6kILyFgk5xJtEnsHnY+6sKIxz7RzLcjD1M41nzCxs4BN1O375XgTmnzqCw8dOk6VZEbR2EVi4/HbctWo2PG3JB1UbhGSK7j/vcbzhHIY5hw7i8PGzuJrfCEtHf0yZNRcL5s/F1Al+UI4Sw4eeelEgcsW0NU/CgizT/PcexllyAVNU1bpyXdcjIX0HodgBE1c+QL77SGWBYUii1uClL+N914kUoucgjp68gOQiDYVBCsHUmYTfwtmYFOwJ2zEaHBlE5Nv7RGLu8lWoc9VhxtLxsLs++Np6wxwe0x7De+vm4SIF5T56LBpnL+dALXWm2JJTMGv+AjKwCoa7si3aR9tzo+CvmSOiVqzB4lI32M6chwhPO3QYKiRR8gibgYUry2BVYofbKND2T1GBGQhiw2YdT5vy9UQWY4zZYvysW7fu+vUR+0XfYkg58FfDg/MCDLYypSFiyTOGz04VGEip15j0mgZDceJuw1v3Tzd4ONgZbK0sDRYWEoONws7g6OJqcHakaza2hrA7/2zYHV9saKy8ZPjPM8sMIU4OhoiVLxk+O5lvLEvbWGg4u+Uvhrun+hjsFDYGqURkEMtsDXYOTgZnJ3uDgsqb+6tthqyq5tZ367WGwvNfG15eM83g72JnkNtIDWKRyGAhlhqsbRUGZ9+phnt/9YXhSoXmJ0H70ksvGftq/Pjxho0bN/6ksn7yw9RmUrI0UHiBEZ9mzZplxO3jjz8e8XUdiRUMCAgw4rdnz56RWL0e60ThL0bEGCUDEiN+CQkJPdZ1+G7oCQO1QdWiMpDfN5qvbMLqDXqd1qBRkdvZXubvSMAvNzfXiB0Rgoba2trhg2kMlFxZWWnEku35RUVFo7rFpIxu2Ldvn0EsFhtIf8qwePFiA0l3BtRmRhO10UeMVuoumTCHippGTsJ8Ji3G0gWJqLCoRNDSVZgX5nzdlYGA3Bw4By3CK3/3wqS9P2LnvmOISVEjctla3LV6PuxKd+LzLdnwXz4fYe4KWNqKMe22+bja4ADp+NmI8rc3co/MpK6YtPxpvOcZgh1btuPg6STU2Ebi7ntXI9I6C4fONmL2g7PgzJyYUbXIdAOukx/Am/8Ow8JDB3Dw0AmcTymBSqiEf/gkzF28HMsWkVKonWnDz5p6PVGbRyVz6XoD+RdTR4BxkUeJmcNP6ApSYzBnRjMdixCQ+EXYh+4ix68jZvyXaSEgkUjIfYo/UlNTjcZcw1F7E9/RBRDZjccDv1uHtaRcbia0MFr3dADKjMInEMt/xePs8/sOt4AwzLyz/SUxJt31a/q0v9b6XWhpB7/Jq/FL9jFaLtxQoFt4R9f8zBJR7h6JVT9jn992l4Ff4whwBDgCHAGOAEfgJiHAdI2ZuI8ZdBGHacjfauIEVSseZhRWoo/D1dACR5rTbWoaQ1swL40jwBHgCHAEOAIcAVNEYPTaCptib/A6cwQ4AhwBjgBHgCMw5Agw90J+fn5DXm77AjlB1R4NE/vuSt7HXVxcyOOu1ugB1sSqf0ury5yh3mz/Xbe0wUP8cltb22EL3zDEVR2RxTH8bqqrkxGJwuAqxSwTWWSI6xaKgyuGP3UNgbGEJRP3MVFfQUHBNR9ZQzsMRoXIb2ghMZ3SmC8NFpuILDTw1ltv4c033xyxlWebx02NN9gLEtXV1cbJ9Ic//AHvvPNOLzn7vjVYObwpbwZkHWQk4p944glOlPY9RLrk0FCUBpaWLVvWhShlRH77ecL8ZfUnrJSlJfPhdnMUEW7We7oARxdUKhUcHcnTOLX3oYce6oBVd/l7usbczLBy+kqd+6Ov/MNxn60xfZn5KxQKMKXr3hJbg9u712H7BzuUO5Cn+2+++abP53sru+0ee0df45WNabK2a3vkpvxlMW8zMigM3PHjRoKKLES5DtVNQd6EXsIce7KBwSZb29+RWv1buQj3hAmL6zQWElvA2m/S/WkzW5wDAwO7zerm5tbtdRYfi210NyOx9lhbW9+MVxktgvra0IaqIiUlJca53FZeQ0ODMRpC2++e/rLNcSCJjX22ZphaYv3AiCq2cbPQW4NNbD1iZfSVWL6e1i4WvuRmEQZ9HdzYfOipnu3b2D4PK5MdyEtLS0EuZPr1fPuyevre11rTG6Y9lTkU15kkh/U5+4SHhw94TexPHTiHqj8ojdA8LH6fj48PGMfgpywuN6N5fS0IN6MOY/UdLMxCfzaP9viwDTcxkcVz6n9qW6z6/8RPy9nXwv3TSr/xNDvd3qzEuFdtHKyBvHOgBB/bXNhmasqJEVa3MjHCYLhiwt3Kdo3Gd7O1iR34WH8xDlp5eTnnUI3Gjv4pbXrwwQcxd+5c4wl2sIsj2zjZ4jqQxBZvxj69GSk9PR3slD6UKS0tzRjLyZNi4ymVFPT1WmKEKeMQDHdiG2ZZWdmAX8O4EIPZRFh/DXTDZZUb6UT6gAHkD9wyBJjO2EAT43a2n5/seTaO2WbINkgWcqs9x2Wg5bflZ4S5k5NT289+/2V6mJ3r1++HR0BGtu7HxMQYxYCTJk3qIA4caPXYoYNJTAaa2L410AMEE1sO9IDIxg1zlVBYWGjcT55//vlh4S5yDtVAR8AIyu/u7g72+SmJTYTBnMBvlriATdKBTri+8GCEAltMbGxsOugNMIKFTbrhTgzvwRCJg+2r4W4PL58j0BcCgzEAYRsn4yq0T20bIyOkmCh7KAgqVj4ra6CJtelmifwGWrf+5GdSA6Z/y4gTRlAOlEhp/4428WH7a/35Ppg1bTCcaVY/to+wfYsRcRMnThwW/U9OUPWn10dxHjY4BzNAmSLjzUg36z03oy38HRwBjgBHYCQh0JOe5EiqoynVpW+tPFNqDa8rR4AjwBHgCHAEOAIcgVuAACeobgHo/JUcAY4AR4AjwBHgCIwuBDhBNbr6k7eGI8AR4AhwBDgCHIFbgAAnqG4B6PyVHAGOAEeAI8AR4AiMLgQ4QTW6+pO3hiPAEeAIcAQ4AhyBW4AAJ6huAej8lRwBjgBHgCPAEeAIjC4EOEE1uvqTt4YjwBHgCHAEOAIcgVuAwLD7odI2FiHhUjLqRM7wD/SFs9IS5v1tKDnjUlVn4mJ8KRyCIuDtYAWRsIcAoAZy2lWaj7zCagiU3gj0toOoh6z9fT3PxxHgCHAEOAIcAY4AR6A/CAwzh0qHssQ9+PjdP+D1P3+MPeezUKvW96dexjwGIpJKL3+Pt19/CxtPZqGmpZeYWrpapJ/ejnUffIhPt15GhcbQ7/fwjBwBjsBYRMBgjOdF5zaeOAIcAY7AT0ZgWDlUBk0l4o4ewIWkFCTWVsIldDIiw3ygcJeiP8wjg16H8qx4XEmKgyilGI0Lx8FgJez2WYOuHiXZqbh8No7CAcxBNRFurqJ+88J+MpCjrwDiDjZWoSS/AOUtEnj6+8GRsL+R6H5dOcVGKkApBa23spHCUmYDOzs7WEvFEHZDqut1FNqlpgJFxeWoaTTAWm5NoSWsoSCv67aS7vtKr2lCdUUphUiogFoggtTKGla2cijkNpCJux8LN+o43N90qCvOREZBI6xdvODuJIelRVvDDdCpmlBTWYzi0ho06USwtbWC1FoOe7v2+TrWUddSi7KSIhSVNcJMLIFUZg1bhRIKGxnE18vu+EzbL4Nei+aqXCRczYfQLRQhPnaQUEf0Z661lTFsfw06qJuqkJuRiUq4IjTEA1YWght1M2jRUF2K4sJi1KjNIbaUwYawkivksJGJYNalEQbotSrUVZbQ2ChBtUYKpa0l4auEgz3hS3O/8yNs/NVXV6K8rBxV1bWob2iEWmcOqdIN3r6ecHWwAVVpxCSDrglVJYUoKG2ExMEbPu7ydlx3aj/Njcpiul9UDp2lHFYU+85G4QA7uRQii67tZw0z6JpRXVqA/JJGiO294Ouh6FQm3af5Vlxcgso6HaS2Ctg7u8HJzrpbTEcKWHpVDY2tLFTr5XD3dIEdjYXrKwqNreb6apQWFaOyvgXmlrawtpLBVmkPpY0EbTO2c1tYmXmZVKbWFi6ernCQtysTNL/VTaitKqf4n7SeUbkCqQKOjo70oTVQfP3tnYu9db9pDrbUVyAvOxe1Zi4IDnaHVXuJD+FUX0XzqbAIdVoRJJZSWFsroFAQXmwOdqk5YaBR0bwlDEpLUF7VCIHMjtrvDDcXO+Na2O10ono011ehrLgIlQ0aCETWNNetaOwqqD+kMO/2oS4vH5EX2u+QQ15BVcUVnIxOQwUNNrOmQlyNPY/LyTMQ6hIAaW/jjY6MbXwsFl+I4cti/nR3kGQxelgyUC4ziu9kRk8ajMFgjZf7/Q8j3lisHx292JwiUrOo1F0X8X4XZ/IZDdoGFFw5gM/+8wWiK73x2B/+jMdnOrdOKjYhqrNxetf32LxzP05nGODu5QoXD39EzVmCRbMj4eNsA1G7GajXNKIsOx4n9u/Aj/vOIqVYB49xvnB1D8TUhauwcm4oHGQdh6NeU4+8hBPYvXMX9hyMQ53QGg7u3vAPmoTZ8+dj5kR/2NEzt2r+6VUlOLXxr/hgcwYC1ryEFx5ZgnBXii9Gva9trkL2ldPYv+tH7DudjJJmaxJ5exNhOgHzli7H3AmesG4PkPGZMiSd2ottO3bj4JkCWNCC7+Lhg6DIWVi4YDYmBjpD1umZGwNND01DMc5v+Ste/cs+WC9/D5+8ewcCFO03gRu5b/Y3vboO+XE78N4bH+OyxWL8Y/3/b+8rAKO8srafyMQ9E3d3IIGEhODuViiFQhVqW9+2W9mtbnfrSgUoxZ3iDsFJCBIgIe7u7jKZ/7kTIQRK++1HS/b739uGTEbu3Pd57z33yHPOfQ9D7bQ6hCc90ZW5sTi2Zyf27j+G5BodmFjYwsXNFyHDx2BUeD84muv3ELRiM6tDUdplHNq5FXuPRSK5zgp+bpawcu6PMVOnY3igC8z0eIhq5+RQNNcgL+UiTh2LwPHT5xGblIGC4ko0tmnDwjMM0x9YiEcenAR/G4PbbBx/Nlri+5RoKEnEkXXLsfpQDpzGPYN/vDwVDrrigtrR1lSJrGsnsH3zThyKuIRmS2/YW1vBzT8cEyePQZCXNTf13mtDicbSJERsXI6VezNgO+YZvPvqdDiKPpWcP5yzWXFnsG/vIRw/FYW4zAbIeQ8GDZ+C2TMnYrCfHYx0evd5L7Dp/Z3tqEw9gqXvfY9LjYF4+IUnMXukF0yEdqyigqTg4olD2LXrCK6ml0Fm60Hl1Am+wWMwbUo4PCz1b3PP2WdaBL7/4DtE1/njwWefwtwxPjBVadztKuMgK+48Ig4dwOFTl5CUXQGZpRdCwodh5LgJGBXiCztT7Xsmm3ojJP5WNFcg48J2fPLRaiQbTMGn373FNSjreCtxqsi5gsM7d2DfgQikNBhAzjXo7O6PISPHYkSYP+xuouuI+VLFNXUZEQcO4tjJc4hJKoCmtR+CBo/E7PlzMTrQiYZyr/kiDKfSdEQfP4A9uw/iclY1NEwd4ebsCr/gkRg/Lhw+dkboqefd7lr66nMa77J1DU4oJ++//77qz2nTpkGcQP2ftxZknliDpZvPo1qPgs4QqClrhqGtJ/z7ucG8l0dCWNfNdVUoLsxDdmY6MrJpqdKCLIo/ij0nMyEPnoHJofRuUUiqiQ2d7y0rykNWRgay8opRUV2MtMsXyLcqgIZTCCZMGghLWQtqacHm00PQqmjl9wvtOw/5pbVQ09ZXWVxob6bVWozs1OuIu3YNcQlpyOPrLe3qqsMTZbKeipUQ5I20iukxYT+5+cUqy6SVWpiGTAuaGjd7A1QWMT0yRQX59MqUoLyqFk2t1NjUqLDRguwS9v85xn/AJylY21obUZUfh2Pb12PtpsNIr2mCpvNQTA1xgCaFeUttPs6u/yf++vbPuJjfSKu3DhWlBUiLjcLJ88loNnKCm5udakNT7WdcrOWZUfhl+df4cvkexBbW8TP1KM7PRNLV8zh6KgV6XoMR6GqGbicMP1OaeABfv/9PrNh7CQU1jWiqr0ZhdjIun4/GtfQaGDr7wMuBVvufDSTnalNjLQriduPbj9fibOw1lOt7YkBQADxtDKFGZTTr8h4s/+IrrNwZhbzqZii4AeZlJOHqxXOISqiBQ/9geFrrdQtyZVs90k6txHt//wI7z2egtqUJddW0JlOvIfJcDDKrtWHv4QEH+e0tOKGw5Mftwafv/oAjKYWoaXLHpPvDYW9Eb6HqJvwBc+V3dKkU86m5DqXZsTi8/kd8u+kCistK4Db2YQx21qGSpERTZQK2f/kOPlx2APGcG02NdfSiZCP+UiQuxOag1dAZ3p7czDuVyfa2RpSkRmLDlx/io58jkFfHJcXNojA/C3GRB3H6egNsff3hTKVeeOigbEbR9YNY/umn+HFzBBL5He0atMD16DHUVUdTeTauX0lAlWE/DB3oCN17aiJTxlBWNdeVIu70Tqxbvw0HLxdCoWmBkDHD4GykThlUi7xre/Hpm+9g2cFENNDobKwqQUFWIs5HHEdiuT6cvNxhTyVUplobNFDZZ1NdGRX23Vi/biv2XyxEm7o5QsaOgIsx+6Q3JjN6Gz586338dCCOHn41HhzOfitzEHPyBBIrjeHmI+afwW29z79jKvwBbxHymF5vjvHYuq+wYlc0YjPrYe87CP39nGGqA44/FRGbvseX365HRFwRmtq4D5TmIi3+Cs6djEaRljtCgpxhdEPwsM9mVZ/HN36NFVy/VzPqYOsdiAH+bjAjJormcqRE7sSyL77Byh1RKKhX0AhXR2ttARJjzuHY6XjAJQxDfeQ3vGR/wNX/3i6V3C/FGixKj8H+9cvx49YYlFdWwn3sAoQ66VDp4xosj8OmT/6Ofy4/jJTSRjQ31NI7yjV48SwuxBUA5CV7udnCoGsNtlQj6+ohrPjkI3yz+RRyatoh09FGe30xEqP340RcO3xCB9EQ0u2cg2K0Su4dWTi+8Rt88tUGHGe/9TyouK48H6nXYxB9/jLyW2zQP8jjFv3g917rH/m+mJgY7N27V/UV77zzzm0P5r7ZJXAXR9PenIezx84gt04DwYuWIBRR2LGDG+GlC4hLD4XrQCtuzh1NSaWmujgdFyN2Y9sO3oyo68gqV4ejb3+46BWgrolCmR4klS+Kk6OuNBWRR/bQ4tiP45HXkd+gCQtHe5ip1aG4EXCjEFedSs73HVv/Jb47WEcrywc1CVG4cC0RhfDBsx9/i6fG2KE1/yL2bt2AjduOIj6/Gs0KJTR0LOEdMgEPLJqPaWOC4CCsfAp+lZWbeBY7N1EgnbiAxLwWWHv1x6DBwzB28mRaxc6QG2h3KEoU4hUZ0di3k1b3wVOIzaXbXu6CAcHhGDlmNEYMGaAi2d/Lze6W201s6yvykBJ/GScP7sLO3RG4XtkKI126ihua0CY8h1QWCmK24qNPdyBH0xMLX3kD94XYwUS3BckRa/HNin3Yv2U7PNwcYTPWG0a8wNbaTETt34JNu6JQZxmKxUuexMwQK0q7EsQeWoMvfjyGHz5bi6GD3kKIhbbKE6GoT8PuZd9h+/kimAXOw2OLJiPE0wKtJbE4sGENtp+OwNZN7vDzegKhttq3XMof9gTva2lGHC7GRGP/uh9xOJPKfAtg2tSMllaF8I+iuSgG+zZuwt6oPFiG3I9Fj8zDEBdd1Bcn4Ojmn7H68C9YumIQgj9/AI6dhkVTyVms+HQFTmUpEDT7ZTw6Mwzu1tooT4rAumUbcDpiJ7a7ucPdcQKcbwq98krbmZBRlIQDa9bgQFINdBhuqK7huGo6PK73TKpzXdeU5iHpyjmcPLoXmzaeQ60GBa+SQpTzCe1GHHwD4nb/oFK06k0G4/GnFmFMkAuMlcWI3rcWq7edx4Ft2+Dh7YYF4bYqhb6xPB2Ru9dws7sObffJePHNpzHEgWu0rRgRP/8bn2/djp/XB8Hbbi6CnE2g3piNiC3rsfdcFowCZuP5Jx7CxGBXGMsY4ihJxund6/D9sqM4s+sQ4h8IwzCrLsn0h82iX+1YyJj89ATEnDuMndv34PjlHCiU5tzk69DQQglIC7+m8Dp2/bgUmy5WwXX8s3jnhQmwM9CBovQi1n7xOXYcXYdtvt5wtBoLHytd2ozsMyMRV6OOYOe23Th6ORsKmKn6bGwWfbagpjgO25eyz6vNCJvzKl7/yywMdDVGbeo+fPrKP7Hz1CGcGTsUfq4WsNOnktoHWmtdERKuXMKl07uwYtU5FJRVo123Hs3NzWhtE1DVIolK6cYtRxDfYIuJix/DIzMCwatCTsx+/PTdJhxcsRRBYYF4ZriVapm0UiFIYp8X2efKVWeRW1KFdh32yfXN5c1OyetNPImtq9ZhX0wNvCY9h6eemIMQN0PU5cTg6O7t2HE4Adn5FdyzcMNAvFd4qfbWHCTEnMVxRge2cD3VcQ0aqNZgc8eo2utxdcc3+HrzZbRaj8Azzy3CcH97GCoKcXbnSqzecQF7OW88PF0wO9hatQZrC+IRsXUtNkTkwSr0Ibz06uMY048ynVGpte89jw/pOd516n4MdDKBnpFWx/com5B+djtWbzhKj7I1Jj62CPOmBsNKVouMS/uxbtUOnN72E7YEBeK1mW7o/NS9Qu4/+t4/SHIoUZNyGofP5qLJMARhYaMxxdoMKVdScJh8qPOXkzHU3wJW2sJ6pIJUFI8ja7/Ev5buQxaVI22ZDszNgLr8WFxsqKG1roM2zk7hQWutTce+H97Fx2tOIbuqlZ4eTejrqKGuMAsVjfVo0HSEqwgPst+m6kKkXI3E8eMpOHlaG4ZGBtDW1ICGERUuKl21uWex8t2/4+eTGWiU2aP/sJHwsGilK/0a4s9uxGcZKcgoegUvPjIKjgacKxlR2PzFu/hoWyr70FFZ/rkJZ5B57Rh27jyGv7z/AZZM9qc3TgvK2mRs++pf+Gb3ZRQ30dtFC6a27goOpl7CySOHMGbBC3j16RnwtRQWQt9o7dyQLuxcik+/3YIooQDqaMHWWo56MTxiT5USTTV5OLV9Cy4UyTD01ffx+uJRsDHoiK8HuBuiPC0NXx28iPPnr2NYkBv8LTVQylDLyVMXkQE3TFr4Al5+fCTkwiKkcuJOPl1pYiw+OMIFeHYxBkyzZ+wdKL26H1tPpKHVYhQefWYJFoz1hZlI21R6Q65BT1XBMkTGnsbpmEkYaOuOTsf1Hwwk501TMta8vgSfncqhF1MNJkZmaGqpoHIgCM4cXnsDUqK5OV9KgdJpOOY+8Twen+IFOkIoiz2IVTOy4v+NI0d/wankmVjUX59jbkHi4U3Yda0U5qEv4QUKtJG+VuC0htLfEZrV2cj/+hCunTuDq+OGwKm/aY850666J9eOrMOKHfEwYEjRU5mKKxXFqKxuo2HBQd0jj0tLdRYif/kGb3+0GWk0rLRkFuSZlaKYHiURlhettSoGO9afRAEt07lPvoDHHgiHq5kQpUq4W3DN5Rdh7flrOH02FmODbWCrWY/C9As4eiAS1YZeePr19/DUdNdO7pMSnhb1iLvwEvYdOYzoWcPhzvCBXnEKLsflo844EA/MW4i5EwfBgoqsWHdyC0MoqtIQfew0DvJ3QQl3zXumUCmpQB/Et//6BlsiklCvoQMdUznk9BZRnIlIHz2dFQydHsP2QxnQdpqN9z5+FZNdhcEnIOMaaclE7MurEHX6HK6PHgBXC3vUpRzB9//+GpuOJqBOnX0as89Wdsc+xfRQ0iNdmX0NZy+UQO6xEO//6zmEW8pUfVoEjcWosLU4mppFrlopahs5iD6hULUj98xSbv4/I7myBeq6RjCWG0LZpNYx5wlHS1k8jfpzuJqthcCpD+HFFx5CkJUW77sSPi6WQEU6nvsyEr/sOo/54dMpV5TIP/s9nn3+ZySU0TLXIX9RTqWffXK7EFMSivosRB85gIgLhbAc9ACee+0vmOJr0rEerWzhOXAiHnu1lhgZq9Y8P3VPWws9dMc3fIV/fr0TmfVcg1oWsLWsAG0tXhMviBfVWnkJW9ecRjEc8cjzf8WjcwbSsy0kqhJu8jZGBYqwjR6kM1EJGN7fCtayRpTmJZKrmQ4Nx4F47PVXsWCYlcrb3m4UgumTQ/D9/s1IycxHfXM/9iIwJ3Z13If3nkR8nhqCZjyIJ2g8hTsL+Qf4OnPD536dviwaR/aewYKJLnClN/C/rf0xI26vw5Vj+3GV7iKX8KEY6G0Ht4AwjBzoAXljCmKjL9K7w1AR0WpvJm/k3F6sXXcSFabheP7LnYi+noL0lDhE7v8Bi0e5Q0+rkVYalSRa4mnHVuH7zedQaRKKpz/agFMxCUhOuorjWz/HkkmBvNniFgiFib/EXWRTJ/fG3GEEXvx2Dy7GpyDt+iG8McUUV+jS3XQqneGm2fhg+Xps2bASP65Yjx37NuOzV2fAvjkOe+ki3Xg0FY2tlShMu4KoqCKYDngEPx2/juzsDLpEj2HVuw/CqekiVny0BpHp5WhkCLAm7SIiLmWjzXES3lh+GHGpabQSTmL9Z88gzKoKZ2lhrznC8JgYZx9p6poGsPMejMlzH8bL79DdvXwp/rZwGDqmPAfZ3oL68nhEnshDi/lgPDAnFHIqXV2TSMPAC6HDfGCtX4m01CRkFddQuFUjJ+U6UjMqYeE0AONGDYR5l3tdTRsGph4YRi+gsSIfp89cQzVDokpaMokXTiGd3jHfkaMQQgKzSVcNDDUS5L0GwN/LCYqKfMReTUNF258FIjl6FEgBIybioSdewcfLdmDLt88jyMGi2wmkbM5HckwSsou0yGcJw4hgl27BqiYzgpwYhIdZob0qDmcuZ6FNrAJe+8UTV1DVaonRk8bAz95MpUyJaaGmaQGfoBB4OBuitCAF19Lyb5oz7c3k0gjX+7I9yNX1xsNv/A3zfM2g2VJOL5BQqO7d5NLQMYWT3zDMmP8EXv/wW6zevAx/ne6iGlDHHWtHddIFnEypgK7XOG7cnrAx6bJL1WDg5MskFndYt5Ui8zq91mVtUJDYXpBEbws9eXLfKZg20rEHkVwNeo5hGDfMHlrVlxAbn4vKWgVJryRrM1FC1laBvLRkCvoiVNfTo9jSipametRUVZFeQG8CPdNGBp1C4x7BZmDhhpDRM/HIs2/iq59W4tt3H8dw3nuxuYn/mkjmTY29iNQmTQTOmIsRLiJs2jlYNRmcBo1AiKMZcU1AUnoRN04l9MxdETx6Bh5+5g2G3Fdi6QdPYqSL8A52TA5Bt2hrbES9pjbsBgTDQ95Fc6C3tToPmVmkTGiawNCYiRF9xqWuBlOngZg4exFeeOsLrN+5Fm/eN4gGS5ePoB1lWQm4npELBTm7IWPC4WvRsbGLjUHP2BJ+g8MRQEM58UQUUknAFzxcY8cgjJ+1EM+/+RnW/7IOf58bDDsqF8KYF//VZMch6mIS8rRcETJxEoa4atN7X4/a2jrUNzahhZ4xHSNT6IlQcx9oGrrmcO0/ErMefBpvffQdVq37Bs9OclKNTLUGqSlWM3JzIrUSRn5TMDbMFXLDLvNUjbSKfgj2d4V5cwEy4xORW8ELpNRqZaiupUWPCUX+8Hc169wD2un1rEJachYa2g2YJGIILY0usrQSdVnxuJBYgAazAAwKD4Wfg143QrrmdvAcEAh/IwWpFFFUuqjx/Re2rtl3V4euqL2Go/uuMQ4vxyg/FxhqNJM/pMXN2hlW8gtIjo9G5LUJGOzii7biDMREMRRYa4Lwp1/CywvDYdIpIVwHTccTD53EjnN5tKaoJLVk4NS+U8irt8LkJU/g4ftGw9O84+YbDx+PSYkxuHb1CJpUIT8hZZhFRH6BsdwR8/7xKV6fH9C9UTVnR2LXvgSUt/tgyUOPYGKIG8dJHhcjEZrGHvSkLEF1WRW+2ZaEEwfOYcqwKaoxKNh3G63EvKwM5FMZsLPxw9RnPoVPyBQk1Tkh2I2bIcff2Ca2SiUFVQ1K8nOQX2JDorY7xsx/GX6h05Fe2Ay5lxu0u4ThXb0D/2FnakbwHDpH9SN6aCq6gq0XOgSDkvgrmFVVV5iDFJo3cvfh6O+mR/J+j+9iFp6jRwAX5FFcLyokV62aiw4ozhYcN31YDAyAt4tBl56r+qCMXDZHH4Y/Dfcj/1oqSlrHQa5VgsykMi5ba/h5e8DapCdpVA3a5rZwtbeGvDmXvIBclNFqtjLsWrg9xnPXH/JmadhgwnP/xgRV30pUXrzewREQApdzo7W6FHkl1ajXtYOjpw8cLbqEk/iAOrPQ5HDz9IZm2yEkJ2dT8HhDv1GEWSsZAQtFPz9bbv43gQpTO1e42DJEnllNLEtQS2tBzDG0N6IoNQpbvl+Bw7TChz3xJp6e4o4DR7ghgsJdKKd3HYPf36GGriV8Rzyg+hGbd21RHArUOuaTCMmL1JOizERUUUa7BvnB1ZKcpx77kDqVSQcPG1hZNCKzlCTykgZu7DXkJBagUKGDgEFBcDfudd81rKiAusNoWxaycgtQ3dDIuRKM++ZPQfJHq7DnX8/g0AZvhIychHFDfWHUkITDO3bgWJ4GBi0cjQH2Pe/X77/Wu/NObvS2wfTU8Ud0qKzClb1XeS/F3KI8IWbNVCjzsugdlVlhcGgADHvxB7Us3BHgIcee1Dxmn5WhpkEJS9uBuG8xf1R9ViP2QHynAcAQNXUqdR0zOIU/iu/WDUKtdTCsObeEWGpvLcGpVUux9kwWZJ6LEBLoCiujXniLPu9Jo0LlOxv/+GR2x7crchnOEgRoYXgLo4y8zaJMFFfWw8zaGf7uDjfNLTUtPZjYu8PfUR8XcuKQnt+GwSaaMPWZScVjZmefeUy6IWdX9CnWNw364txEZJeUwNjGm57UBpxb9xG27z6OKzmtsGMW+/Ax4zF9yhj4CH5kH5DtGno2GDBuIX/EJSnoiYxGOq9IyIV2RnLEuszPIH+wTR0ewf3gQt5dzz1JnfPMyZuy1qQO5SWZKKTnTkluotvgOXjju2AUtlgj0EasmQ5KTGrE9/j3sgtoMhmJKaP8YcboRQcM9L4WZqC8vhFyVxdSQqxhJGRYV9NkhrgNo0vuMpy9noSMfPJs3fsWqb9rqHf63VNy3+l9/4PXlCiOOYGIlCqSwMvx0xtzsOqtTuDoZWpto8VonMy4dwzSmYlhXl3EFN18aBvZICiInJueIPNbNRmiE03BTaSlimRCbipKPYY1POyZxtpz+PQeaNJboq7RoXxxxqgx60+Ds1pDUwc2thY9Jgq15fwMXC8jobH0Ar74y1h88/zNhHJVpqCCmni7KXSyryOnfD6GBo3D3HmXkPLjNrw8exte1zGGnVcQhjCzY8SoMRgznB44cqjEiE39J+Dh+y+h8EfW4frrIXz3D2NYO3oxA2IYhtPrMnLoIHjZ3qxcqC60z/4jiK0M+VVVIr9aAXMXG5jQWu2xJDhyYfmZwdhQG0pabXVcPE1NStTyd72aLhelOYz1euyY4lp5v7Ro0VlpaeJSbinrlFFw6VajLK8aCg0HmJkZQrvLO9WJjbq2LsO3xjDQZrirgenvLMEAYcTf09ahuihI5iytbESLthkz1ZhqfjNAnIvaMDIzJ7lTyblXiTrKNJ2aCpQ2tjHlmOneJvSk9FoDGqK0hL4uNBvKUMmEiUYhBzUUqGJm3KG1P+Ln48VwGv0i/v7CWMg1s8VtYCN/SqXkiXH1GoR4+R43Do1NiaqyfNSwdEF/ltvQY1baTY3eSAPeZyN9bZJqmSghyhwwVb22llwZhvrNbMwYfep9bQzDmttAW4NZS1VUbOkyUKqZIWDai/jM3hFffShCX1dxYN11KlacvxyIntwZwTNfwod/nUQPd+/+bhrRPfxDKFWUn+RDVZYzxKUhQjfGt7mz9AxY0dBpz0JNZQ0am4UX6nZKkLgB7FN1RerQNrCA75BR/KtDDrbTI3Fk6Rv42+cHUGoQiuefWoiRAQzH91q+qo/3qX86rkiE3uuq6ikfKJP0WGaFZRRuurP05mkypGfO0KaCnswyodX/ahPYE0dlPcugVKK2upEG4jlGJi4w0zQNpSRsidB6QuJlnDq4Bas3zsP7n7+DuYFyotm3mzBqKku5BttlsLagM4AW8s04MYrAMjWidElxExOy6uhxADO49S3g7Msf/qVGfnFrA/mwB77BK6/9gEstDlj83puYMcCiRyYz94GqIlQ1t3JNm1DR6l06iaVSKOdMTKmIKlpImq/l3DS/eSx9G0rV6HpJsLswYlpVl0+cQF4Ds3WgA2MCp6vDuL2ePvT1udDbalBcWkSL/CzOX2eapAFdh8y8YDUK1X+9RyA8TKIJBUfRKt7bZXX3mqpiFvCnwwDuCvlROHR+XihkYql1TZY2ZnK0C6muRgFkbtSZ8deKNpLSFSQXKOhh4v/QlXsgIDQYzvSE6Rl4Yuxj/0K/qU8iIS4e8fHxSEqMw4kNH2Pn6m8QsvBjZt7MYlkIQyp3Zhj8wJtYNuxBZKTEM96cwPfH4frx1TixcxM2hs3By+/9DXOD5N1jEtfZp5rAp2Pn6xyW+JseOgHkbe+W0I9ktASJOz1aSmIpMBbCSLjThYJ7SxNKrxYzrqicidIYwhMpumcUQvXV4iO3fkwDmiRea8rEeCjMVOO5pec/6Ymbv5wMDtU1t6vu6m2ul9hoMiNUhxfVTuNCbHftIuFCdCPefpuPqGloQia4f6JvgRE31rrCOBxZTyLpxivQJDH75dcfQX85N4c6zluVZ0pwhASWN4/vTwLlV79GWPo9WztvtOq521y3eJ+6Bg0UCnklJ51qDfNmC++WaGI+3foxNchkIrGB84nva+ccFE1Rl43zR4/Q+s1EKUzoFfWGp4OMvMgEXClgokVGGjJKGtHfuu9wGlUDvwkucd1iPaleuc2183l1GUOX3BTVeO2cVyoZ1/H2G/+Kz6v66Nl55/oU67smBZs+eg3vrzyDGtMheObvb+Gh8X4M5ffabG/02McedVyXmPsCqw6502u/IHpq6lrQ0hb+P8p7zpWeaHRf0E1PUqFtYtiZ5XUKclmk2swRvhOewQePz8YgBy1yRaNZdmArNh3YjLdf4xzb8DYG00N9i87f3fm9edB1SV3ziJsdB0IJ3ek9vnlUanRq0FHB0J1YdwKnjibmi3ikQENFBk5v/Bxvf7wdSU3kYb37Fd5YEAiLbu9U50eEnBMoi8/dsnDpEOHeIaNsFG9p4z7w39juukLVUnoZRw9noElnCP6x6u+YM5SlDrj5qbOkgKgT1ZBzEj9+vhTbYxIRRaJpyAw5LOUWaGPGRlxCOurH2XS7scUNb2FsX7UpU5DKTK3gYElXRGY64/qFqKj1YoHHjktQcqNRcINqE4qT2MCVYsGIH94fbkBio77RyM+wdWK6sDaylP2w+P3XMW+kJ8y4uMQKVE24zt/q9CiIYpKaDak48ON3+PKXHIx++TO8spBlBEQcmcUbyzMj8MlLb2PP/t2IJBHWyZTWysY38M91uQiY/QwembMIo6ex3EAzSwWknMHmFSsYSovEgeMk2g4YBbO+tuK6gVIh0f2XOjd2XZJknej2TyPhsJIbt51u98t8IIqBVtOtyzifDoss0rOgo6tBXoo+s0rqmUFYipp63geTHhYzF1lLTRWLhypg6WhKr5OYK8awcjGGZgJLTVTUoElY2T1MYyULNNazBEU9rU8tFunT7+0G6jmkP/ixIHb2REldj2OnlaXTVIsqhjwbOHRmune39jZmuAnODiFyNDNW1WOTGTNBg2E+ZSkLD1Y0MZuIPfaYEwomW1TX83ktHRiaGVBhrUUWCfkHdp5GUmk5ZE378OasA3hNJRcVvAfk8ZGA+ukjYfhWpkv3/Hy8+PqTGBfowPTwWyRZ99j++Adibfb8FnV6U5xgqBmHEl5HfbMIk/eQtQzbNNVXqTICNWiUGenpsWgvCzKy2KR6KwuEFpSjllh1UQQ6eiZ/sbIETQp1WLBYoB49n2rKWsQeXot1O8+hynQwSf+LsWDyINgbkq+RcBwbf1qJrWfpSf7ODwGfPwxPgx7zs+dw78VjIYcozzoaNxxtI5jJtSjPqhgCraDKbHezF4T81arSeigYvjcwNIQOC5ze3ATCQoHv6rPHqyIrM/c8fnjnDXy19zq03KfjzTf/ijkjyYtkEk6PKdnjQ33noSrU170a6cU2MWCx4XZUsEBxRQ1DSOiRzEFDrK25lt6+VmZ128OEiUS3rgxiLxSt7klLecZsShnj0rpyd4ROexyvvrgQQ9xZQJcwK7y94ePvDTPlK/j8KLP9Ti9G0EzHPsQ7E/fq5jVIcxam1lyD6kksQFyGBnrblOgRauMabKitIj+sBTJDYqrHWhRdTWSys3bVnh8/w8dUvssMBuAvH3yA5+8LYhHojmztrreKVW3IArom2looqK7i3t3AuWvSw3fKfYAys6a6liVNLFSFjG+9Hzd666uPeoj6uzHEduScP4Dj2dWwCByF4aF+rF3hBAcHe9jZsvCjDXlE/YawSJgfHDXykBB9ljWOzOEbEAAHRQkiN7Pg3O4rKKqhu7Y8CzFHV+Pz5RGoYIq1yirVImFzlC/k2jk4sm0dfjkUjaxSbk6M7Z4/sB1b951GbIlwSXIRUF5QnWIIsOO6FJ2WatdV6jkNxayJLNSmiMO+rb/g5JV8tGpzM7Sz53htYabPsGBlBSt6t0Nbnx42UTeKqaaluSmsX8J6Gc0yui6ZQaTVjrqKEpJfueGJDY3uT7JgmdHEKtrFibh46QrSWZVYRg+dHoPTLVQ4qqqoJIiJSwXzLt+Arsu7e787N0BhvajT8jewc4EvU7ErMk7jWgZLKYhr7moUUrlpcShlzSgjCytYinCdzBw2rjawMBOZIXFIzhaC7UZrY7Xn/JRYpNS2wtrPFRasc6KuYQk3con01Vg3JykdxVUNN32mpbwQmXlFKFHTh7mtNcx7hxFvdP8nPupY/jITcg7s6epmxmRuGsmrJFLfaO2sn1aOjNQENKnrw4G1ugw5QTV0neAzgMTOuquI44kANSST32gkwhZmIq2ASoKBESwd5DDQ0IWpjSs8SNaXs6RFAxWI/DxWVye3qKCwmBWuObcUzXTlM5xewAzBvHzOY9bC6t4YbvT+Zz4S971rCOrC2KE4tXULgI2+GnKuJnAt10AVoeoclLKtDLmp+SgqVWOY1JbVuvUo1Fm12sEBDhpNyLp4BRm1vRQDRTmSr/Ls0BYZHDg3RLiwnZlZl07GIKPUDIPGzsfCeePQj9hbWjvCf8g0LHp8ISZ4qyMtcg/OxNfcNNf+THxu/a4OZUoYh8IyFN52XX0aNG6u0OIpFOejE1FPhb5na6vMQnwCN0Yl15wF50oPQ6TrfeIedNwHyrTOXUsU3hV11d57/jl8vjsZFoMX48NP3saCMf6woTLVKwrd1VUf+i2wEhdGiSqwYp0xC2b/2pgbd9Q04zxi9Z3uJjIbawpI+0itg6aJL2uWCa9e98vdD9grH1MmEXs1Zl2asQq4hYkJrBy8MWTceIR5WvLEBmZEasqgxRCinEVDBw5yZ1JIFRJZUqXtdoprd+9//gNxNd1rkE4OcW12Hv3ofWxn6YI45JBz1jNRqr2tBFnJBSir0ISJXMjxjlCdqJtXEH8cKz58G++viUKL8zi8/vlneIkZgtakfNw6X9Qht/OArZk+qrOzkMaECWEMdTeedFJZmIOMtCZoG9vD0caI8uG/r91FDxWVmNZshrNOoqjBCFNHh8ONJNNe9BcSIG3RbzAZ/hEXcSDjKs7GT8FTJHzPjU3Ct9sO4pMXo/CjKHNPr1IzC/yJ0v719DypJoG6IQKnP4z7YrKw8thRfPUayx5QYIr3tjTWorq6BtUK5lp3NbGw+CNab9e3mrY9Jj31CvJqP2VdINZaefkIfrCwgSPrWcm1m1CcQyJ5hQYCxi3Ai0yNDRNViPsFYqDNMezd/BamR3zJLAZNKkdVHd/dZIbxj87DUC8L8mO04TZwJPrZR+HA0aV47sIWmBuwhjsXcS0tpSalITzD5+G+cQEw6JJoXWPuU7+FOOmc9JQ2alQU9cx9ED7CCWuXxeCXXyIx0n007DvLJoi02KjTcSisJmHY1R1OPIpFnYLN0asfFetjuHItFhFURod7j4SlyhtIknt5Kk4fjUaF0gyTWBHbVCiurHTiHTIMbiaXkXDmBKLHhsDNxgfmqs80IjfxKq4lZqDNhMXm+rNa+j3MPOqw9ImRCh/+ktnAewDJ6EcvIz4umuUTxsB3sjeEzqdk5ffSbM75c7lMq3ZFGEm+qiCKpjUzuwbDYi/rsByKwJShbuTiWbHAJOdtaxkSL0cjOaucRzaFsxq4HZ11tJQ9R+Lx91wx7slS1FECCpe8uhpDEqzfte2997E6zRLPvPsPTPA1hbncAU7OJLt3ZVfeszkmNr2OL+8K/xp6hWC4lxl+ij3O+nPj0d9JDhczYSGTc5Ebj5jYVBb7k2OQBzc9ljPQIIHazssPAzy1sT35MPaduA9+M907+ZGsLp4bhSMncugh92ZCgwO5Zwwh0CvY3MA6QkrOXypkRrS0NTvXnSb7s3X0hLerOQ6mcfMoIEezpyfjnmHV+cXES2AmTC/h4dfm0ToeA0LgbxiJ2P3bcWJRGKZ4dFaRpzch6+IJRHKuaLuMIPHXkh6B3hcg7oH4EduVkI9iXrJ+X+IhfPbmB9gQXQnvaX/Dmy89gFAfOxjTYyze0/cbr0mlMAk5pTKlWYvSD/08HKgks8bhqXOIH+aOgaqQLg0bFoKOP38GV6ra4TQtFF5mvT154oo7+uzASoCgSc95AHxcHRAVkYuky+TWjvWBjxlxVL1dFKcuQnIik01YnsLZ1lwVehYv9Zkm7j2VcIGQag0SK2NvZuB7muJnrqdjkRPgZ8vje1S1o7gGWZD3Umw6ipRWGOFOuSYnTspGFCadwvqvP8NyRqOMB8zFS689gyms7WZ2h7CwvqMfBvnYIDLtOi4xES2eWb1DnAWPmBX8y0W9OiaVlahBHhoCX8eubN8+g9zvGshdVKjE9zEEQwKgy+ARmDLCgy53kSHRq5EMaOUdirGjr6EssgqGPC/Iwj0Ac55+FXqWrEV08DRL2KehVsYMr6BhmDbAGInnEqnMOMNEj7Wk9Adj0YtvwNhpB0NspxCTmo1mekFEWYZwB21OaAVMAzyZ9cXaT40Uzj7B6J/ZBk/73gRwklpdh+LRv5nAJ+w0IqMvIy45EznxkUikk0vXxB7uQUx7Hx4KZzNuezJjuARNwlOvtMB4xxFEXUpg2EuDR6G4IHBIIEKGjcfEUSHw5DEGmmKSuo7F4pfrYbn3ICLOXUN2cTPDZQ7wChmJkCHDMXLUUAR6Mr29Fzx96U8hyEW9LiFR1cjhoS+F5FUbhM6YgdBd/0bkps/wvb0mHp0RAiu1AkTuWIaNxxN4DMZQBA8OgIul2BjVSWAPRPjQgawbtR8ntyzHKnq4FozzgU51IonBK7D6RAEX9f2YNdKJNag6BJuZ3wRMH7kXibvPYvNqWwr2RRgfaImGzLPYtGEXziQxqyY8DMMHutyUvfNn4ycUdeEkUKNCo0aCvZq6HlwGDmMCwzkk7ovEzjWr6f5+FOP6m6Em9TS2rFqPY5nNcB41A2MCuqwwllgYcR8mB57Cxgub8NNP5tB8dAaC7NWQfX4nVm85pTpaZcSgMNWcEewoUSPHmlmyVk6d369aaKywXa2LSGGQaJjAvR9rwA22IjG0L2yKQjO4ET4RJwWIJjPyx9T7RuDg9T0k2K9UZWvOo6Fh2JSKIxs2YP/ZNGg7jEZ4+ADYCg1TTY+bWn+MHheCiK+OY/M3X1P4P4OZoY5oL45R/X0wvRrOY8Yj1NeG84azVsueSi4z1C6cxOWTu7DbwwwzhvvCkp6xhrJMRJ84ipOXC9i1H4nerHT/Z0+iX/s+1dwSmHH9kV/C6cXzHY1ZBX4Epo/Zgys79+Gzjzyg+/KDCHXRRnHcAYYtdyC5XA/hs8LohRNK+a1Xo1KoxMqkV0WDXKvGqnyc37cWOy+VMbnhBbz7xiIMZOkFHaGgM6yvTg6bSO65tadfG/i9eJ5MKCGweAqFhjixgoPVMvNE6PAwnLqYgvMntuAnendl80fAUbsUlw9swM8botCo74Wps4bSwLvd9XFt0YuiRl6ahpB/7FTPJoBlXoax/M5GFp5djs91mknpGA1vGx3U5sXi6NblVDJyYOg2G5PCbJhg0mHQ3wtEbv+dQpkWOAlulBgbOYcm/TDj/uHY/y6Pg1n5I6z0n8R9o32gV5uI/avX4XC0uJ5pGMLjZ6y5Blurc3H11CH8ciIL+l5T8dLrrMUVxHMBZcxyZikSkRgmKsf3ni8aBq4YOm4EjkavwSWGRNdZmUF7/ii46lXg8sHN2PgLQ/IMv86dNAJufSnsfnsgb/vsXdzPCaCmFcY/+294NVnC08sSer9iEWubuGLkA8/Ca1wLdC0c6ZY2gKHPMMx7mnHpyQ8iv7AcTdwQ7Ojat2ftkIp5ldCju9BSbBT0Rtj6Dsc8xrDDJ85HXmEFWmWGsLSxowKnQcIgs6V41I0DNWWZjjPC57wC++E8KNmza/O6gYOaBoWz60CMt3DFwJHTUFFRiUqW5G9oFVkvPBTUwpJhSiseodKxKPRMnDBwwiLYBYxhvJkHYjYyLmxCD4A5D8S0soBJj7ixuo45/IfPYiX1IZi6gNkNJNPI9Mh/MJfTFW8BM1P9P//IlBuX/rseCWVKlVrLxSeIwWKJaMhYqypwFl545hre+OIQNn76Io6uMmLUvZncjQJUwAmT75+FsYPdWTuqAzeZkSNCxs3Efel5WLnrDL5/OxG/fM1SCHQbV5I7U6Htz7o7jyNMVLvuXIWaXHxTHn4MCblfYs/FzfhnIosTkufQ1liN0tImGLuPwIw5UzDIsXe2yO+6tLv2pvZOQqe6II2LTYdY6VsHYsLs+3gk0k+slr4B7yUdxbc0LtqYkVheUQctKtuPPzEdbkY3lp+udSge+ctCZLy3Chd2fIGkU2t4FhtLV7AMQ2G1FrxHzMTMqUPhatwzrZ/fx+/sUE3EJQnFSZDdSYkn4VZTKHkqL+1du9z/ZUei9AaFOcepRbxU8SZ1A/hPfhSP8YiZb3fS4/xBLHZ9ZwANZmlVcI0pjHwxZfosjA926PRCMexl5obBk+djQWIeljHU/68XIvETD65VMgOuKC8bSlaTf3DRRPg78OBfFTjmCJo0B1NT8rH+2DF8+48L2Eh+jXhNIUI/FeLwanOE3j8Po3xvlzn3v7zs//jjgoAvNnURcmJWmvCq0SA1svbB5Ece4/FLn7D0yzd48eo2GJNH2MJwckFuDeyGPor7pgyGu+WNo426h8DNVHgo2pkmryYy3TgFFQwP19PTLviK9Rc24M0l+3vU9uIn6ZkWmanmciu4DxiDyZOGoR89er2jD93fcU8eUFZxbilpogqFSgUVU/E9h0yl3MlC8bojLAj9FqK3M2tbnUeSVZSjsp6K54In8cBw1i277Zg5X5lRq1R29klxpq5tjoBRM/GgyNBdw3P8fv4QF/Z+z7Af954mHplUUcGjtwbh8ZeX0MDXVY3jtl3fkyeFMkVSvVASKc1l4uaLxshP/+lLsPhqDpbuPUEO3VVs+ZJeTwVLJRSVQikfgNnTp2HUAGbPcgq2MguvsbYGVbzWsobD+PK1q1jRi5upZ2zF/dMctu6hiVakjAAACHRJREFUmHn/NAQ6M4uXfE7XsBmsX5iFsjXHsH/52zi/y5Qe91bejzKGAI0wYOoCzJ/o2ZMy2zHG/5J/7+5ZflyghqzMa29DkGiB9tZQuzGhFaFryFOprSxhSiVEbNSC4a9Ld7aNvTPcvbx5dpcbHFnqwJgp9dZ2tjAXcVmxStiExSBOlbe255lxHl7w9nAjX8KSig0rAFMJkrNukVC+RZ96Rjxg1kaE4To29+4xdD3ghiPT1uNJ13JY2drD2dUDHh7ucHHiCes8tV5fp0eWBt+rSVKsidwaDk7ksLi7wtFexJXJpWLKd+fwOnsWygdJfDz93dbRBa7kPTg7ij5JvNYTh8L+KjpdI7v3v3nMTFl+DnLLgICx01m9m2dTqTAwIi/Kg6RqGRqqCpnFmMU6Jrqw9QrF9PmPYuHsUfC3N2Hqeuc1ivtN4rUdr59HgaG6JBdZWXms2mwGd3Lt7n/sSR61EgxbFuXrRoWfMTB3gIujFcNlzRxHFnKKahgqs8OAEVMxf9ECerBEVfrbeEH/ROQU9YWIu5oBA+9wjB7SH05mFKIMcxpZ2JGLZwF9DXLH8nORU1AJNSqWgcOnk7PzGGYO9YBxjzmpxjCema0LwwTc0HlOVn5GOgrJXNez8sXwyTy+ZuEsCjQeqCzCnr/aKDAVdMcnnEeGehBmzh0ON56l1UdqDKqUl/IcnplZYIVpC+fCz0qsLVrI5AU5ujrCQo8nHtD1n5ldQm6QIVxYkHDmgw9h3vShPPeQSlbXdBLrmgLbycWeCS8tqCjMQlJyERT6PCA5bAoWPfEEZo2g944KeMeaVGexRSa0uDgwYYBHsTTwzNA8hvSLKtGmY0HvdjimzF2Eh+ePgw9LmXR9z6/C/Ke90I4GnnOWnce5Y8OCu5OCYEVOlMh8NLR0gLurFbQZRi7MTEZaYSOJ0i4YPJ7HNC1+AKOC6NHX7bGeuscsOHfsM7cc7ZbBmDp1ENedjGR/nrVako/0VGZBVrNsSQGLgjZz8yVJsoXp8rWCp5edibI2Odz9fODB9d1rD+3+hnvzoA3l6ddYNV3ONTYCg8jBNKBBr8UkEWt7B9iQ+9PKMF9OTg6K62Ww8QzGRBYwXvzwFPjb8Z7fdtAKJhyR31lphn5Dh7PAJY9j4b4mojDWlOnO5ErqqzUSqzzk5DFBwIB0lvApWLh4CeaLItN3CH/d9uv+hCcVzXUoyU5CSoU9pi2YyWKnwkDjGjSQw5l8Z7kuw3yUzxk5xWhU4/mNQWMwZ+HDmDs5jHXiOkLLwlsqdLHmygLkkg+VX1pBcn8x500LvfUk+4tzSFkKpiiPyWPFMngNGgQPOxPVuZqaLDVk4+gAa8pJRW0J70c+yurVYekejPGzeUD5wqkIcjLtMzKr5y35PWf5sQyL8P91NEH81qBVK9ry5cuxZMmSjhekf/+/REAQVct4gHFaTjVMPQbQra1/Q+Eh8V+ECtJTmG6eVUxCvwm9hA5USJ1gRYVW6za8JsEhq2bdoYy0dCpHlVSO6AG0o9Lk4ghLHuLbrUz1QLu9hQKAylR6WgaTFdrIIeHxJU7OcLSzpjJ+b5UpMcy2Bp4ndjUZTUbOcHOxgzmFaEdjUVdmrZQWiLFno4jKkY6ZFewdnODsZAuTzjP8Ot/c/auNtaZyszJI2sxh1Xh6I+S2cHRygr01a1fRCr5zE96HRmau8SSCSgseMupJwn5vRf/OPfyRrypa6lFKhepaGhX0ocGsai1Mqc5G/k91cS4TeNOQWUjFmaEtYTA50bCxpDf31unEEE9rE4msmUjl3MguqGc9KWsaL85wdRZnS97mupnFVl1WTJJ+LvIKiln0kwknPIbF2toO9vY0drjp9h1lSuDScbZmVkYBajRs4R9AhbobCF5/i1Cm0nj9VL7rWJTSwppzRRh5Yq7cTpnq6LOBG2EmvcXV6tYIIJXCkGe7tTQwWSI+FteSCtAmUtcZupEZsI4aD7zVVBdYk4fW1AItczf4kVLhyNBo10zvvIP3+Jc4gD0OCXmgsecKB2th0HUOiXOrropJIunc4PNKUKc0UBnPTs5cV+T5dkN6yxWwz6zrSMxth6WLK5zoKOjuk/emmRmoQjHPyspFSWUztMX65vxz5pw1FeHpPtd4H6lQFbOCfHyuBvzDgpgQ0sNAI05VPBA5g7W1sorqoK5HZwbXoJBXcmOWPOperGK+iFMHEhGfRGO6hd55hoeVjF6IJBDhSRVFUJuZod+qZcvza1m42YpV07u+ikpXvbgfNBoz8phA0a4NOfcOJ2dH2FmKw+77HHCqAa1YsQJP0FgTTZT4EYkKvZukUPVGRPpbQkBCQEJAQkBCQEJAQqAHAr9HobpVxerRgfRQQkBCQEJAQkBCQEJAQkBC4LcRkBSq38ZIeoeEgISAhICEgISAhICEwB0RkBSqO8IjvSghICEgISAhICEgISAh8NsISArVb2MkvUNCQEJAQkBCQEJAQkBC4I4ISArVHeGRXpQQkBCQEJAQkBCQEJAQ+G0EJIXqtzGS3iEhICEgISAhICEgISAhcEcEJIXqjvBIL0oISAhICEgISAhICEgI/DYCkkL12xhJ75AQkBCQEJAQkBCQEJAQuCMCv1rsNioqCp6ennf8sPSihICEgISAhICEgISAhMD/dQSETvRb7aZK6a2trdDS4rEDUpMQkBCQEJAQkBCQEJAQkBC4BYGWlhbIZD0Pqu94ixTyuwUq6QkJAQkBCQEJAQkBCQEJgf8ZAjeF/DR5hPSOHTtUPdjY2MDY2Ph/1pv0bgkBCQEJAQkBCQEJAQmB/2MIVFdXo7CwUHVVQle6Xbsp5He7N0jPSQhICEgISAhICEgISAhICNwZASnkd2d8pFclBCQEJAQkBCQEJAQkBH4Tgf8Hi0ChSanNZowAAAAASUVORK5CYII="
- }
- },
- "cell_type": "markdown",
- "id": "2624e4bf",
- "metadata": {},
- "source": [
- "When an array has only one dimension, its elements can be stored one after the other in a contiguous block of memory. \n",
- "\n",
- ""
- ]
- },
- {
- "attachments": {
- "colrow.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAADWCAYAAADFNak/AAABPmlDQ1BJQ0MgUHJvZmlsZQAAKJFjYGDiSSwoyGFhYGDIzSspCnJ3UoiIjFJgf8bAxMDPwAnEMonJxQWOAQE+QCUMMBoVfLvGwAiiL+uCzLp9qneX98mX6xNmXItjMGSOxVSPArhSUouTgfQfII5PLigqYWBgjAGylctLCkDsBiBbpAjoKCB7CoidDmGvALGTIOw9YDUhQc5A9gUgWyA5IzEFyH4AZOskIYmnI7Gh9oIAq5G5kyEBd5IMSlIrSkC0c35BZVFmekaJgiMwdFIVPPOS9XQUjAyMjBgYQGENUf1ZDByGjGKnEGJFqxgYrOsZGJi+IcSinzEwrLnBwCC4HyGm4cbAIA4Mj33lBYlFiXAHMH5jKU4zNoKweYqA3vzx//9nWQYG9l0MDH+L/v//Pff//79LGBiYbzIwHCgEAGmsXtKRMhyuAAAAYmVYSWZNTQAqAAAACAACARIAAwAAAAEAAQAAh2kABAAAAAEAAAAmAAAAAAADkoYABwAAABIAAABQoAIABAAAAAEAAAF2oAMABAAAAAEAAADWAAAAAEFTQ0lJAAAAU2NyZWVuc2hvdIDld/wAAAI9aVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA2LjAuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIgogICAgICAgICAgICB4bWxuczp0aWZmPSJodHRwOi8vbnMuYWRvYmUuY29tL3RpZmYvMS4wLyI+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj4yMTQ8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICAgICA8ZXhpZjpVc2VyQ29tbWVudD5TY3JlZW5zaG90PC9leGlmOlVzZXJDb21tZW50PgogICAgICAgICA8ZXhpZjpQaXhlbFhEaW1lbnNpb24+Mzc0PC9leGlmOlBpeGVsWERpbWVuc2lvbj4KICAgICAgICAgPHRpZmY6T3JpZW50YXRpb24+MTwvdGlmZjpPcmllbnRhdGlvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+Cmm3plIAAEAASURBVHgB7F0HQFRX1v6YAYbeexNQwYJir9h7j9GYmGI2PTGbmN2UTXbzp2xJ32x6MYmJplhi7yV2RUWxV0BAOkivwwwz7z/n4eCIoAjjULxHH/PmzXu3fPe+75577r3nWkgkECIQEAgIBAQCbQYBRZvJiciIQEAgIBAQCMgICGIXFUEgIBAQCLQxBCyN81NUVITTp0/Ll/z8/KBUKo1/FucCAYGAQEAg0MwI6HQ6ZGRkyKmIiIiAs7Pz9SliG7tBXn31Vba3i0NgIOqAqAOiDrSCOsCcXZcIU8z1bZ24IhAQCAgEWjUC15hievToUZOZL7/8EsHBwTXfxYlAQCAgEBAIND8CycnJePbZZ+WEGHO2ccquIXZXV9ea38aPH4/Q0NCa7+JEICAQEAgIBJofgcTExJpEGHN2zUU6EaYYYzTEuUBAICAQaAMICGJvA4UosiAQEAgIBIwREMRujIY4FwgIBAQCbQABQextoBBFFgQCAgGBgDECgtiN0RDnAgGBgECgDSAgiL0NFKLIgkBAICAQMEZAELsxGuJcICAQEAi0AQSumcfeBvIjsiAQaAACEnTaSpSXFCAvvwAFBXQUaWDj4gEvT094envASWUJC4sGBFXrFr1OjZLcTCSnl8ItJAwBrio0IphaoYqvAoFbQ0AQ+63hJe5u7QhIOlSW5uHShRM4uHcvDp08iwvnLyA+tQyuwV3Rs3dfRI0aj9GDu8Hf1QaWilujZW1JJk5uXYCPfo1H1F8+wIvjggSxt/Y60wrTL4i9FRaaSHIjEZD0UBen4+Tu1fjhm4VYF30JkqMDbK2toLKzRGnGSWxLiMaGtdtx5pU3MHfmAAR72MOywdwuoaqiGGnxJ3HkZBzsEi5DImIXIhAwNwKC2M2NuIivmRAg0lXn4NSu3/H5x99hS5wOHYc9gIceuQdDu7eHj5s1SjPPI3rdj/jfN2vx47tvwcruv5h3dw/4Olo3XOumRqDahKOHXi/JrlKbKcMi2jsYAUHsd3Dh31FZlyqRfnIHfl+0GDuTVRj+p1fw5l9moIuXTQ1pu7kMQlB4d4QHOOGZNxZj45rdmDSkAzwc3WBNYEn6Kmgq1SgrLUeVHrBUqWBtrYLK2hqWloor4VjAgs03FJ9OTzfJooe2ohTlWkvYOdjK5p2aTgCFWVGhhl5BvQYVhWNB91ZWopIiUFiSnV+vhUajA32DtcoGNiorKC0kukeNSg39ViVBaWUFGxsbWFsqaxoVrZp+r7KApbUl3V8dppbClCyUFA6n2+paMxPtkKmrqoRaXQmNVkfORixhRfdYU9iWlI5btEhdybf4aC4EBLE3F/IiXrMioCtJxpFd27AzthjBg57AvD/PJFKvPbBJdKtwRM/73sIPfiOQad8dkb5OsOKUkm0+P2kvViz8ET8t3o64yxq4BEdg8OjpmDVrCob0bAcnKyJ1CwUUCoWsqVfpmNj10Gkysendp/Dhyb5444PnMaS9K2zkPWwklKfuwRcfLUSy22Dc++AsDPTMxpbffsXGo5fh1iEUqvTD2H7wPHL1/hh21/3400OT0cUuCztX/IZVW3Zg99EiBA8cjweeeBxTB3aAuz01Broc7FnwIRYfs0XvscPRyT4FO9euxdZDydDYt8fIaTNw992TMKC98xVnURI0Fbk4t3sZfvx5FbbtPwudR2f0HjAMYydNxZjBneDtZEMNhFmLTETWBAQEsTcBPPFoa0FAQmFaHE6cSUS+UyimTxiNXr61Sd0oLwondBk6CZ3JpqKQ7SoSihM34+PX/olft59AaoEGvAV8/qk9uHT2OPbt3I2HX3wd82ZFUiPAGnv1LGLaAIEIXgdJk4KYrWdwMs0KKXmV0IZIROzVLFmWFY8jR2Nw2skZvUaNQy/LdJyIPYjlv+xGESXJgsYFuIGQcA6Xko9j1461iFSdxZZdCSilnXSqdBIurYzDqRMZ0H3zH9wzKBhOVdk4dygW+zacx7q130CvK0NRcRV03NBYnEFC3BnCIg/vffQMentY0rhALuK2foYnnvkcx3NL5fuktGxcPLUPK5f8hilPvonX5k5EtwDnWxhvMMJTnJodATGP3eyQiwjNj4AeJfmpyMrNgcrZHZ1C/aG6Sc1ncq4mddK5tWnY9vN32HAoCz6D/4xv1x7E2fjzOLZnOd59djicCw9j9c/fY8PxPDJ1kNLPzxLxS0S8EtnZq8oKkVekRpXSDc6OZBoxsmuwhs+ir2LiZRNItUlH0lrALbAn7n/tB+yMicGulR9iZidLxB/YhE0x+QgZPw9fLd2CA4d24JOnB0GVtxubdhxHVn4FNToS2ffJxq+jeEutENDjPrz1zWpExx7Btl//g+ndLHHx2Eas35dMzY4eFUXpiNmxGRfUHpjzwWacSU5B4rlYbP7lX7i7kw57f34XP649gksFWvMXnYixUQgIjb1RsImHWhcCZJPWaOjQEamyLZvMFQ3OgISKS4exZe9FlHsPInPJvZgyMhKetpbQtwuEl6MC5UWF+Pngcfyx9yyGz/aUzTEcPNvYZZJVV6Cc4oalE+xs2VRzNXKlFc+Xt5CJWL6ffrSyVsK+XRf0nv4s/jp3Ojq5q1DmKWHYoHVYf/YUQie+hE/efhjd/ZygspTgmz8M3608i8T4ZGST/T/UiXoanENVEEZMexTPPjMLQ7v6wcnGEmqPSiQeO4gDy5Nw5lQiCqcEw5Ls+BXl1JOg3kG1bd4a/kFd4BMQjJDQCIw9UYCQfp3gaS/2QL5aci37zKiKteyEitQJBBqPgAIOLt5wd3GmOewFuJSeB7Jg3ED0KEq/gLjUfKi1VShIS8Cl3Eq4t++KiLBAuNtZkzavgKWVLTxDOiGyCw2wVhQh+WQCLldKNZo+R8AmGyb3KjbLsP29espMTdxM6vwPpNnzzazBWxK5q2wd4ObrD1+abmllSYOjdo5w83AnIreGe6eeiAx2h4OtNaysVHDz8oGbrZKmchajrFIHHYXB0SisvRDauRsiOgXB1YHm5NMgqI2jK7y9PeGi1yA/LRdlkgJ2zkEYOPEuRPmrseHzZzFj3BAMHzMDc1/7Hzad1aBDvyGICPWCg7Wgi5qCa+EnQmNv4QUkkmcKBBRw9Q1FR9KwrY4m4/j+WFwaFYr2jnVpoGQVLzqG+S//BavLx+ON9x5FMM0+qWKTCnMvJcdY21cQ6VoRYfJMFTZhXzvBkQdTaWaKnT2cVTRjpSwPRaVaMrlQKIbJ8RxgjTAbK6hXQYdM9/x89Y9yOEoaxuULSstrZrRY0EwXTpREGjengO9VkLlHbiRopowlxXUlGFhQGDzTxZoaEW0F5YviV1o7I7jPTPz9wy44e/YCLl68SI1fFs7uWoo9G5fAves0vPDy05jYNwTO1oaQahItTlogAqIJboGFIpJkegRU7u3RY0BPdPUqxdm9q7F6VzzK6lLbiRxzTv2BtWRWySrTypq5s4cvPMgMkZ9wDvFJWSjUMIGykDZ/6QJOnY1DltIegaQZexDx6Yk0WRRK0pxp2qClfTt07u4Ki5JjOH42G+WVV56XNMhKS0JBWSkkule2zTMp02HBGj6bcuSQrvxhTqXrekq38XVJp4VaQ4ROhK/kZ68cFED1vUY3Szqaskm9EA1RvbUtTZ3Ul+NywnZ88Y838X20JUY9+CSef/l1vPX2v/HuO6/j/kGeyDm2AVv2nEJ6vto4NeK8BSMgNPYWXDgiaaZDwMLaDeH9RmH86NNIXBKD3z77ECh5AGMHdEaQF5k17CygLclF8vmDWPLlclwod8TIYX0R7O4AV68eGBDhg2PbYrBu6WI4KcswMMwN2twL2L1mKVbuvgRb/+EYFtUZTopCItMqeRDVUqmUSVqhCkDUxEHw37EGW35fiYEdnDC4gwNKkvZj6bJduJieD3jSvdwQsM7PpM5ZZ4I2QEDnTPyyyLZ7/r36K2vq3KPg++Vn2ORDP9aEZUTsqNJAXUE2f9LyvZ3toOI57upCpJ45jp1nfXDPg6MwIcwHAboKeDlV4ayzNXRkZiouqYD2SoNSk6bq6MXfFoiAIPYWWCgiSbcDASWc/Lph1N0PIq9QjSV/7MA375/DRl83ONnb0uIe0rS1FSjKy0ACuQIIHTYH90/qAT9nG6iUHTGO5n0fif8J+w6swGcXo7HExRaSOh8ZZK/XO3bGlOkzMbqbF5R0TVdFA6UWvGiJTT1EyKTNh42cjbsHxeKnQ4vxzt9i4ONkBQ3NRkmKv4ScYjW8aYGTgqZAsqZePYhK50T0BmEtXEkaOZO1jmbQVOvy1RSroIVLzjQxvogWF2lpcZGe45RNMczodBgRu16rQVk5ETvZ1m2d7ClvtOjJowP5yPHDqhWb8d68LKwM9IBFaSE5RstFSkIS7EIHY3CfMGoIeDKnkNaAgCD21lBKIo0mQUBh5YiArsNw71N2cG+3EdujTyExOQHxGTlE9oBrgB8CgkIQNWMmptxDrgY6e8HOisnVER0Gz8BjT0hwXrcNB45dwLk0Hezcg9Cx72QMHTMek8bTqlUXa2jz7eDq0w4dAkrQ3t+lmghJg7b37485f34Kpd+vwp7DR3FY74LADl0weHwYkk9dgFWAL2nIdlCqnODjH4QOoaUI8HGBzZWcKywpXN9ghFH6Qvx4YdFVirV0C0TXEF/ofdxgzzN+FA7wDg1CcJgWft4usKWFUwaxsLKBi6cf2odW0eENWyU1QJ4dMfKBh3G2aCUOnz2GrccqoLRxgodfO4T0n45hNLA6OSqMFj/JS7UMQYnPFoyAIPYWXDgiaaZHgIkzqOtQ3BsQjgHDE5CQmITU1AxkFwDuwe3Qrl17dOrSGaFEntZG882tnUMRNW0OfMN7YdjJc0gv0sHBKxSdu3ZF545BcHeo1mYtHLzRdehMPO8QhYDePldWdlI+aEVrp+GzMc8tDIMOH0eO5I52YTRjpZ0VkojY1c7tEUmuDCwpnP7jZ8EpUgsvstnbXEmD0s4FIX0m47m/dIZr71BK21VsrN27Y9aTf0aUU0+E+TjCinoIPSY/iKe6SfDr1AEuRjcrHfzQY8RM/DmwCD49gmRXCQobF3QYOAsvuobjxKkzOH8xD5ZuvnIj1yEsHB1DfOBIUyWNorwauThrkQhQz4/6fldk69atGDdunPyNR8ZDQ0MNP4lPgUAbRoDt2qTVVv9vw/lsWNZkSjC27zfsMXGXmRBITExE+/bt5di2bNmCsWPHXhez0Nivg0RcuPMQIHv2VWvFnZf9Wjlme76Q1o2A6F217vITqRcICAQEAtchIIj9OkjEBYGAQEAg0LoREMTeustPpF4gIBAQCFyHgCD26yARFwQCAgGBQOtGQBB76y4/kXqBgEBAIHAdAoLYr4NEXBAICAQEAq0bATHdsXWXn0h9G0BAQ77iq8hNAB+8QQZPN1TRvqR8iKmHbaCAmyELQmNvBtBFlAIBAwK8GOiHH37AjBkz0LkzrSp1dUVISAheeeUVlJWVGW4TnwKBW0JAaOy3BJe4WSBgOgQWL16MTz/9FOfPn0d5ebmssXPohYWFmD9/PpKTk/HJJ5+IFeD1QM69m507d8reMI1v6d27t9xAGl+7084Fsd9pJW6G/JaUlCA2NvaGMfXq1QtOTk43vKet/rhw4ULwcfbsWRQUFJBHRu015MRafGVlJbZv344//elP+L//+z+MGTOmrcJxXb7UajVSUlLkOhQfHy9jdOHCBZSWloK/Gwubr2qLktwlG0xYgYGB8vJ7f39/dOnSBVFRUQgLC6v9SJv7Loi9zRXp7c8Q+xE6cOAA0tPTkZWVJb+ETFCXLl2SIzcQ041SUtt+zC+ep6cnPDw84OfnBxsbG/l7x44dZe0rIiLiRsG16N8YjzNnzoD9evz444/Izc0FN34V5Bedf6tPWIvnBvLFF1+UCf6vf/1rfbe22uunT5+WyTotLU1u6I4dO4acnBy598INHhM3b/LN4xCsoTNmtyJcL+Pi4sjlsZK2EaSdo6yt4ebmhq7kvG3o0KEYMGAAIiMjbyXIVnGvIPZWUUzNm0gmpZiYGBw9ehQnTpyQXzwmHcOLx5988LXGCjcQ/OLxvpx8sMbFn/wi8kvJRM8Ha1t83fAy9u3bFy4uLuAGgBuLliKscZ86dUo2FTBZHTlyRNY4L1++XGNyYQ2SiaVDhw6wtbWtSTpjsXv3bpw8eVLGlInpf//7nxzW3LlzMWHChJp7W9PJoUOHZBxY+87IyJAVAjY7MWlz/WHMWCvnT1MJh1U7PIMywhjzmEbPnj0xZcoU3EOumtuKCGJvKyXZxHywNsQvW2Zmpkzg/JmdnS3bf/Pz82UNk1+6YtowufaL0sSo5ccb0igwoSckJMikv2PHDvk5BwcHuUFg0nd3d4eXl5fcGAQHB8svLXfFvb294ePjAz6/HcLkxKYDJgwmYzYXMHmxZs54MW6sObJwGkaNop2cxo8nF8Ht5PQ6OjrKjZchbWyKmDVrFo4fP44VK1bIJM+9Iw4rKSkJy5cvx5w5czBs2DDDIy3qk+sHp5cbJMaBMWGzE/dS+OD88T08OGxsSuGeGpcV99y4HLmh5x4cX7uZsPLBjQMLj00w3tyIFhUVXfco38e/88F1nNPKPdCvv/4aTz75JO67777rnmltFwSxt7YSM2F6mXC4q8+2XNYquaLzS8cvg+HlY9IyvDCGqH19fWWC4peOCZO/Ozs7y0RluOdmn0zQTOYcF7+ATFpMhNyIcJx5eXnXBcEkwGlk4ftqi52dnazV8xZyrAEzMfCnQdvnc04nm31Y7O3ta9yf8nfuGXTv3p1PrxNOL5OSQbjh43RzmtmMwCYCJisDkXO+DLhx7yM8PBzTpk3DkCFD5N4FNzw36mEwyXEvhLVJLp9FixbJPYBz587JDQiXFw8Sjhw5EtOnT5fzaEibuT/ZdMI9OSZwJnLGg8uQ65dBGTAuT3Y5y/nicmEc2CzC5cINHJcRH9xgG8qRy/VmwuGzcsLCdYTLg+NmF7epqalyL5M/2YzIZWcQQ53iZ9iUyL/xoPZzzz0nm2q4x9gaRRB7ayy1JqaZKzx3i3/77TeZLLgy88vJXeK6hLurnTp1kl9AJqigINq0mUidiZFfSD74JeX7GipMiEx8/AIatDj+ZC2OCZ8/mRxZQ+V7OX1MGPwi8rW6hJ+7mebPaeaDhXsAxgO4TMBsf61LmLANRM2/czyGxo/TWZcwcfPYwKRJk8AmIzYfcaNSs3dpXQ8ZXWOiYwJkzZ7NNRs2bJBJh0mMGzYmItY0uRxZy+3Xr58cB8fJz5paGHcuAy4LJkwmcU4LY8Hp4YOxMMaKG1fe14HTxnWH6xErA6yF82/cy+LvXH+aIqzh1yXcwBgaGU6fwQzDaeceBeeJCZ+Fy5dnKPE17r1yg8mmLzb1tTYRxN7aSqyJ6eWKvWbNGlkDZO3PoAHXDpYJzkAqTBSsVTHBMDGxNtVU4YbhZsKEwV1lJgt+OZlQeCCNu8784nGjwARjIBS+fjNi5waDD4NwOKYWbuD69Okjz8DgTyZ1Jt7GCpfFxIkT5XnuPMd96dKlsnZsIFM2Q3ADxSTPBMekyfdxeXFauMyYQFn4O/cGjIV7GtwjMQg3pNwbYSwZUz640WUS57Lg61xvDLgbnuNPTgc3Qhw/a+Z8cHychoCAAPloaMNmHG5jz5mUaxMzKzaGfPEnN5CHDx+WMWUzDuPBYyKMA5uQXn75ZXlGDTdErUUEsbeWkjJBOvllXb16Nb788kvwbITawhorv/jDhw9H//79ZXLil5E19KZqVLXjash37oIzQdQW7nIz4fMLyC8lkwxrifyScq+DGy8mH84vv8QGLZLP+WU1tTBxMHmx5skHT+VkQueG0bhH0JR42STAGi+bCFgD5t3OuIHmvPPMGs4/H6xxsnDDyQ0CY8hlamiM+XvtXglrqoynQZjEGSvG0oAtXzOYOgz38SeHxXnnsQM2q/DB51xnuGHh+tPShLFgLPlgYQWBTUncQPJYycGDB2vOuTfLGDzyyCMYPXr0dY1ES8ubIT2C2A1ItPFP1nT37t0rL3ypi9TZrsmDcYMHD5a1w27dusld5ZYIC2t8bNdnYSKpLayFs1bOGr6xpskEz1om/8akz8Kkxg1BbWFi44PJjEnS2NbKmhsTNpMkfzKBGUiMNVM2N9wuYRMLD6xyw8sEv3//fnmcxNjGzHFzA3Y7GjHueXDjZSBzQ945Layd82+tTbju8+wkPvg92bdvnzyBgLV4HsDmRVCMJZve2KzGDWVLF0HsLb2ETJQ+Hmz75Zdf5EFS4yDZDsxaMWvpDz30EAYNGmT8c6s8Z9Jh4cHHuoQ1W4MJhl9W1vpri8HMwcReu8fCJM9kzyTLGmt99t3aYZrqOzdsXGavv/46oqOj5fnx3FthbZMHBw09lqbGxyTNeeQeCZMZf+eGlAmcseWjISa1pqbDnM/zADorOHzw7KY9e/bIDSdP9eUBbG7IeAC8pYsg9pZeQiZKH1dQnrdrLPzC8qDW3XffLU+fY83lThDWso1NJD169Gi12eaGmA+DOYHt7GwX5t4KX+OxCf5k0xQftYUbCW6oDLNQDGMB/Mm2cv5kcwoTGq8huB2DsrXT1FK+GxqvBx54QDZ9bdu2TR5wbynpu1E6BLHfCJ028hvbSg0zKThL/DLzCztixAjZZtsWtPQ2UlSNzoaxOYEDYa2dy5x7I/zJRG8wPxlHwnWByZrJm2cJ8aIpFh4wZ+1VCOTxpalTp4KP1iKC2FtLSTUhnTzIyFoZmw1Yg2P7NGvpL730kmxmaELQ4tEWigCbTfjg2UxC7jwEBLHfAWXOGhlr5zw1kKe18QDp22+/LS8EuQOyL7IoELjjEBDEfocUOTs84kOIQEAg0PYREBtttP0yFjkUCAgE7jAEBLHfYQUusisQEAi0fQQEsbf9MhY5FAgIBO4wBASx32EFLrIrEBAItH0EBLG3/TIWORQICATuMAQEsd9hBS6yKxAQCLR9BASxt/0yFjkUCAgE7jAEBLHfYQUusisQEAi0fQQEsbf9MhY5FAgIBO4wBASx32EFLrIrEBAItH0EhEuBtl/GzZpDvU6N9NiVWLA8Dh2mPIyp/YLgqGopXgP10FYUIvXcURw4GIPjZ9Og8OmMyF6DMDwqAt6OKigtmhW+hkcuVSE/5QyO0uYQR0+cRUqREp7tOqH3gIHoHREKb2cbtCYtTq/JR9yRndiy8wx0gcNx78wh8LdrLYXR8GK7XXcKYr9dyIpwAUkHTXE8Ni34BgtWJ6GDOhy9OnshTGWPZqd2IsKyvEQc3LgUPy3dipMXU5F1uRgW9h7w8V+LvXc9i+cfGYOOnvawbOl8oi9F3N6VWPjLKuw/HoeUzMsoUlvAztkDm7f0wbgZ92P23UMR5mmLlp6V6temCnlJR7Bp6QLMXxsP994a9Bw2EP7tWs+eo839+gtib+4SaIvxS3pUacqQmxaPI9sW4seNp5CWUwicTkZ+hRY6ynNzE7umJAundi3DF18sxtE8W0T0H4sRvk6wqMzB8V1bsHrBt+jYrTO8h3eAm11zp/ZGlURC3vnN+O6Lb7D6cC5cQjph8MQRcCfttjQnAcePxWDNb5Zw8vCG59RIuFm1fGrXFiXjyI5N2LDtKBJS1YBPIjLyKwFB7DeqCNf8Joj9GjjEl6YjoEN5Ie36vnEJlm6JxdkTh3G2UALrilXkF16rl2jzZYqlWfmlCsXZ5xG9dTNi0oAB9z+LFx8fj66BLlCUp2GTSzae/+IIdh+5iGn928GViL1Zk3ujQtHl4dCKX7E2OhVeA2bj4TnTMbJPGDwdLFCScRRLP/svFm49ggP7YzFySFe4ebVsrVfSFuNi7HZs2LQPFy5r4exsTfWmFHmFpZDg0HLL4UZl1Ay/CWJvBtDbdpR6aErzcPFYNA6cyIaDZzdM6irh+OZdKKKMM6c3u0iVKMlPR1LiZVh69cTU2dMxsJNrNWnYBqJDsBdUFjoUFZdBW8X9ixYsUjEyU/NgE9gfMx95CNNHdIGnfXUPw9GmI9oHe8LOIh7F+XkoqWgR6NcPJpnH8pJjsHnNBkQnVsI3oi+cNalILK5AQXG5XHdabANbf66a5RdB7M0Ce1uOVAlblyD0nTQH8yItEUj7ZoZaxeDZ/YdwkjaGbhnUooCNow86RPTH4Koo9AwhEwwXCRFLcfpR/LHzLMosvYkUfWCvsmzZWqLSHT0mzMLjg7pgfP8QuMhmIwmakmzEkea7KyYO+RZuCA8MhLtjyzYpVRQkYN/6lVi/NxGKwGG4e2oEKmKX4WK0FqVqMsUIaTACgtgbDJW4sWEIKKBy9Ea3EbPQjR/Q00t5IVZ+VK+7YoZpWEC37y4LW3i1H4T7/xqCMVpXdHBVQq+rRFH6SWz66TMs+iMVnhEPYNKgjnCzt7596TBFyBbO6D39z+htFJakLcCpHb9j4U8/Y83BFDhFTMegIX0Q7NJyib2qIgend67EsjXRyFC0x7S7ZmDyAB22nLSCpK+ERqtrIUqBEdAt+FQQewsunDaXNDKus8beErR2pcoRnkF0UGp02jLkJB7D5t++xMff70CZ3xA8M+9xDO/kAbtWMNhYu57o1Rk4tms79sdeRG65PQJd3OHqYAVdlR6wbnmTHvWaIiQf3YRff16DY5k26HvPPZg1ZQD8y6NpPKa6zuivfNbOq/heNwKC2OvGRVw1IQIthcyvz5JEA3PFSD9/gGbBfIUvlxyC1ncInnr9bTw+IRyuLd0Mc32G5CsKWz/0nTAd6RUWsI0+gaTD6/DLr17w8n4YQ9o7N/uMpNrJLks/hGU/LqQB4CTYhI9GiJ8tcs8dQErGccRn5EOj1iHz/GHs2lkABzcfhISG0BqDlj0IXDuP5v4uiN3ciN+J8ZG2pZfHIFvQ0BdNydSq85F0cid+/eIL/LAhHnadJuG1d97Eg1GBsLVUtGzbuqEeSWrkZ2TTmIALvNwdYG1JM3gs3RA59mFEDJ2EaTTd9IOPfsDBAzvwx8Eo9AnpCQdFCyoH6JEdF4Mj51JwmWa+6I+uw4exK/DPCo0hh/Lnincew5rP3BDSaypee+8D/GmgZ+son2tyYb4vgtjNh/WdGxORKHeoLWgZJ3NK89MKaepE6hdj1uOb/36KXw/kIWjwHLz+75cwNdKjxWm0N6o4uvJ4LPn3GzjgNB3znp2K7jRl0/oKwEobD3TuNwj9u2zHye1FyE7NRSl1nxxuFKDZf7OAd9hgDBt4AhnFx5BeqIHFlfTrqypRUV6CErUSjs5OcHBwhLOjrVyHuBfY/PXI7GA1OEJB7A2GStzYOATIrssaOz1soWwhWrC+DOlntmPBfz/GzweLEDFpHt7559MYFGhXPQDQihhDqsxD4snj2JhcjogBPeDvagcve57JQ2MHRIzZSRcQn54Dtb0vzWF3hk2Ly5sFHENGYN6HNK7xLw00NA6goF4HKwA5Zzfi+48/wK/HHTD7zS/w+rT2UCosYUW9KSE3RkAQ+43xEb+aAAGJpjnqiNwtrS3J90rzM4u2MBUn9mzFmph8BA14FG+8/ggiXWmqY3Ex5ZZ6FUorWFlVk4uFhQJKmWiaP911FYWlay+MndwZKz4+jJ+//ga22nswolcwHGh+e/KJHVj60yJsOnIZQSMmY3DfjnBuUWYYoxxZWMLalo6aSxJUVgryb0M9PSoDlcoG1tbWrcrfTU1WmuFEEHszgH7HRUnEXkWZVlhbycTe7BTJZK20hEKdixMb3sPErR+RJnhtqdi7+MDLxwfB3cbgiT8/hpGRAXBqgTNKYOGEqAf/gtkxL+H7XQvx0u4FsrYr54ZMYHprT3QfNhuPP/kgRna5sgjr2qy22G8SpV9HB3X1qHFt9lrTYnGqK2GC2OtCRVwzHQKkial8umB4/26Ij+wKH5oX3tzvqJVLO/Sf+jBeyS3Dt4u34WKpEioF+bAhEvT1dpGnOOq0apQVZyMhLhk5hRWoaglzNOspFTv/4fjbFwvRb+MabNi8A/tiElBu64tOvQZixKixGD28H7q084Btq3FVWZ1RB49gdO0zHFF29ogMdhM29XrKv67LFjRPtKbKbt26FePGjZPvu3jxIkJDQ+t6RlwTCNwaAno1CnLyoLFxhbuTLSyb3RzAs3Q0qCgpQkFhCSr13OUn7VZhBRXPhiHtXSKfNnqdjq7Zwc3DFQ42Vlc14VvLvXnu1lfRQGMpysrKUV6urs6LrR3siRRtbVRkl259Gi8vGqsoLUOZRgFHFyfYkmlGCJCYmIj27dvLUGzZsgVjx469DhahsV8HibhgcgQUNnD18Td5sI0PkO3oKti7eMlH48NpQU/SoKKtg4t8tKBUNSkpchk5Uzk1KZQ782HRBN6Z5S5yLRAQCLRhBASxt+HCFVkTCAgE7kwEBLHfmeUuci0QEAi0YQQEsbfhwhVZEwgIBO5MBASx35nlLnItEBAItGEEBLG34cIVWRMICATuTAQEsd+Z5S5yLRAQCLRhBASxt+HCFVkTCAgE7kwEBLHfmeUuci0QEAi0YQTEylMTF25lZSWSk5Nx+vRpdOzYEd27dzdxDLceXHZ2Ns6cOYOcnJxbf9iMT9ja2oIPUwh7ytCRSwCFgtwF0NFQMfKw0dBHWux9jo6OsLGxqTd9FvV42qzvuqUluQOu4xnGmY/GCmOu0WjA4SuVpt2Xlcu+rjSrVCowPvVJfXWmvuucdj5qC8fNXin5qCsdte831ffrU2KqkO/AcPLz87Fr1y5s3rxZ/pw3b16LIPY9e/bgvffew9GjR1t0qXh5ecHJyckkadSTR0mtVisTRV0vXH0EXt91kyTKzIH4+vrWiyeTTH0kWh8ByW5z62gkmdSZmBsrXE7l5eXkmld1w4aoMeFz2ddFxkzq/v71u7mwsrKqk4gZs7rCY2zs7a93fsD3clx8uLm5oUOHDvDw8KgzjMbkr75nBLHXh8wtXOeKyVrx8uXL8e6778oVdO7cuXj22WdvIZTbd2tqaiqysrJMHgG/NPWRA0fGL+qtiFqtBh+mECYbfjk5DTdKY+246tM86wuDGwJuREwlHH9daeB4DAf3ClkM2jj7ka+rQWJnUeYQxpmJrS6pqmKHzdcLNwR1pZnvZDKsizw5nrrIk5+prwwqKirAR3MLN5adOnXCG2+8gWnTppmsZ1pfvgSx14dMA6/zSxYfH49vv/0WX9Deme7u7hg/fjxeffXVBoZw+2/jSmXQwlxcXGSNwRSxstnEzo52HapDmAhdXV3r+MU8l9LS0uSucb9+/a7zUsqkURdRM9Fwr6su4Z4EE0tt4YaorKys9uVGf+f4CwoKrnueyZ7jYpJisxoTGeeN5fz583U2BtcFcpsusDbKWmht4TSyJl6XcD4NDVheXh6Kiorg6ekpa7aMc11Yczx9+vSpKziUltJ+qXU0sHFxcbLSVedDZrjIeSwsLJTL9Ny5c/JmLvU1aKZMjiD2JqDJmnpsbCw++ugjrFq1StZaunbtivnz5zchVNM/yuRr0J5HjRol9yxMH0vLCvHhhx/G6tWrMWPGDLz00kstK3FNSM2FCxcwYsQImeA5f21BHnjgAaxfvx4vvvgiXn755baQpZo8cCP997//Hd988418jZUAQ4NWc9NtOGn4qNJtiLw1B8mtLmtOn376qUzqrBGz/YwrZ0sT1qbYvncnCWuE1Vvdta1cs2kjMzOzTWWqrZYVF5KDgwPmzJlTU15JSUmozzxVc5MJTgSxNxJEbokXLFiAZcuWySEweQ4fPhxTp05tZIi37zE2PRhMMbcvFhGyQEAg0FIQEMTeyJL4/fffsXHjxpqng4OD8eCDD9Z8FycCAYGAQKC5EBDE3gjkebCUpxBeunRJfpoHffr371/vwE4johCPCAQEAgKBRiMgiL0R0P3xxx84fPhwja2M9x+cOXNmnSP5jQhePCIQEAgIBJqEgCD2RsDH08tSUlJqnvT29kbfvn1rvosTgYBAQCDQnAgIYm8E+jx33bBIhAdNQ0ND653P3YjgTf4IL+qob765ySMTAQoEBAL1IsDz9c0x3VHMY6+3COr+ge3qubm5NT8ysYeHh9d8b9yJHgVJB7Bx3W6kIBQjJk9Av1BnmKrVvdkK0cal+eZPSXoNijPP4cDu3dgbfRSpWg906tYHw8aMQI8QD9hb1+0XRNIWIO7wdmzeeQ764JG47+6B8LU1FRo3T7fxHfqqUqSdP4oDe/fi0PFL0Dj4ILxnFIYO7o1OQe5Q1ZEFvU6NkuwEHN63B3sPHEdCgS069+yDqNFj0T/MEzZWNEvJOBKzn9Nip6IcxB8/gL37D+FkfA5sAiPRd8BQjBnRA151Yk3+XIrTcebYIRw8cAQn4rKgs/NF176DETWoLyJCvWBTBxbmyZoELaXt5OF92Lv3EE6naeAe1An9ho7AwJ4d4eOsusm7pCc8UhC9YgEW7dVg6guvYGo3V1gqTF9KvPbFHCKI/RZR5hVuxsveeeC0S5cutxjKtbdLmhyc3LEGy35ejXibfpB8uyAiuBscbkPFujbm2/dNV1mMlOPrMf/zhdh2PBFZOXko06uwZ8cWbNx+BE+98DQm9QuBm21tNpBQmnEOO9cuw/wlx+DWsxRdB/SGT3sbs5OhvjIbB9f8iO9+2YKjF5KQnVcCvaUtnLf8gT3DZ2DOn+7FmN4BsDF6/3WVhbh0Yht++f4nrDuYIOe7RKPEvn1/YMPmfXj05Vdwz6BguDQXC0qVyE85iW3Lf8HPq/YgLjUbBSVqKOz3YMfmddh96kW88dxY+NmRj5Wa6qFH0aWDWLFoEVb/EYPzKfRMcQUkpS127vgDuwZNwOw/PYKplK8624SacG7HiYSyzBgs+fpLLNl+AomUn8IyPWzsnbFl225MeuAxPDh9GDp529Vbf3TqQqTErsdXn/+MnWmW0A+cjfFdnInYa9fN25H+2xOmIPZbxNXPzw+8LN8gvKze2dnZ8PXWPvWVKMrNxPlDa/Hbqu04Ep8MtUcQ0tPzUSHR4oZbC63F3C3pypGftA+L/vcZFu/JhHfPUbjvrhC4qiqRdnwH1h9YhV9XdkZH0nj7hJBmJKdcQpW6BLkZ57F37VKs3nQACSnFCPFORmY+OZgiYjerSFok7fsNX3z9C/an2aBzr3EYF+YHO/1lnNq/D6e2r8Zan2CEhZIG73blNdKXI+fiQSyf/zV+3ZYAu45DMGNSGDwddLh8fi9WE3H+uLAXIjveh54BzrAyahDMkzcJFbkXsW/dL/jmp81Igy/6ThqDMF8HaPMTcXD7VqxZ8BV6D+mLh/u5w8aymtp1xfHY9PP3+HHpPuRa+6Hb8CiEBbpCWZmHhOMxOLN/DZbYeqJd0GMYEGQa75wNw4P89FSmYev3/8PXv+5BmUcPRE2ZgBAfW1Skn8Cu3SewfvkGBASHIHBMOByUdQCuV6Mw4wQ2/LoYu89eQpGFMxIvZqFC1xW25EGijicalrRmvksQ+y0WAPs/4dVkTRapDHF7fseSVTtx4MhRnE/OQkmlElZVOtkroencSkF2OGQqd7gNyXdVeSGSjm3H6j1JsOl6P/7y6tMY3i0QLioN0g65I/38xzh58AQSMkaiWzsXucurKYjHznUrsW7zbhw5lYBLafmwIm1er68iPOp2JNWQtDT6Hl0GDqxehwMXtOg69VE8/cgUDOzkBxsi9n2+Wnzw7U7Enz6FxOzRCHNzlglAV5GPpJP7sXFvPKSgcZj7yvOY1Kc93OyqkH+hPXKO/h1/xBxAXMZkdPYl3zOW5qYNLS4nHcf+nfuQrPHA2Efm4dn7ohDiZYvKy+exXpmCv3wRg+2HL+G+3m5E7IyeHpmnNmPVhmhkqzphyoMPYdaEgejg6wylNh9ndvyCL7/6DceO7kH0+SnoG9QOZtNzafW3Ou0Qlq7chzSrbnj0secwe1xfhHjYoCJzH+wK/4NfY8/h7LkU5A/tCAe72ikjXzaFKTi8ZTmW7IiHhYcP3EqLUZSZixK9BPZ0ZOoSYt85dfm0aXQ9redBQez1AHOjy0zufNTlrOlGz137GzkHyriIuMQ0lNu0w4ARnZEfdxoXCsiL37U3NvkbewE0+IppcmA3DYA0b00pMpMSkFlpj+HjZ2Hq4HDYycqfHXz8fMgMYQltWQXUWh3RRrVIlUVIT0pEYnopHIN7Y2hYKFLOn0Qe/WxqPG6aBbpBr85C/NkMVKjCMWLCGAzs3h6ebGegxHh6OMHOmsi6shzqSkMOgKqKYuSkXkJamQphQ6bhrhHd4MlquaSHV0AA3GhMQZtXhgpNFYg3zC9SBQpzUpGWWQbHgMEYP3UUugU7EXlJsHb1ga+nI5FyFYpLycxCpFktEsqL8qG28UW/ETNxz7Qx6B1KjTH/KFnDP8AP7o5KVKYVI7+EnrvylFk+CNfyjAs4l1EGr+ETMHnsABr3cJV7QrY0U83dwQYKLZVReSXq0g2qKnKReGQLlizZhXSLjhg/OQhn12xGXk4+ynSmfw8ZE3bidhXb24eSIPZGYMvz1n18fGRiZ3t7o3ySWNgiuM8EzHHuBz0NQgW55GLDt58hfRcVPL31Zn1BGoFB/Y+Qn28rB/iE9cbo0b4YPbhDjd1VV56Og9t24OxlDXx6BcPf3QHW5GOHxdKZGrfxs+HVswJOvoFQ5mzHL18l4Q/aG8QcL8J1+VG4Irz/QIzp1A99w73haMMtEzXGKccRc/g80kpt0c4/CL7utjVancLaCT4demLkGDt0HtYVrrKthTb8qLyMo1s2IDa7HO4dwxDgbgfrZhk/sYSTd0f0GjwGPi7DEOFvX93T0JQhO/4gtu5OgMaxHbp38oV1jdlCAc9Oo3H/YxHwieiHzv5OMqnrtaXITjyGP7bswtHECjgHhiIswNXILn8doqa/QHXH0r0jooaNgP34/mjnZgfuBElVxUg4vB+xCVnQOxPegeTnXy6/q0ng9GfFHcSaJauwL1mBvnfNwSMTNfho0zakF5VDQw1b630H6X26mlVx1lAEeGck3sSA3XDyYCr7Yr91sYJX2CCMDat+UptziGx6CpnEmNhbs1g7eiFy7JN4o0spPNq7yxphVVkmYjb+iK8W/YHLdh1x76TBRBKuROzVOVXaeqFLfzrkr2Tfjj5Q3aXnF6xGezQfKgrb9pj057+jj9YFft6uUJEmW5h2EpuX/Izfd1wEfPth6PBB6OB91ee8laMPuo98AH+PKIaND5kkSKPUlGXj1K4l+OTLVUiyDsWMWWPR1c+pztk0tz13FnbwjxiFB317opwMDQFOCmp0SpBxfg+WLfgea2OLqacxF9P7B0JlaTBbWMA1dAjuDTVOXRVyE/Zj5c8/YuHy/TTbyR9jB43GoE7uZiZ2JZw6TsArb3eFwisUXg4qSNpiJB3dhIULluFQpgXCRw/D4D6hcDVUNM4GjZ8UZpzG9lVLsHLvJbj3mo1HH52AcN0W0vYtCBMtdK38HRTEblxfG3jOxB5AXWsWdsN5+fLlBj7ZgNuY0+lo1dRuYQkbJx+EMUsTuakLknBw48/47PNFiMlzx/DZT2H2+B7wd1XVaLs3QqYZeJ2Mq0o4+3WEPCxOg9y5ZJvetPgHLFi6F5mWHTF15r2YMrwr3I0Jg/Jt5+yFYDpIbUR5wSXE7vidZlt8j+3Jthh077N4fHpv+DrdbPrdjdBoym8WNG7hDG8auOUapqUxgcQTu7D8px+waP0Z2HWbhD+/OAd9/GlzkisNbp2xETHmppzB0eM0xnC5BCovFexoPKRKTZtnONP2eXU+dHsuKqwc0a5zVzlwnToPF2I24adv52NNTDY8etyN+2ZNQN8O7kYabBVKcuKxf8MyLF57GKWe/fDMEw9jdBdXFJ5gJYKQkf/wJwVrzsyYECJB7I0Ak2fG8G4oPIedNwnglahNFa5DV+pTU4O67nnjjTau+/E2XuB57CXZcdi3dgE++Wwpzqp9idRfwF+fnIiu/jeeFSKbo1pA68YzfDLjDmHNovn4aWUsCh26YNojT+KRmUMR5lF3w6TXVcrkcWDTYnz99WJE59ghatZf8I+/zkSEjz2oY9a8ItE89pIcIsEtWPzjQizfdQnOEZPxzN9ewX2D/G8+W8fCGr7hQzF1ehEk1W7EnEjBrmWL4O0bgHn39rpigjJnFqmRKs3C6X2r8f1XP2DTmWIE9LkbTz3zCCb2bw9n66uAS5X5uHBwE35dtBoxqTqEDw2kQdbjWL+SZsckHUUGNU660nPYvmYlEp3cERgegYgO3nBQmabBYtOtOXqggtgbWf8GDhyIHj16gP3G8OYHvPUc290bLcTqeh6w4bE4E2sJzbFASV9VgYLU09i27Bt8/NUapFuFYdoz/8ALfxqBULIxN3xCCO/+1GhUm/Qg22HTzu3G4q8/x6KtF2DhNwhznnoa90/sh2C3ekid8p2fdga7Vv6Er75fhQuaAEx89CX847m70MHVCs1iWjdGgUi9vDANJ/eswcLvfsH62CIEDrwXL7z2HO7q41djGrv6iB5leSlIy5XgwgOSzlx2tDtWcB9MezwSQ8aMw8pvP8FXS05i+4ZdmDwuEn08zUkrEippcdKxbb/hs09+wP5UBbqMfhRzn74fIyID4FCrFdWV5yE1IZ5moeXToHA5Tm39Gs+v/BDVmw1eyfXlxXj1kcWwsG+PCU/8E++8PIXMZ45GWv9VdG71jH3Pm8MfuzlL4FYxaNH3sxsBNsns378fFy9exIoVK5q4xykP1kiwoDefj6s6RouGoc7E8crLgtTjWPPdf/HhD7tR6tEPj/3tLTw7sxc8r1n4Uufj1RflLjGdEqk3iy95fQUyz2zDN++9j2XRGaTRTsETzz2Nu4d2hpd93a9Ndb5PYOPPX+LzBTuRY9sJ9/31dbz8yDD4mH/lTh3g6lFBKyyPbl2Mr77+FbuSlIic/CRefOlRjAyvZ+CTFjTFbf8O/11diL4zHsGscT3g63Al/xZWcA3ohB59IhC64zgSC1JxuZA0E886or4tl2gGVkU2Ytd/hX+9uxgnC50Qde9zmPf0dPQKoXn4hmECo7iV9t7o3IdmBI1KhMXxNFTW9AppkFtdjKy0LKjtaTKDD01HVXjDmwZkm2eg2yjRjTitu4Y2IqA77ZGgoCAMGjQIO3fulAdPjxw5IvuPafS0QtbYmcyYyGhjjNYrRB75Sdi75FO8N38X1O3G4m/v/huPjGgHW1rwYsH2ppuq4NWNHLVzcudFcdP7TY+WOvcoFrz3H/y0KxvBQx+hnbEew5geAXCkbn3dWaCxhDxa/LPqW/zvuy0o8ozC069RYzY9Ao5ksObud7M0UEbQSNpCxEWvxXdfL8LOS7YYct88vPbCvYj0oVW9lD5KYR1FQ9Mfc5Jw8gCNLdiFonNHfziHe8iDv3qdlkxOCTh7+iJS86zg1D4Q7jQgay6RaOwj/cACvPXW9ziuDsZdz/0f/jJnODp4OVCv4kp+aiXGwtoNnYY9iP9E3Ys3aZBUTyqUgrtRmhKkH1qABx96D1ndX8Tvi59AGA3G2li3gF5WrTw05Ksg9oagVM893bt3l80xS5YswalTpxATE4MhQ4bUc/dNLpMNRn75lQrahFlpUo2dF0SYY1GEnEN9GQ2sxWLj8mhcVoXhsT8/h0nhSuSkpcg/W1hw/qxhaaWkDaWtaem3HexUVlDWtlEQHpxm7r1Y1upO3wRJE/ysR8ahVViyOwnWoXfTyz4RXdx1yMtIQS6Rn4KWmvNmy1xOllb08tPqY1uVFjnJR7Fzyx5a0RmIGXOewt39nJGfmkxz8bkXRhtoW1rSoiTKq9IKKlt72NPSxuvybYLU1xeEJpf81+zeg/3xWrQf8gAevncI3CqzcCmZn6B8KSl9RGSWtBG5pbUNHMh5nJWlA7pFjUH3pcewa+fv+JGIu2hCfzKnWaP8cjyit6zGyo3RyHKIxOzRQxDuWYeaXF+CmnSd6oc2GzsXL8HBdAsMfuIpPDAuDCqam552iSYzkLlISeVTjbclrFU2tFCP1nNQveO8ct2ztbOuSYFkUQkrJSlXdEVprYLK2prWfhCp19xhmhNzOADjlApib0J5MbHzrunLly+XN9345ZdfMGDAgEb7ZZeoFlkwYVgZ++loQgKvPMrz7EtKSpoeUENCYOK2IsImDwDlOTH4+LHB+PjKcxZEiMzfCnsXeLl7wdu/E8Y88BQevisK4df48qCFS3IXmQhGQTvWE9GYW5RWtrCjckiKWYA/T/vBkAOZoBUWNrB3doKbhyeCOg3ClHsfxkN3dyNiJDKgxVfFWScw/68T6Kh+rCbfDk7wdPOCJ03NGzb7OcydFYUOPg4mJ496saIGxVpFM14qsnBw2ZuYQocs1CPi7RMVVHaO7v7w9ib3AJFT8OLf5yKqvRvc2Az10HGk/W8VNn31N/z+GTe6EuWXydMW3qF9cNfDz+CpGb3hXLuBrjcxpvhBCZWdit63Imz97Als+exKmIb82NjD1cUNHp5BiBxODfScWRgb6VP/+A51lyV6Ca1Z0aB6ejskIyND2NhvB7CmDpN3Tho5ciS2bt2Kbdu2Yf78+Y2ytSsd/dG1ey8MU+oREe7beh2AWdjDu+MoPPPPV1HxwVdYFZtHLoOVKCd3Cb7+vnB2JGKhqYAVJYXIS7+E9Iw8lGuurt6sLh9ruPqR7XbgaGhyw9DR19wOwBQIHDEX779ZiQ8/W4aTeTpaVqqB0o5WHLu7wYnGCfh7Ga3IzM1IxqWsYmglG/h1GYmHXyihOeLfYsW+ZGrAbKFVS3AP9JdXQcr5Li/C5bSLSMmg1Y208lZuv0xdKesJT+XZBeMfehIVlVX4fsVepJQTiVF9g40XzdV3IlOZBapoNW1RfjYS4lKRX14FHdudrDww5NF/Y0GPUVi/dh02bt2D89k6uIX0xLDR4zB+3EgM6B4MZ5Wp9dt6MiJfph6QtS+mvPxfZFb9B1+vOIEKa1rRrAYcabaau5sjeE2StrIMBXk5SE9JRV6ppmal83UhUy/SqV0kxg0dgFxeMUyrhM2Zm+vS08QLQmNvIoA8O2bSpEkysbNLX9ban3322VsOVWnfDqMffR3D6D1TUiVT3SaN4ZYT1ogHLG3dEDb0MXzS7368T15KFQoeP+Dub/Wm2rI9lwiDr1mRas92zGuzq4R7+6F49LUBmKMnrYy9MZlZFCofDH3wbfSb8RotTTLYyCn9pJHKJn9mZLZLk5ZrRd18GyI1BciFc9RDeL/PPXhbS9ZbYga9nvLNYwv0ULUdm57hMlax+YY0Q3Pmy0IFz/ZReOStPpj9Gi3CIfzZnYDEZiJOHxUC87jEZkEaGLW3oxkwV6YvKcgk0673BDzVbTQeeYWmBFIeLMh0Y029MysyMXEezS5kbnHwH4S5H67Ao/+miiann/Ih9z7kr5w7GW8Fv1NU14yXHRin14I8VbqEjsY/fooiD5425DJCWatOGt/d8s8FsTexjJTUHWWTTFRUFLlm3UeeGdNlrf3JJ5+8tZBlgrCF+Sns1pLZsLvZrYAK9nw07IHr7rJQEGmQWeOqFfS6W27zBbLtE/k60NFwqc63HeXbruEPmfVOGVdbcuVwK9mSU8gNMzVE1MiqbFtQ7ngxnJ0DHU2HkbGxtTeBg7+mJ6XJITRDM9vkNLe4AIKDg9G7d285XexeYMGCBS0ujSJBAgGBwJ2DgCB2E5Q1r0TlQVP+1Gg08n6oX375pQlCFkEIBAQCrR0BHpjmDXlY2AWJOWaoCWI3Qa2xpqlR7PGxa9eucmjsZmDhwoUmCFkEIRAQCLQFBHj1N4+zmGPVKeMliN1EtcbLywvdunWTQ2OtnQdSeX67EIGAQEAgYG4ExOCpiRD3Jj8aERERNaGxO9/vvvsO9913X8215jrJzMxETk6OHD2vkJ05c2ZzJcVs8Z44cUKOa+nSpYhjN3WqAABAAElEQVSNjTVbvLc7IsN6BN6Jp65y5HpovPqZe5OsLbYk8fcnR2O0XsMgXD9ZuMwWL15suNzoT8bAeMcwxuNWMeAwDOLm5nZNeg3XW/JnyyrxlozUTdLGuxQFBgaCKy3PjOGdUthfO3t+ZE+QzSlcyTl9LLzyjRsdPnJzc+UxAV7xyt+NhZ0VmcMWaBzn7ThnsjCQ/O0Iv7nC5F4h+yeqLbyzF8/UMgifG383XG/OT0dHR3lBlCEN7ECPZc+ePTh9+rThcqM/OXzjhoPzz3buWxEOwyB2NO3zVjDk943derPphc/5PTK8f4Ywb/enIHYTIuzu7i6TOBM7kyWT++7du5ud2HnzbScnJzmn7LjsH//4h7wS1UDsXPFq7wLFmmFjiZ0bD4NmaYC3sLBQxsTw/XZ/8tRTNofxbKWGNKyc5tp+9Ssrr/H5d7uT3KDwuU5xD4SJixfHtQXhMSkW1qyNCZWv8WAjKxm3IlzXmlO4l8T54PrEhM6N7a32GJqafkHsTUXQ6HlunQ2j33xZq9XK3h95TntzO4AyJJO7lY32Z2MI5CafTJJFRUXX3MUvLzd25pJnnnlGJvYRI0bgiSeeuGm03Ijxcm9jYWI3Z5qN467vPCUlRSZ2JsHXXnutvtta1fW33npLNhUOHz4c06dPvybtrCA0boeya4Ix+xeuO1yfuP5wHqKjo82aBkHstxFuHgHnF/FOE+62cgNiLLW/G/92O865+8zC8YaFhTUoioZo9g0K6DbedObMGTl01gAnTpx4G2MyX9Cff/65HBmXU1vJkwE9Vu7YFGjucZ5bMzwZUis+BQICAYGAQKDFIiCI3YRFwwNaxiYI1lzZ7i5EICAQEAiYEwFB7CZEmwd5jPc/5QEudhLWUuzrJsyqCEogIBBowQgIYjdR4bC2zvNxk5KSakJkYh82bFjNd3EiEBAICATMgYAJB09pz0BtJcoK85BXUgFNpQZa8u3JmwxYsWtP3pHEhjYvsKOdY+xtaAMFdhnadoRJnXdQMgiTOi9y6Nu3r+GS+BQICARaOALyLCiaf97aucl0xC5pUJh2AusXfotle84hLSsXBcUVUFg7wMXTG76+tEFsSBi69uiHgf0j0SHQmzYssL5tO5WYs/7wyPfRo0exYcMGOVpeDMH5ffPNN2+QDNqIV6NGRXkZSsvKyTc2NYA2DnBwsJP9dJtyIxrzT9mrbuQraA5yKa2QVGstyK2qHRwcnWgbPNodqtZbo9OUo6SoGKUVlaiSN35lL9okNFWM/Z1bEi4uNBfYqa7diW+AsGl+onKqVKO8vBRl5RVUTrQLEfmItXekcrrRfpjk01yrLkNJaRk9S9MmleTjm8rWnrYC5O3ZakFgmqTeSiiUvipSxMqpjMqojDQ6JW0VR0oXzb+2U9VKn0R7mxYWoLi0Atqq6i0c5fKhXHBdV9J2fzbk7tbRgdznmn0bw6uZ1usqIdc5ep9oLxHyk09ulylNtja0+rZ2pePHuIw0FfJc+fJyNTT0HmvUGihoQxV33lDF3vT8xLO1zGGaNRmx6ysLkHxsK375fhV25eqokK2rHdGo1SgtzkVqwikc2r0ZizUW8ImciMfmzcP9YyPh76pq1Q5rmDTPnj0rb48XHx8vV3TW1GfNmoV77rnnaq275ozIQp2HuCN7sGXDWmzafgRZWieE9BqFqXdNoV1cIuHnbDpcuOHhwyxCL4umogDp5w9iw5rV2LBlP85ctkPkoGGYOOtBTBvaGd5ONkYNuh55Fzbhq89+wBpSCPKIBKtoZ6GqKtoej+bD62mDB3+qL8+98QYeH+pv5rpC5UR7aJ4/tAMb1q/D5p1Hac9Td4T3GYNp06dg1KAu8HG6vpwkfRXKClJxYvdaLFu5BXsPnUOFaxcMpd2GJk2bjEFd/eFmT881F7tLOlSWXMbFk/uojNZi865YJJe6oOeQEZh874O4a3BHOFMjakheVfEFLP/wHXy/7hCSL5ehksyOVTpJ3hDGxt6RFLcg9Bg2BQ89Ngdju7qbuYyqa7VeW4GsuAPYumEd1m/ehTM5SviF9cOE6TMwcVQ/hPk4ErlffQO4jMoL03D20B9Yt/4PKqPjSEjLRWFuMZy7jMODc1/A07MGI9DVuK5efb6xZ+wo0CyrUImYamTLli3cEMvHxYsXa6435KSqPE06uOR1aVhQkBQx/kPp8OVCqaxCLakryqXigstS6sUzUvSWxdI7z0yUwrxdJb9eD0mfbzwt5VfqGxJ8zT16vU7S6fRSg56ijRmJHCRafFLzvKlPaMBUIs1cxoxaYolcCkhvv/32DaPRa7KlvT+8KI2KCJCcba0lWqkmH1a0m653+HDpuU+3SenltCmZiWT79u0Sbd8np3HGjBkmCrWuYPSSpiRDOrL639LUHj4SaXKUL5WkUlH+rCwlK7cI6dlv90upRZVXy09fLO3/4UlpWFcP+X4r+X5+pvqwdfGWwofOkT7/I0W6FUQmT54s5/edd96pK6ENuqbXZEo7vporDQ7zkZxsOS9XyslSKfl2nSC9+t0eKauiVqr0GqkoPVb69f/uljq4qCTa/1WifUary5eeswscLD3/7R4ppUB9FYMGpab6JlpyL+eLVhPfwlPGt+qlivwE6Y8FL0mjO3tdKSNriTZvpjTaSnbefaXXVsRJJZqqmocqs3dLb87oLbVzt63BwIAFlys1UJJHx8HSY1/sk4ro3bxVGT9+vJynDz744FYfrb5fr5WS9n4u3T+gg+TuaCOR2bc6nZQ2a8/u0qxXF0mx6eVGeOuk4oyj0tL/3C9197KtLiN6Rq6n/Cw9p3QOk57+JkbKLDaqq41IHY29SYcPH5YiIyMl5gcyzUq0cKkRIV19hLnZwNPM2XWJURvW2DbI8BxvrUVdMz5og1snZ+rS2dBu32RXd3Rxh39IZwwYPQsvffgp/vFgD9hm7sMh0mTS82tpkqTx8cpFuUtuCFr+ZC23CBejV2DBskPIrbrSXTf8pqmirdauvVaYehTbN2/GrtgkFFMX0tSipt7IV199BSIPOWhe4MJ7nvKS/fpFj7R9P+Gd/y3HqUI/TJn3OdYfOI3zZ6Kx6F9z0MEiEdGb1mLfuaJqc0T9AbW4X6SqEqSc2oxv35+P3al2mPjs59h6+BySk85i2/y56K5Kx5of1+BYSgHUNcWhI381tLemzgEjZ7+BNTHJtGIvUx6I5nGL9KQLOLxpPp4eEWBmTVCPlJ3z8dZHqxBX0R6zXv2e8nIW50/vxfev34OAyjPYs3kTDiUUG5UTuZHIv4i9yz7DO9/ugTZ0Ot79dQdOxSXg7MG1+OSVexCOi7RgJR6XS9X17795G0tW0ubj7N4V+O6LJThR6oNZr3yPHbEXkHD+EFZ8MBtB2nP4+dMVOFdIY2RMHyTWnlF4ef567I09Q7O+LuDChTjExdFx9iAWf/Q0Rnb2oZ2HnGnfVDfY0vtvbtFkbcfHf/8YW+M16D3rTfy29SjOx53G1h/+htGBpYjdvQXbDyei4kqd01Vk4OTOVfjhp93IdR2EFz5ZiYMnCYP48zhBvbPf//sIwq0zsfGXdaT5l6DyCg7mzldT4jOZKYYTIduOCIRK2pz4WiyY9OUbyJmOAtQLIvMW2eZoYNVQD/TaIiQc3oplP/+MVTtP4bLGAe0jB2HMlOm4a8JQdPa1ou7tGaz+4l94/4APLMJWYU4Pe1gpdLi49X28/NZWOI+di3mPTUD3QHIypMvG4bU/4MMfD8Mx6nG8FvAo+vhQ3NpipF84hHXLlmPz3uNILrJH5z4DMXTkGEwcNxjBrrX336wb3oKCApCGIRM7uxKYNm0avv32W9mmd0OHQbp8HNuzE4klSgy67yk88/h09G3nTFjooRo5EvujT2BzVirOp+ZA34scOtUdfYu8WlWWi+RTRxGdIqHDmHn41z8eQlfuyippQ+e778WY7zfi+9TzuJRZAnVHLxpLoEpB9lutmhplhT0cXL3JJYM7+da4tlrK9crcOdbl4siOHUiutMHIx57H3D+NQ4SfI5VTIKzGjMCufWcQfTkF8el50Ee4yOUkaQtx6SQRw297kO/cFy/86z+YOzoINpZKSP5eeDS8P6Y9ehmSiy+8nO2bpWy1Rem4cPIUTuQ7oPvk5/H6izMR5kJlBG/YTZuO0Qu24ruk40jMqkSEK23VyEVB4xz2VDa2LsZvtYTCOCL6k2cQV+iE9mNHY/yAEFiZndf1SI/djp3x5fAb9jz+Mu8hDOlEDY2STL5jxmLotv2Ij85B8sVsFOu6wI66FxW5ZII5fgrxWm8MeexF/PXhkfCiLf/YNKb39UO7QDW2L9iARSnxSLtM4wpBEo0dmD1jTarx175BTQhK1tZpIEVBlK5n+6ihDpAGXllRhKLcbCTFn8a+DYuxcNUpVHiPRmTP9vDhl1hfjDPbFuDjT37CRmpZi2iQRkPEn3s5FWdi92L79gfw938+jwGuHggMcoJ2/TnsIy18drfOsNJfwp6VGxFLYWtKNqH/wO4I9g2HQ0k6aRTJSM2zRC9HD7g4UOdEKkPKsQ346v0P8eOuJKgr1KjUKZCceBw71/+ChVFP4cP3n8egdg7UYNQPxt69e/Hpp59iB7347Oxn9uzZeOmll65bRl93CCXIzyqFRhGAjh07IMDLiV4eTpsW5SWFNJBaCYUVzR5SWdfYOOsOp+Vd1dEW8TzIViZZI6xHD3R0o82Q5ZaJBlOLLyO7qAJVFrShMA+gGvCVKlCcx3ZbmjVFe2mqrKj+kN8W3opYwZtfN1c2pRLkZpaiShmCzp07wtedPAbK5USeMIsKaFBYA0tq0O1oQ2pDGtUFGWSzjca+dCBs+gO4d3gQbYpseMVoII4mC/iFkDM2IkqDQmPu7PGAblFhETRWDgjpHoEQFyojrn5kM9eV5CGzWE2bW9uTHfiKMmZIICWYe+MG0ZXEYff6Ndi09xJcu4zB/Q9NR0/fag+ihnvM80kNTG4GyquU6EFus0O8XWEnD05TfkqLUUBcorOkgW472q/1Sp3jDckVFtS715ZBXUT1Mr8CngEquUyUtEG3kgZhy6m7Ilna00A5KZ+GumqeDJkkFkOta3pgVOgWhICiqhzZJ77DY2OXQkOOoMqpH0NGbtrVvApamgJZUa6FW9hIPP3k05gyoANcqCUsStiPlb+vQ/QlBXrPeAX33zUYQQ5aZMUfxuaVK7Blz1J8+m04Ql+NQniPnnCzOo3YXUeReV8YvHOOYPuRNBSTo53ismjEnkjAiN6hQHYyLqRdhtrJD4HtA+Bhq6CCzsGF2EM4cKoE7YjEX5g7Ee3ttbh86Qz2rluMn7d+gdffC8YPH8xAexq8rEtb5pku7DOa/ZvzIAgPkDKpG/tvviGYSl+MfPQlWA5RoeuALvCy41j0KLp0EBtXbcaheB0ChvdE73BvM5sebpjqBv1o7RSIvpOfwvve4+E5IBLVk1ho9kXpRaz84hvsSi9Hh/FD0C3IGXaW1SSh11BDl1sKdSmZ2Q6vwvt/XYm0hAxo7dph0ISpmDpxJPpRV5+Ve7OKpR/GPv0qrMc4oV9UKNyo/nA5FSTuwerl23A8zRJhk3sgMtTzSjnpUZqfhnjqzpdbe6B3nxAUxizHso3bsPtkLlxCuqL3gCEYM3owwrwdYX0l/2bNE0Vm6xGGUfc9D/fexQig+qfibPGsl+zTWP7NAkTTxIdes0ejq5cNiB/rFlKQLkRvwNpN+5BlG4a7ZtyLSf39SUuu+/bbe1WBDqOfwdvvjEHQ4H7wp94HV5Wq4nhsWb4Mu05lwjV8MHp2C4YzafEstu4h6D1sFIbFxGPzojdw/x+L0G/kOIwe1gsBqmzsXzkfW9IqEDZtADp50UwfVuWbKGxeZrG3tyeebHp4N0uOyYidk1rdElahhOyMx2PIJq4lOx2ZXYxF6dkXd898CDPG9EY7d/JzjBIkxO7CkXOZcOsyAbMfnoNp/fzpxSdNv0c4/FwUKH7/OxzbvRqHHxj6/+19B3hUx9X2K6167733XpEQEojemykGTDPYuBH3xP6SfHEcO4kdx0mcD2NjY2xjuimmmGIjQIDoCBBVEqCOCmqod2n/c65YsRIrUFmtgP/O81zp7r1zp5yZOXPmVMQGDECE5Y/4haTZl3Inw+l8PC4XVFL0dCNIqvNxgY5Y6QWhaM65hrzichjahMPd1QYGNKhSQR2qCpV1zdDRNoC5tRO83KwQEhyCkJBA+IQmoNLdD+Za5L9ZvtF37999912sW7dO8DbHVCW7hJ0+fXrXkbpQjg7sg0j7xVuNKFSiXomVVJp2FBu/Wo61v1yDtsdIPDVzAsLs+4P6UdDpbjxi1VZrjwhMsA8m6tQA6qR9UVuSQuyzD/D3dafR7DYBzy0eDW9CbK14TYq6gkxcyy5Fcdlt1J4/jPSkZtRU1aBFMwU3Uy/iZPxxzH/9TTw72hMCbu1Ge3qXVRdOYeMw3V+dbC/I7kKtGcWpB7Fm+TJsik+Hif9kPDV1FAJstFurIXXfGqJ4CwvKUF/Tgks7PsOrqeeRcaecCI4maJw7gyO/bMGP2ydj6du/wZRIF5i07ny9a2Y3v1bXNoVLYDRsvZrpxEFIpqUOpdnnsHn5J/hs+zXoBM3GGy+PgL0+UbgKy6YTS845/LIzDonZRJyMm4xp48JhTfn7J6nBwDYcU54OhCapa2oTodhwJwV7vvsvPt+QgFKTUMyeNglDAqyhdbeB6trkXjtmBt4gWaD5ylVYu/sMfs5LwZGderQem1BVVgmzqOfw9suj4WFBOEqJeJjVQx8rxM5HZ6bY1Uhf18pzKBa/OBIuggCV9o7GGtwpzMGVk/ux90QuqT2ew9ihoXCxJh55yx1kJWeisFQfzrFhCPW3gyEd1TnpGTvAOygCAwN30AK/jqS0coyPDcLgCEts3X4CR+nY6xx/DkWNxoiZMAglpD6YdekirqQkoyIjHYV3AGtvV7g7mINLlOpZwZP16P0vYN/p1fj9kj0wNbGBR2AIgoL84RU1GX4B3qTqRfEJhRa0/0PSZ4FN0MoqgMBP74kvGAltKqQlRw2qQ97lOKxdsRKb4pKh5jgEzyxZhKeGeMBIS9HW0r49j94vNWho6cCArpbmOtzJTMTG5Z9i2ZbjqLUagVfeeQOTBxLl1AZfyq9nATcvV3gVa0LXKYAMuoLhaW8CaWU2zh85gMO0ga9bZQpnl99jnLeBwnHpKzjwONHBTRinnPN78O3yldh2JA26XqMwf8l8TCCesmHbONGJlFTuaqtZ57sYSadOQs/MD5NfGIcB7iZoKMlC0ok4/Hp8K/7vX3ow+eAVjAy0g76qKXdao5raenTR+YNOS7lXj2LdF5/ju32XANp43/7j6xgbYElygU7mX1MpLsbvxsGTNyBxjMWYiSMR5ECyh74ahC6UyzjHiCh1GihU5yVi6zefY9WWBBTq+GHKgucxe/wA2BnJ0DplU6PgI7QBtNTdQV5uAapaiNDTMoKtkzUasi/helElNImzoE0bhYSodUW4oAvN6tcsSqPYhd4L7BhN6FmEYdK8BQgxJkqH+aTEhqmtLkPBiCAY/+2v2HhhF+KOR8Pf2RIexk2k90y6y3RS0ZBoCvnbIEKTUEOLjDoMeBaSEQUp0GjrO2AgHZksN21H3NovYJKZgSaDwRg+fSaqNTPx3YHLOJ9wEJm30lFcb0aCSeJjW+oKRapp6sMhYDjmLdWFDwl9bmTkIDevEDfP7MaZX3fQMdUHM3/3F7w0zoMW7D09Xll7Fi1aJERE4XBrrBVAakek2XMafn5+sixd/t9CGiRpJ7Zj1Yof8PPpPBj5jMacRQsxbWQIHSeJ39flkh69jM2EMPKuHsTqz5dj/YFrgMsEvPnGq3h6VDBsDdsbfWia+mDKkt8i+Kl6aNMm6+hgC3Pa9aT1ZYj0sYVO09fYcjEeexKmYahnOAm/VNtfaVMFUo5uxlfL12Df+SJYh07C3EXzMDk2kHTY5eQghCw0NLRJfkBSJg3a3Jyi8dxrSzGHxtPBTIf04e9g1IhIWH/8Hr4/8TPiTo5EIM1/VzM5hKPCrrF+/s2ze/H9V6uw42QO9P2ewsuvvYwZw7xhQptVZ/OvIjsRB+JP42atGQZOHonYMGfVb06K4ESnw5Kbh7Dmi+XYsCcJddYReHreYsyZPLhVh12+Qy3VyEs+jp0bfsLZAgPEziP7inGEjxyNUJN1Ej/RqXx74m58t34IfN6dAE8LfYEwVFTto/pMeYj97lRgAYuaREuwYNNvY7ppCdZ6xqbj8PS0Qzh48WecOX4eN4cHw8lEH2a2JPDQuow8kkJn5lbCy9hEYIW0NFaiiLQoLl4rgcTAHe6ORHmTYNE1MhZhtrtx7Pwp3KqtgPXICAT5h0KnKhS7T+xC4i87SE5ahkbLaLh4OsOKBae0m1fmXcXBXdtxJMMYo2cuxmSjegoPV4TCvHRcptPExrVxWL0qBqMGOSKQjmAdiSk2LliyZInAW1+zZg1ycnKwZcsWuLm5dcsnTEsDUT1xG/D1yvU4dLUGDgOmYu6zszFhMBm8KNEwSTbp2C+8aqKjs0FPibBRrlr+HXadyoJJyEy8+JsX8FQssbhoPnRkL6oR+8bc2gEaZpowMDGFse7dKalpCfegSMREJeDA2WNIuZCGOy1hglaDrF99/b+loQjn9q7Bl19vxNHrTfAYMgvzn30aYwZ6wsqw4+ZL1pcGZrC0MoYxIfzA0XOwcEoMnI3vsih0bEntdwQmjdmCLQlxSL55C2VskUqIXR7n9HWfeB00VJC635Ft+HblRhy6UgLbgXPwwkvPYkK0F0wFprviVkiJWr9CqoPHL+TCwGU8hg6Lgpt5K09b8RcqeiqtR27SHnyz7Cs6Ud2ADrEzFyxciOljBsDF0uC+ddxcU4z0S2dw9GIRDHyfxtI3X8ZIv9bTU1OoD1zsDFDx1t9wZO9OnJ0WDQdjPRj2QiuG+euyKFAcIEUVrBil0j8CK4bGkg45bA1+f1I3hG/MMITY6uL2tYtIybiNqmZjuAayJosOaawcxNYfd+FoUioy0pNxNn4nNqzdjCPpjXAMGYFBXqTGSJuGkXMECUgt0UgCt/I6A3iF+cPe3BI+ETHwtzVEZW4aMgrqYOHiAV9Pe4G/zo1pJHW8G0nHsXfvXhy/WQMLEmhFRA+mCToMMeGu0Jc0ovBWASrI8rFNzbpDL5ycnDBv3jwhkDCHvCLjA6xYsQKnTp3qkLOTn6RtkXxwDZYv/x4HU5vgM2I2XnltMZ4aFgjbPkDq3AqeWDL2USetUsrjZrKmTTuzCyv++xV2ni2C45CF+N27r2P2yABYkJC4I1LnSqV1t3Dsx6/wr4+/xI4jKShtuDdxBITHf+giw7ROx0Qpje9YCGlqXd73Hf67bDURAhKETliApa8+i0nRPgqQOn8sgaGZHTy8vWEhIcvT4juooVPovd7QPbGnyu+QXnQLuVjQZn9JSl1+HXug8HdjVT4uHd6Cr75cg0Mp9fAeQ7zkt17C1CHeD0TqXFh17nmi1hORWWOOoEGDERVgB0H2r7AmVT1sQXHyXnxJ9jEbDpKGTshTWPLqUsydGAVXEnx2JM64VVJiDVeQJ9aSGnKr7eSHIDoZ6rMaHE1QDV1zeA2aiNHhFqjPv4AbOeWok5uTPekVs3A5xB//V1WIPOVR7LT4WhcuTWXmRcvPaDloGDiGISrYBof3UqDn1GwUR3vDMXA4Rg+9gNT1CYjb+DmyLvwMcz2isG9nIT37NtSdRmDm3AnwJqoOpKakQRoTg0cFwDguC426Dgj0dSZKTwfGTqGICrJHQmoWikirwcs7AD5OFG9QqF8Neqa2cHVzguGBQ9i98iOUn3aDiV4jSgtvIz8zGfla9hhMu7zDQ3xEODs7Y/78+YJmzNatW3H48GEhXiNryYSQmt+DUn3+eWz+gaT1RAH6j12AF56bicG+dsSXJuQlOE1rr1b2oLIerXdNKKcTUfz2jdiTWAjHYc8R++VZjAiyIaEVGyCx2piCvtF4VhffwOmDV5Faow1zoniHeJnSiasQyafisP/IJZTrWCA6iMZKhXiwLu8MNnz7IxIIqUdOexYvLZqMSE/S9abJxOPUKgSTHwEKXGzqgICBsRi47yLi49fhy9WmWDQ5Cp62xgBteiknt2H1ziRU67ojPMgF5sSWEjYv+WL69L4Bxeln8OuObThyvQ4+Y57Ha6/MRoyPJY1RM2mutQr25NUa25pDBMn1kwdw/HIe9FzHITo6jJQfWADRn4nwTGMeDq/5FlvjM2E+6BksWboAYyPdYMrcAiZoWAW7A0Whpm0IMysr2Oo34FbKCcQfC8W4UFeYGWigubYMeTcTSaBPMX/VzcnW4n7fRv3Z467WrUTErgVdY0s4uDigkowxWAtFUVLTsUfY4GA4nDyDRtYjJ2MmXRsfjJo+F+X1Euw8cEbwoVLdpAVzW0faPZ/CiEmzSSdYphWhRj4qDOAdPQZhzheQZTMGEaQOZ6hDBk8SJ0QMGwi/c9nEyhmAsPAAOMlNPm0TZwwYNgnTb5YQX/sSdm0k60BNHWIbmcLWwRkj543DgsXD4MR8YEWNl3vGVqYcn5H9xBw/fhz79+8X+O9vvfUWvIlq6yzVlxDbJzkPlTV6qClKxaEtK3FKRlbQBNRkmYKhMUwtbODqHYiwYI+HUlKd1aXS56QyV3WnAGk3MlBY0wTrihwc3/E1Tm1v1UnnXV9CTpkMDYzIKpl4y4ERCPd1Ip8pNggdPhTBZ0gv+uRWfF6RhgOkDimtKUJmajLS8uvgFTMdU0eQbYIS1M66BhNiVxSTZhdpatXUW6D69mX8suEWDsvm9F0BJDs1M7W0h4dvIIL9XWFCGifOwcPx9DMpyFm5F7u+/hduJdFplLSA1OpKkXbhGM6kaSBk8myMiiAVStKtVmmiMSovzEZ6eg5KaROtLr6Og5u/xGGyNRGORdQvCVmKG9P8MzIiVlhYNCLI2MeAkFtTSSoOHzxDBn2GGEDU8ADyd6Mvg4dKO9GhsuYiYtNdR1FdI4zq8nH2l7VIjZetXiIkeH0bkD8bU8JNHv4IDvKBA1nCu4cSyzXmNL4/sB8r/nEHp30dYKJPiJ2s229nXiF2Uy1cB05EuJcZsYlVSFF06F5PfyoNsatJdGHlEYnpL0iRZzQQNp0qHuvCI3oG5i0gnmuoNx1raRDUNGEXMAxzX7aH/4DTOHMpg47k+nDxCUR4ZDgC3PmoJLdRqGvA2GsMXlpainyHsYhyN4WugBz14Bk9DfOLTUm/1gcxA11hLPedmqYRLbwxWPxbO/ifTiTefSZKpMQKcnWHt18Aacb4wcG061QUu+QdPXo0kpOTUVBQgF27dgmaMn/84x87NVbStnBHZGQA0uPO4FzcZpwloQ+5wCSETu4XSHGYfIsQ9U+TkXRtB46dD1sPd0LsPR1eFX5HY2hg7ghfUht1Jgdgl/evw9WjmmhuAHTIEyL3TZ29ANLJSlODBG+z34atnRUZjhnCKXQ8Zs4im4OtpMd/bi8uxJOHPV1T2Dm4InT0SEx/Zg4Ge5qokLpVIzN6T0TROOUevYCTezbiJJ06WtRojGictOjYrkFqJdp0QjOw8ETslIWwdSX1RfKKaEDjO2T6EjLH18X6HQlIPbkHCWSWrqZvCitbB0Q/NQmLX5iCUCeTu3r+KhwjOrsa27jDP9gHJzIv4NyetTQHNcjOhFRv9XRpjIg6pTHSFcbIAkNfIOUGJwvoM2InG5D8khZYesUgNiYMrqSQILciVdmJdnWpa1jCn04PvreO4dqJnWRlSjrszcTqIncmWmQcJiH32dqkpaWjb4nAYTOhTSrODsRCtXInK+Bnl6BG/UccPHcFcdsPo5SMszQNyLOjhTXcSJ4y68U5pHxB46Q0LNmu6X36Q3lNpklvbBuA0XMDHtJgNZi4DcOLbw8VeDdtggSySDR3CsQIvqY/pAiaUhIDN0x99Y/3ZdSzDcOMF0PJ3atiNSWJjhHsfaIxjS/igEqllK+HM9TCwgIxMTFkGXsQbI3Kvk22bduG0NBQgQ9/X+PogbZNJBa8/jpMnfchiY57jaQxRErfApVuRB7/JIRA6muriD9rAGdna9rQFJXSvWfMX+eL2Qd89U3SgIl9EMYvfIsEoftwJCkP6tSfxlopTKwtyUUzeTOkTayhvgplpU1wdbEUEAaDXmLoLCBDa49gnKST3LVbVdC28CA4hhFrKwBu9mSd2zeN7rRUHbtBWPLOW7B034tL+fXEWmwULBGNjIxhSBakrOlVX1uJWqkpuaC2ImvHu0Wp0zqwC8TE59+BX+RwnDx1GueJfSGxcUNgaBSxMAbAndV8VXb6kOsirVErzxhMXySBvvVBnEkpghq5tG1pVIeJlTkMdalfUupXXRXulDQLaqfatInxGGmauCN24kz4mQSQPIpYn3IEk1wNKr6llmnYY/QL76LZ3B0Hkm6DcDrFgSB5hzGdOoig0CRXHQ11NWTRDdh4sFfN1oHS0LWAZ9RTeN01ELFnEpHErhGyy6FnR0QeE5QDIxHgYgZtUvvk/vc2ybyrMo+9Def1ttAHfK88xP6ASu5/Rci0Lyd2J0hdYTt6OWrktQ2xsbECYufyi4uL8cMPP2Ds2LFgxH9fog3MPpBOGwGjhY3tvvd98KC+vl5w28uTigOA9FVSJzN1W+9YLKRrAclYyJldlzdOLUNbBMRMES5B4tjLcel1H9V0SWA/Aa8Gj28lElgboMsUgDq09CzhPXC8cC3q1re9bvkDC5Bom8AldBxeouvFboyRhok3Jj/fOYvxgZX26UsyULILw8xXQzFDINK6PufYWaGZfQBGTOOr7xrJQtMa8nnPibxi9l1FciX3FfkmV8WTfWtpSbxId3fiSZIPEEpVVVVC3FP5aEoKIdBlJKHw60f+YWv3enga6m+kLg9dGZHQm/HqzbfybVHyfa/GSMlt6X1xsrkm+9/7Eh/nEkTEroTRMzMzg42NTVtJfOy6efNm22/xRoSACAERAqqEgIjYlQBtZm/IH7FkeqtKKFopRQj+7clIqWM7lVK4WIgIARECXYYA89dVwWMXEXuXh6TzjMyOcXV1bcvAiJ0ip7T97u8b5vuXlZWBou6ADazEJEJAhED/QIBtXfpOgeFen/pJeHqvAU/iHQsrL1++/Mh1TbbhcJCQJz3JtBA4ytWT1N9ycoXNicdSUb9aDafaCylUQSF2Zz5xIBr5NsmsotntBY9Xb1NHxClfV1fLlg+W07G8rpbRn/lExN4H0OddmV36PiqJFwtvNnyKWL9+PT755JO2pjGCeJLThx9+CL6etMQInmU7HROfHDmilyzxXOxLTShZPd35zwZ88qxLDgLPKS4urs2nSnfK65jX09NTCIAje87wYB8tXU28ETAcZRuCo6Njt77nemTf9tf6EhF7V0f7AflYf102OR+Qrd9e8eLmic2TbMCAAViwYIHgU569U7IPC+bBFxUVtWsf90k1jsPaVSv+6CUEsrKy7ivhUaM4L1y40K6NsnnGtiBsxd3b1PFE0JPy5GEmf9+VsgwMDCg6midZwksE9iezalWdRMSuBIgzwpQdJ5VQXJ8VwRPU19cXv//974X2MrtCRlEwcpdPssUm/6yr93wy4I1BPmVnZ6sURp999hnOnTuHOXPmYNKkSfJNUXjPsEhJSWn3jlVXH7VxZfbLpk2bhI36ueeea9fex/XHLxRwPiMjA1FRUQgMDGzXDZYPpaent3v2qP/gdcbjlJqaKpyWOGqSqpOI2JUAcaZ25Sklpo7DwsKUULJyipCxYbg0NlLiOK19mXiz4OOrLPFvtsZVZWKWEyfeyNinz8MSI/COAu+Om93DylDFe0YWjNj5FPbBBx+ooso+r4NjGzBiHzVqFJYuXdquPiYweP4+bonnE7NAuf1MMMyePVvoAj9TBbEgIvZezhj2EcNsGPnJxzy96OjoXpasvM8ZsfIl4/spr2TFJXE9Hfm68jxVxV8p96lM+MXt0NPTU27h/Vgax9rlxDDujyN+X3RdNld4nJ6UPsngxCdBZnfKkmwtyn731X9R3bGXkL11iwMYtwp/uCi2QPXwoAhMfUwV97LZ4uciBEQIPMEQEBF7LweXEbs8D5CpDlWzHXrZBfFzEQIiBJ4wCIiIvZcDmpeX146/zoidNU8epVRZWSk4IeLju6rYMY9S/8W2iBB4VCDQUY7TV+0SEXsvIMsSexb6sFWnLLGq08CBA2U/H4n/zP+XyQBExP5IDInYiP9PIcDCVOaz93USEXsvIMyaMPJsGDbZ9/OjgNRyDsF6Ubz4qQgBEQIiBHoEAVErpkdga/2IETtT7LJkbm4u+GGX/X7w/2ZUUpiyGynXKPZrGvLKmqBn4QzfgED4eTnDso8CWz+4Tcp529Jcj8qiLCRfuYwryWkobjaDu5cvgsODKfKO4iATzXUUazLzBpJTSPXtViGqG7VgausMLwpB6OVqB2N9PVBAnH5Izai4nYHU5NZxyq8AjK1d4EsB2H09HGBhSFHnO7aqhcIElmTjSlIShUEshIGTM8yNzODk7Qc3Crau1ZexCDq25SG/mxtrUZZ/E1euUMzZm9koqNaGk4cvAoND4OtKMT8p8tV9/aMy68sykUQBKtLK9OAVHoUQd7O7sYUfUmEfvZY2ViE3LZlCVabgRkYeajVMYO/mK0RFc7Wj8HYcrLpdkqKJgr4U37qOK5ep7xm30ahvD08vf4QPCIC1geJ+tyviEf7RL0vlEYZHl5vGOs5MrbPwVJbYxHv48OGyn53/l9Yh79px7NmxCwePn8O1G1korGymYMg0sfwHYuSkaZg+KQYeFjoKF1XnBff/m+b6cty6dgw7t/yEuFOXCFnkoKzFCI4uHggaMh1Lnp+OcBcONyZbaFLUEZJIPLQHP+87hDOXbyInvwQ1TZowtnSAK2kY+QUEISx2Cp4a5gE92Weq6Kq0FrmXj2DnT7tw6GQSUtOyUVgFCgFI4xQQjXFTp2HK2IFwpbi6MuQnba5FSdYF/LJ5HTb/ehbJaSXQs7WDqZEpnPxH4JlFsxHrR5GxtGRxOVXREUV1kKO66iLcPHcQ27f9jKPnkilwfB6Ka7Vg6+QOn5BYzFr0LMZFULQkig0n659QEsHl1qU4bPpmNeJv2WH8YlO4OkfBXBa7V1F1ffisuTYfifu3YeuueCReTkVGTiHqNYxg7URRuAZPwIwZUxAb4gSjttilLagvz8e1U/ux/ac9OJZEfb9VjCZdijPs7ovoiQvx4oJRcDGh2MftOt6HnVBy0SJi7yFA2bKSDStkpvjMhvHy8qJwds4PKVGKyluJ2PbdF1i9+xKqtc1h5xEKd4qq3lhZiCxaMBtvV0LdwBxLpgbDVAkhyHgTYt4e65L3pRqmtLkGhWmnsXXlMny7JxlSKw94hw+BrqQBJZlXsfO7ZVC3doPtwmi4mJGXO4KUtLEMyUe24dsv1+N4Vj2FV3REQLgXhTRrRlVpPtLP7sGJoycwoMAOQ2LdCbGraqVJUZF9Chu/XoYffk1Bk7417L3C4amjhvqK28hI3Iu1JbXQNDLH/HF+MBaQWhOdwijo89ZvsOzbX5EncYSPH/WFmtxQnoEDG5ajsFEfpu/MQhjFPG3DMw+ZMX3xuoU24OxLB/DDsi+w+UQO9B3d4RXmhmBJM6pLb+H8nm9xu5r0yt9fgmhPC4opzIPVjLqaChTRxrVnx24cOn0VV2rq4ZacjTuNkYTY+2GzklbjxpENWPbvb3EsRwpLewcERhHMpfUozUvH4R1rUdGkA2OzWYj2MBGC1LfUleBG4j58t3wV9lwogqmbJ0KjfKHeVIlb1xPw3X+LYeblg6UjnGGo5A2Y16EqkojYewjla9euCSbDss+Zrz5mzBjZz87/Sytxdf9GbNpzHg1Wgyii/TOYOioMLuZaqMo7j+3frMCavYk4uC8BI2LpWGjV+1B2jNjZUIJNm/vSAKSx6jZST+3Dlr2X0OQ8Fq/97lVMjfGCuWY1kvf9By+/9S2O7D2JeRODYG9K/msI4dWXXMX+nftwMq0BbsPn4oXnZiLa1w4GGnXIvbgf33/xOb7+pRDFuSWobmGhk4oQu7QClyjY84Z9l6HuPBLz58/GxGEhcDRRR3n2Gfz45XKsP3QKhw5EYEiUN4IsNNBSV4r0Cwexacth5Kj7YNbS3+G5se7QpR2sMjMeX3zwT+zctQ57YyPhauFPx/3ej23nE+1Bb1pQXXwdJ/duxfbj2bAYMBuvvDwLIwZ4wEyrAQU3j2HF//4PVh/aioNTxsLfkYLFG6ihLOc8jhxKwLGj8Yg/noTMghpoGDShubGBCIcH1ddX74idUnYNW775AfFkShI+9VksmD0eg/wcoEfjl3psIz77bB2SEg4jgRQaQtwoXi2NRVXhDZyK24VfzxfCLnoB3nxzLmIDbKFRlYX4797D0o8OYl/cFTwzyF44WSnzkMhKDKoQnoqIvYdzjiMksf8TWWL++qBBg2Q/O//fXIobl9NQq+uGsXOfx6LZsXAzoyDC9IW5USjCQj2xP/4ySgsyUVhG/luUgNg7b4wy30hRX1mMTDrF3GqywLBpL2DR5HBaSNQzqQF8BxB/3UgbR/KKUFbbSMGhqW6KiVqRnYyLNwrQbB2GUVOnYuwgbxgI519D2BD1ZUc8eTXSImhpaqTNiT5STchIoLkEqUk3UW/gjWmLX8LCqQPgaNyKiE2NwhEe7Ib9CTdRkp+DogoaJwsJakqycOnkEZzNVYc/IZlXnxsLT+LVCokCKS+5kYCEv8Th8OELeCrGFRYGxgIFqcxR6FpZdLK4cxtZ2fnQcIrE/NffwMJRjmjlpEhhGDoCQ8Ktse5sJrJpQ62tJ6ytr47C5EPYunEbEjOroWvhCHc1TRSU0vBSpSpQ9Li/a1RpQ2EKLtyohnXIXLzy6nMY5mMJPaEjZgiJiKBNaS/OJRYjN7cU1TRMhnQSrCjKpghnGWg08cTEZxdjarSLcKpq0XFGaJgvDLT2oqSgCFVEEHHfHsckIvYejhqbdsv8YbNvGGtra8Gj20OLk5jAe9BIzKCAFyNGMuXaitSb6ytxO/0izifdQH6NDpVHEdUN++Fo+9AOPCCDhMz3TSmIs48hBoW7wUBgmxBSbihFCgvaKhphGWYDc31tSO6SQfW1lahrIvmCmTkszI2hI2NqShtQXpKHW7n5qKcFLJU2ornlAXUr+5W6CXyGjMEsH19MHuoNKyNG6kQh1lUi/+YFJF5KRxGxVTytbGBKSA/SJpQXZ5OQNU0Qwg0ZPxRuMqTObVPTR8CQoXA3PoirF64gs2gMfO2MBWpe2U1/eHkSGJg5I2zEdEgH+GHqILtWpE5wbqJTR05KPI6cK0SLFrEJrYyhzTwjNQ2Yuw/EpDkmGKJuRSwmQ1wnltOqH1Opun5Cf+y6wsyHZFIzgOhZiHChkwUjdWIZ1RAP/crZM7iWcwcSYwdaTzS3hDknhbqWHkytneGj5ocwb5u7fW9CbTmxoM5cIcLDAK6O1jDoRHD8cPj2fw4RsfdgDNiRT0lJCWRBD5haZ2dTXUpqJoic/Q4i5TO3VOPW5UP48fuVWLPnLKrMBmHqiKHwsXqchoeixVt5Y8yzf4bXqFrY+VoLlDYjiozE7Vi2/Cdkq9njmSlD4MGaMXf7r29iBRN9LdSW5NIJKA+l1dagvY4Eqhm4cj4RF64WoR7s64WRuzzQ+vhe3QwxC/6EGPlqaJyykn7FhlUrsf7Xi2iyH4moodHwJDYMMVtIJlCIgtwG6Jl4INjbtgM1rgZ9Z28EmOkhMS8HBcU1qGuWEmJXEWtJvh/UMiO7IEx4lq6251JiqZTjRsKPWLZsBX48WgjrYW9hZKQLTPVaR8vcYxhm08WppT4NRbtbn0ulLa0nMOGNKv8QYreMwG8+imhXaWNlNk7sXIOVK9cj4XoTgqcNRAwRGkYC0aAJa6+hWPg7L4yr1oW7G022liaSK5AA/5cf8MXas1B3isb0CWGw0NEU5EDtCu/BD7YdYfsWmbdQkRXTAyCq4hMWmnbUhvH39+9x1c012Ti2fSNJ9U/gZrkhuSTwR5CvPbQFTNYfC79nXVGT6MLExg0hHNebFntDdSFuntmBT9//BDtT1TBo/m/xAgmErdpUBNVg7BKIQQHOOLeDNEl+3ABTSQVC7ICsc/uxbfNunM2sgIYOuz1Vh9pdKr9nrev9V83VGYjftBbb9p5FZpUpoob4w9/TBloCL6IR9dUVqCpvhAZT8czM7ZAkusbEbtOFem45qqrv8qVlO1yHvKr/2UystFT8/PlybDqchrIGK4yNZvaTrsCmUNSee/vsvTtF+VT7TIqyG4ew+tutOHQ+E3CIhZe/D5wtddqaIdE2hq0rXfRE2tJAqrkZOLP3WwpAsxaX6+zw9J/ew6xIa1L1vH8M2wrpxg17VHV3d8elS6QsQQ7BRMTeDeCpMivrrsv7G7ewsLjPj3R32qOuY43AoWMwIqsYtccv4/rp7Vi5wgKWf3oRg10MlEI1dKc9vc7L2hMVebgcvw4ff7Ac+zPVETPvA3z8h5nwtdZrhygkRv6YMG8WknNW4Keja/CHuK/RSCxdiZYODEyMYO7qgMZS8kyprgk6GfdrUtOxQejI8RiRX476U8m4cnQzVlkQC+l3CxHpwBswswHoIgqQiHEFSQINIhDV1Fr6i3mhoE2yR+rQ0nfGoBnTMbZ6O+Iv5eLnL/9GxnameGtWBAmN76l0tn4h7GaPYD+Ij+4QiglTR6KsvhHnb57H7nXfwdLcFC/NjIRVKz9G6ALbW5TnJ+Pw5i/wybKfcLPRFdPf+Rc+fCGCBP5ESMhA8xj+V86W9Bh2XJlNZlZMQEBAF4skPmYDmfg3sACxdfWraZghaMxz+PuqTVj/5f9iip8E107uxJa4a6gVpIxdLPpRyMb8TTrWHt/6b/z2rX8iLksPE1/7El99tABBHZC60Fzi3doPmIM/fPIp/kEb2eQh4QTLcIycuRQffvof/O03T8FdXwMSbV0yUFLlUmshAxYKKdjQ1DZO6pqWCJ/8Cv65egvW/ve3GOXagAtHf8aOI6moI6muHssJbLXQQKyAguL7g5k3197B7cIatEhMYWigTb7x+2/ApC2kKSXMQzJxF5qhTicjGwxZ9Fes30NC0k8WwEfrJn5aswvns0pQp0C+cW/vUuW4dIAZbaL1xBptbCJWXeuEgg4J4uf+9j/YuGM9/v7KcBgVncL+n/chMb2qbSOSttShNCsRP33xIf7w8TZkaobihY++xqevDYXlY47UGQwiYu8wT/r6Z0tdGrZ89Abe+ccmnEorhfzyl+hYwG/QCIwdEgrrumrkXMtGqYIF1ddt7Hn5bE17Db+s+gve/P1qXG7wxuK//4AV702ECwkfO2Unk3aFpUcMZr/+CTb8cgxnE49h1/cfYcmkAbCmE3QTRaQxMKHYncSrVFVqqbuB9e+/jLc/3Y6LxDpplKtYQ9cKIXTCGj3QH2ZV5ci5noc7LbqkK+0AJxdD1N1Jw6lLWSAlDLlE9gs3LuNcCWmU2DiTUFLvnqBYLpdKbsnAKD/5IFZ9+Fv8z/8dQH69/CRTg0TXGjFzF2IiCSNrs64jK78StYQ4FSV+qkY8sk7HVtFHynpGRET5tR/xxoIX8SXZGtypkde5VIehbSjGTByDYA9zlJIgPrPgTitiJwPBgpTD+P4f7+HPK4+i2mEc/vD5V/jz/PC79gjKamD/lSMidhXDvqWOdL3PnMDO79cj7nQaSmrkF5UUVcU0AXMJUWhqwYgk+awD/XgkKapJ9ezg2k/x589+RanVULy77Bt8+FwkGVl17Vjb6n2SkAQhcsFZGVFjAlVJh2ItfULsKgRES00BWSaewPZVa3DwfC5pSsiPUwu5GchGRsFtVOhok4WsIWlcqMPYyhkBwaEwrSvA8e1E6RbJtgNCf813SG98L9LKW+A+MIisVQ2h3W9j20Aqf+k4d2g/9pCF7OEU4vu2gy1tQhlXkUwGWM16FjAy1LqfDUanTT5wEpOMvlTdhtu+mS2ozE3GscN7sOqH/bheXNVuA0ZLFW6lk0uLkkro6RqQ3EOXWtqE28mHsf6/n+Dz7TdgEbEAn6z4J14cSUHA+5nV165vvfzRb1Orl+1+bD/XMPTFoKGeMGq5gh1rVmPL7mNIIX3iArKSSzq8EZ9/+hk27E+Bvr0/hkT7waRfSKEegLeZKNerR7Fr8wmUGYfg+fc+wAtj3KFDdGsDGWU0CKynbpbb3BoWrUaqDm097Xa8+a6UxAZZ3YlOL1+mhlEABg8nFwa157Bp1bfYHncaN24V0DilIfHAWvznH/9HMoFMmLoEITrCWxgnLRMH+EePwOgQfaSfXIOPPlmHsxmlqCnLQsL6f+Lj786gXC8c40dFwMFUr8fHZd70ehUVSs0QVo5+CA61Q0VWAr7+7EvsO5OKvMJiFOak4uTuFXjnzX/gUE4DQkYPQbCTGSG9DsibQr9JiU0opbFRJ4pdpr4qD8Pu3PNYdTvKlpoElqGxGO5uhLyE7/HFNztw9PxN5BfeplPUOexa9QnxznchqcQMvqGRCHQzRUtNLi4nxGHPwQwY+k3C2396A5OCLaAmzDUWaLP3xe60vHt5a2pqhODx3fuq+7n7kcvX/cY+EV+QHvvA6YsxhajA9cd/wkdv7sZ/tDVocbARTj1q69Rh7jGEfIosxqRwq351rNRdeEsFCrsaRTlnsfKd6dj4XnsSSE2H/HdYWsPK3hsjZy/CtFhf2Bi16vErqquFFllNTR2qm0itTU+n27AQqH5FBXflmYYpYmY9jynn/orNZzfg/fNb8TF5IVMjGrW5sQ41dRLY+o/GnIXzMDrYslW1UV0fdt5DMGfJXKT9bSUOrf4jzm/7G7lHIEMa0te/U2uGyW8uxeQIRxj3gjxsPdl0QLRd6VNbHnVSd/TB0CnTcfbS59i969948dAKkmGw46sWOiXVknaPFJ6jl+K1xSPhaW1wH+wFFUdG7rQ9qUto/rYf6raaunrToz7RhqJtEYVnX5uGS+9vwP5v/ojDa4gAoE1ISmyahtpqNGnbIWryPMx/egQ8TejMR8KC5uYGNNaWI/PiNvzvgjj8TU52w+3Q0SdZibUVbN0GYPbzz2NEoA0ZLfWOBpbNRVXEO2WYi4i9qzNPLh/7g2GDJFniXb62thYc6/ThiRaVyzC89CddePz6Kw4eOYHEpHRUEhXl4B2BiKjBGDZ8KKJDvWCtr0rmw8Nb/sAcEkPY+w/HrCU3Ubz6Z5xOr0RlowQNzRqwsDKHgeBIio74RZm4nVcBu8gJGEOm+A9KEh1D2Dl7ICKoirxD2nXbTww7ZeOrZ0kdJu5j8MZf9eGz91ccSjiFcxczUKtpDmf/QYiIHoJhw2IRFewOSz0ZViOWkaENgkYuxHvEh9+89WfEH0tCfrMFvCKGInbMDMycMhjuFnp3rTx71jJWn3MiA7feJA0dc3gNehrv/J00snb/ivgT53AlNRtNxm7kayUckdHDyFPpUAR5kKGOAn8papomcCDPmyGDDGDt4wBjYrf1JrECgqmpafeLUDdE4KQ38YmhN/b8cgjHz5zH1exqGNq4YkBsBAYPHYGhgyPh72IBbR4mcvQVOHQq5mYUoGHncdworkCzNslx1AxgaUGsT0bgJFgtyUlG9m11RE6ejQaWL5A20+OURMTeg9FiZ18ODg5tX3KEInYv4O39YEQl+0Bd0wAOfjGYbu2FmPFzyJFYGQlRtWFgag5LK0tYmBpDv6NHPdnHj+x/sma09MSw2W/BJXI68ssaIaGF1NwigZ4+6ULzUZ5025vJNUB9owas3LxgRwLVB9Gd6vo2CB67CH8JLoeunZvgW6Y73ecgyYwEe5rUtQzh6D8Us2z8MHTSbRQVfyMPLAAAB6NJREFUV6JRXQdGpha0WdFlagQ9Om216wNp+eiZOCFk+Gyi3mPwdH4RqqVk6WhuARs7e3LHTCePXrLXBKpS555edo/6R2wMHSNr+A6cCBv3cIybXYyS0nI065iC1XetrKyof/pCW9v1725l6poWCKKxeWdAPbRMbWEiR/X2pD08VrKg1t37Xg3axo4IHz0LToFDMaOoGMUVtJr0jWEm9MOSDOBo/snaR+Nn7RGFp1+zx4CpJMuqkUJDQiwlNW3iw5M3Rx4bovabyP9NvdQQ7uR3xlBHtnF3r2X9mbvns74/W93PdTN/U0a13759G5mZmdizZ0+XETs3X11CHues6EhOl1c/90dZ1atLtGFo6YJAvpRQqBrByIR8n5vcOxwpodTuFaGuQUZX1k7C1bVtm8onFoGWnikcPPjqXn2qzU0qjtpEqdp7CFe36iZNJvZLb9yPY3OvvcSq0zWFnStf954qviOtH+6zk69wKc6j3KcSonDs7e0FAyXlltx5ab07P3Ve7hP/hsPfBQUFCf1k5H7s2LF2IfKeeACIHRQhIEKgSxDgE1ZfustW1AgRsSuCSheehYSEICoqSuALspnwlStXsGXLli58KWYRISBCQIRA30JAROw9hK+xsTEiIyOF4BpcBLsY2LRpExITE3tYoviZCAERAiIElAMBEbH3Ao5hYWGkGTFMoNrZcxs7+fniiy+QlpbWi1LFT0UIiBAQIdA7CIjC017Az87ODqNGjcKJEyeQkJCA4uJi7Nu3T+CnvfLKK1135duLNnTlU1bDZLehbBzBsoCcnJyufPZY52FHbayttHv37nYBUR7rTlHjORQj60Kzd9GPPvrovu6weqe8JhDfs/DuUUqsdSPfptLSUnBkoZSUFBw9erTXTeUwlfKGaaxtI19fVyrgE7lM95z542wN3dPE3hxl+usy1709Laur34mIvauQ6iQfU+3Tpk0TAlvn5uaCBakbNmwQ9NpnzZqF0aNHd/Kl6h6zVR9r8pSVleHAgQNgf/Kse8/h8njC8cTjhSWfGhoahOfyzzre88Tv7oLpWEZf/962bRv4etISb1zvv/++0C15i03WB5dXG2TELo/ouwKH3iCxrpTPqpTybWI2Js+3/fv3IykpqStF3JdHvs0c/lFHTh20J6qUDEdZYv16+fbKnnf2n9cEE1KcuF0cu4FP8bzOmPjjUJV9nUTE3ksIM4U0fvx4CrV1E5s3bxYGjgdy/fr1gkCVEf2ECRMEdo2MAuhlld3+nJE2Lxz+z5QMUyN8z0ZVrSbU99tQc/6HJZ7A8gvqYfkflffcbkUbEveFqT1FiRe2om8U5ZU96w4ykH3DG62MupM9e9h/3qjlE2/YnB6EQPhdx81cVkZ3+yn7rqv/5V1ey3/DcQ744nHo7rzq6zbLt/Nh97yRyCh+3nT5xMzKFYzYVdVOEbE/bJS68N6HLPBeeuklIaISU8SMzBlpnjp1ChcuXMBf//pXQcedg13LUxJdKFopWRh586bCCCMvL0+4lFEwl/s4Jka4ihAHw4ipSUWJTz3dQdS8gPmb7iZG0l3ZVOXLzcoiT5KdUIEPes4nuEcxMfHRH+tEmbCQwZbnFM8bmbqjiwvFVyXE39dJROxKgjDrtH/44YeCq4FDhw4Jxy/mZTNV9O677woGCmfPnoWtLcdtUW0KDg4m8/CxAn9WFs6vYwuYmugMCXAfuktFcn7m6XcnMULr7mbBPEtFifvCfeKrY+I6OqtH1GrqCK17vxlBKTp1MqKS52nf+6LzO/5GVhZvZjxeXAbXwZtidzbRzmvp+ZvO5kdna4Rr6oxY4E2K+8jIfRgpW/Rkw+9uT0TE3l2IPSC/m5sb/v3vfwu87I0byVPj55+35Wad9675kmn7RGk3M2bMAF8PSowAKyoqFGZJT08XQnopfNnJQz6xXLx4sZO3ih+zQLCgoEDxy06ectsUIW9mR/Cl6F0nRYmPHwIBGeLtmI3ZDiwQ7U5iAkcmG2D+Mwu62U0Hl8M8bXked3fKVVZeDlavaO7I2Jcd6+HNSNYf+XdM4PC6YlYtl8kyN1XgARGxy4+Cku6ZT8taMXw9LompJ16gilJoaKiixw999igIjh/aSDGDCIEnEAI91+F5AoEhdkmEgAgBEQJPAgRExP4kjKLYBxECIgRECMhBQETscsAQb0UIiBAQIfAkQEBE7E/CKIp9ECEgQkCEgBwERMQuBwzxVoSACAERAk8CBETE/iSMotgHEQIiBEQIyEFAROxywBBvRQiIEBAh8CRAQETsT8Ioin0QISBCQISAHARExC4HDPFWhIAIARECTwIERMT+JIyi2AcRAiIERAjIQaCdS4HU1NS2Vy+//DIcHR3bfos3IgRECIgQECHQ/xCQD5TDOJu9xnZM7RA7u3SVpbi4ONmt+F+EgAgBEQIiBB5BCMjjbPnmtUPsHOpNltjTWn97WJO1RfwvQkCEgAgBEQKtEOBAPuwJlZM8zm592/pXjVxT3u+wWj6HeC9CQISACAERAo8VBETh6WM1XGJjRQiIEBAh8HAIiIj94TASc4gQECEgQuCxgoCI2B+r4RIbK0JAhIAIgYdDQETsD4eRmEOEgAgBEQKPFQT+Hz8rrh83u3ayAAAAAElFTkSuQmCC"
- }
- },
- "cell_type": "markdown",
- "id": "edb16fc5",
- "metadata": {},
- "source": [
- "But what happens with 2D arrays (or multidimensional arrays)? \n",
- ""
- ]
- },
- {
- "attachments": {
- "rowcol.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAADrCAYAAACSPxQ3AAABPmlDQ1BJQ0MgUHJvZmlsZQAAKJFjYGDiSSwoyGFhYGDIzSspCnJ3UoiIjFJgf8bAxMDPwAnEMonJxQWOAQE+QCUMMBoVfLvGwAiiL+uCzLp9qneX98mX6xNmXItjMGSOxVSPArhSUouTgfQfII5PLigqYWBgjAGylctLCkDsBiBbpAjoKCB7CoidDmGvALGTIOw9YDUhQc5A9gUgWyA5IzEFyH4AZOskIYmnI7Gh9oIAq5G5kyEBd5IMSlIrSkC0c35BZVFmekaJgiMwdFIVPPOS9XQUjAyMjBgYQGENUf1ZDByGjGKnEGJFqxgYrOsZGJi+IcSinzEwrLnBwCC4HyGm4cbAIA4Mj33lBYlFiXAHMH5jKU4zNoKweYqA3vzx//9nWQYG9l0MDH+L/v//Pff//79LGBiYbzIwHCgEAGmsXtKRMhyuAAAAYmVYSWZNTQAqAAAACAACARIAAwAAAAEAAQAAh2kABAAAAAEAAAAmAAAAAAADkoYABwAAABIAAABQoAIABAAAAAEAAAHyoAMABAAAAAEAAADrAAAAAEFTQ0lJAAAAU2NyZWVuc2hvdII/jnAAAAI9aVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA2LjAuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvIgogICAgICAgICAgICB4bWxuczp0aWZmPSJodHRwOi8vbnMuYWRvYmUuY29tL3RpZmYvMS4wLyI+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj4yMzU8L2V4aWY6UGl4ZWxZRGltZW5zaW9uPgogICAgICAgICA8ZXhpZjpVc2VyQ29tbWVudD5TY3JlZW5zaG90PC9leGlmOlVzZXJDb21tZW50PgogICAgICAgICA8ZXhpZjpQaXhlbFhEaW1lbnNpb24+NDk4PC9leGlmOlBpeGVsWERpbWVuc2lvbj4KICAgICAgICAgPHRpZmY6T3JpZW50YXRpb24+MTwvdGlmZjpPcmllbnRhdGlvbj4KICAgICAgPC9yZGY6RGVzY3JpcHRpb24+CiAgIDwvcmRmOlJERj4KPC94OnhtcG1ldGE+CmIGGowAAEAASURBVHgB7F0HXFTH1v/vsssuLB2RDtKkiA0b9hJ7L7EkpptukpfkJXkv+dJfXmISY0s0akyiJsYeey/YoqhYUBSULihFemeX3f3OWVhdEJAFoui7429ly9yZc/8z97Q5c0akpQKhCAgICAgICAgICAgIPJAIiB9IqgWiBQQEBAQEBAQEBAQEdAgIglyYCAICAgICAgICAgIPMAKCIH+AB08gXUBAQEBAQEBAQEAQ5MIcEBAQEBAQEBAQEHiAERAE+QM8eALpAgICAgICAgICAoIgF+aAgICAgICAgICAwAOMgCDIH+DBE0gXEBAQEBAQEBAQEAS5MAcEBAQEBAQEBAQEHmAEJHrabWxskJ+fr/sYEhKi/1r4KyAgICAgICAgICAg8DcjcPbsWV0P1tbWyMvLM6o3kT6zm0gkMupCobKAgICAgICAgICAgEDzI2BswtVbFrmZmRlKS0t1FD399NPNT5nQooCAgICAgICAgICAQK0IrFixQvc9y2Jjyy1BPm7cOKxZswahoaFYvny5se0I9QUEBAQEBAQEBAQEBBqJwJUrVxAeHg6WxcYWIdjNWMSE+gICAgICAgICAgItCAFBkLegwRBIERAQEBAQEBAQEDAWAUGQG4uYUF9AQEBAQEBAQECgBSEgCPIWNBgCKQICAgICAgICAgLGIiAIcmMRE+oLCAgICAgICAgItCAEBEHeggZDIEVAQEBAQEBAQEDAWAQEQW4sYkJ9AQEBAQEBAQEBgRaEwK195E2mSauBSqVERYUaarUGWmqQs8WJTUwgFoshMZHCxERM3zW5pyY1oFaVoUyphVQmh6mkPmLofsrLodKaQC4zhbi+qrVRpFWjvKwckMggk5rUVkP4TkBAQEBAQEBAQKDJCDSTRa5BQXoUVv7nZYwbPgDdQjqiXbsO6NpzAEaOfwwvv/kh5i/fhIirqSgoq9AJ+SZT3qgG1Liw8V0MHTAWX/xxCjml6jpa0aA4/TyW/Gs6xj83D+cyi+uoV/fXyoxw/GfGY3h/VSQq6q4m/CIgICAgICAgICDQJASaxSLXqsuQdmk/Vv2yDedVFnBoZQFLU6JLU4rMazG4Hn8B+zf9hiUePfHcPz/AS+NDYCu7H1aqFmlXIhB+5hzi/vMhFBbf4eVRwbCWGeozGpTkXMXGH2Zhzh8Hcc1Uimu5SoQ4KmCMUa6FGGbWDpArmgXiJg2ycLGAgICAgICAwMOLQPNIGa0WGrUKFRIbdB/5Eb7/bio85CSo6buSonzcvJGIc0e2YMnS1Vjw1VwEtv8B44LsqqFamSRedIfrXVmSi5xCDaxsrWFmKrklTLm+4UEvalUpCgoKoZVawNrSHCa1Sl0RLKztYSFSoSDzLH76+hvYWX2Mx/r7wkJaKcxVhddxaNVCfL/6KNKzCwFnCS0LVCO1QR9kTj3xwaJQXl+4RfPtC7Ug8qvRf/s34Z2AgICAgICAgIBAwxFoHkHOC9+iqvVvEznMzeWQ6dafTSEzU8DWwQW+gZ5QJkXg7V9O4dzVAowlQS4iJ3tFWQGSrlzApSvJyFfK4ODiBm9fX3g428FMqkLiiQ1Yvi8b/R9/GoOCnWEq1iIv6RTCwjPRplc/dPSwJtu3AtlJp/HnhgNQew3F5HE90drM0MrWAyKCuaUNZHJLOPoHwjL3OJbMXUjC/B2M6uIOU3U+osLW4ceVB1Bo5YQ2rVW4ZiKhNf7qWgErDdk3khCfREsFSlO0dnWHm6sTtXNbgdCq8nH17DncVPijB9EtJRK0mgrkZcThUmQ0ktMLIbNzhJunN3y93GFnKdetwyvzU3H+QiKkDs6Ql2Xh+o10FKgsEdC1OwJcLelehSIgICAgICAgICBwG4HmEeTUnogEOS9+q1RqaKra16groCwvRn7OTVyLPoajURkQ2bSBh6O5roZamYczO3/G/MVrcfTcFWSVmcLF0w+dew/FlGlTMTTUBRmxJ7F13VHcdOqO7r6tYSfLR9iyT/DG0lj0fnkBvv9oJFqhEPFnDmD18g1wGO2NYSNCSZDfvknDdxKJKUxk5mg//lWMVe/C3FU7sWhhK9i89yx8VaexcvlGxCo9MPXFUcheswirU3VG9a0mKspzEHVkG/5YvQlHImKQXS6Hu1879Bw0GlMeHYF27jZgHaYi9xJ+/eJ9nHR6BWsXP4nWYjWyEv7Cyh8W4I+dJxF/LRemrVzgE9QVw8ZNw9QJg9DW2QJZl7fhvx+sRLGdGxTFqbgSl4QCiS9e/nYZ3h/vb3zQ3S3KhTcCAgICAgICAg8jAs0nyCky3URditSLu/Dj1/GQlJVBqVRR5DYJ8uxMJF2NQUqRBYZOfx4Dg6x17ubMSzsw77slOJ7riF5jpqOVXI38jERcPLwW8zLLILOaiXZkOTsq9uNCxEXcfCIUioIIbNoaies5+Qjfvgnnnh2IAbY5SLwSh7QKK3Rq4wk7Rd12q0QqYT8ApJZeGDl2JnKzcvHT7jX4fnYe2uAq9kWXoseUmZg63B2rt7Arn93gHINPS/4VpYg7vg7ffrUIJ9NkCOoYimBFBVKjL2D9L5kkmD3hPq0n7ExF0JCSkpJ0HVczE5Cr0cKmJAV7fv0OSzdcgEPH/pg2xAba0hwkXL6INUvSUS4xx+uP90NhVgpZ+rGI/isG/qG90WNIJ9i3boMuPrZ1LBc8jNNSuCcBAQEBAQEBgYYi0CyCvNKzLoaYgtuSIrdi0dUKlBSXQmUQri229sWUV97Bv14ZBU8rGVnvBQjftBJHk6UY995n+PdTveFkpkHO9UisXzQbi3fsw55DvRE8thM6uVlh3flwRF2fAiTuwbGkLFgqFMhPO4GDJ5PQOTQPCYmJ0Ng4ws/fDZb1bCsTiSsXvDVaMWxcO+LRGS8j4+bXWLfndxzXWqJtn2l4/NHB8HK4DhOdulG5ns3uhsKUv7CUFY8Me0x54z08N7YHXCxKcGLtd/h0zi7EXI5HbnF3EuSkAEhlUEjEKC0oQblai9yEI1i9+QzkHZ7AR1+/hX5t7UiQZ+PCgd8xa/Zy7N+5D/16tYMnjZwJ/XPvOhL//uJfGN3NB1Zm5EWgtqo7+Bs6xEI9AQEBAQEBAYGHGYFmEeTkfKYlctozTnum3YJ6YNSoznCyMCMXswalhdlIjDqJQ6dTkZqSBSX731kiqVIREXYVWrvBdP5qL7jbyHU4O3qFYAhtYdt/7BKuXo5BzoRJ6N3NA+sjz+LIyZPIOnUEGVoXDBvdDZcPHsPxPYcx3NkSCQnZsHPuAX9PR916dF2DZhh6JpLI4RLQD088n4GMzEWIKPLBlCceRWhbB5iqbujuiQW4zh7XliBiyxL8GZGDHi9+hJnTB8PDile+LeHp7QZ7KyVyaAmhsEQF2NK6uqkcZiR8leUltG9dTVH9pxGdLUP/l8ahb5ATdEv4ps7oPGAoBuzdj4WHohGTcBPOIlIfRBJ49x2DMb0D7lN0f13oCd8LCAgICAgICLQ0BJpJkLNsJovRxAzObYfhxbeehI+FjFzBlFSFXOtZqefx2zefYPGBP7Dp6BAETWoPMxSjMF9F15hDIWeBWFVEUgpIs4QZbU/LpoQqatiic5+ecF55Fnt/W4CI1ATIXcbjydcmYDcFz+0+tQW7Xdvi6g0RHDsEw8u5cv1d31zNv1pN1Qp+VTS52NQKbUPH490v/ZChtEJAh0BY0XY0japGBL36Oo7vikSJZQgmTHoE7johzq1TwhhzC6JXgvySYhLaKhL8ZmSRm0JOghyaMpRXkDJQUoRyjQlkCnNIDUxrqUwBa/pOpKwU+DCr/NFELgN56IUiICAgICAgICAgUC8CdS8m13vZnT/yVjCWOyYUTGZOgsmMsqGZklWqsLKHZ2AfTJkynHZyZWD3zuNILyWrVewIDz8LlGadwqkL6SDvs65oym7iSuQFJGZo4eLmATtrS7h27I2eHpZIv3ga51Nz4U1WbGi7EAwcFIDS1FP447fNSNBawZeEsGM96+PcgVqtZv8BbSm7fetSc3sEdOuL/r07wonc/jr5eUuI6m34cpQR3RKZFWytSVBXkksGu4q+p4x2Kg3UFRVQ03o4FzHhoBPkWiUFAIph7+wOKxQhJvwMxQroE9FQAFziJURQxL7W0QkeLjaQ0xo+Y6nPjqfvRvgrICAgICAgICAgUBsCt6VZbb8a8x0vlFOhHeW6PdLVLhXJ4Nm1H/p6WeNa+DFcSi8lie+CvqP7wrIkFsv++wV+2XYU584dx5+/zMXspVuRbh6AXn06w8VaAlmr9hgwwAsScsyXqO3Rs18XOChs0bHvAPjIy8llnwsLB2906+QLRe0byG+Ro6ZIepHIFFLaHH5LGNOvOkWk6h50lSnAjbLOUuEUs1TTxBOdQj2gyjiOFb9sQGRiJgXKpeLUzhX45rsVOHo5Bxregqe7mNqT0P5z/qCh/fUktx07DsTAtjJc2rsQX8/7A0dOn8XxvWswZ9YC7DhTiPY9+6GTjyNkHP0PFSkEemFf1aDwR0BAQEBAQEBAQKAWBJrPtU5CsFIrqFpTrtGZzD4Y/fp6YNXCEzh2PgOj2tqg/Zg38ErYRXy17ne898wGXeIVNeVrl9r7Y8prz2F83wAKGGNpaIuu/frCcelp5Jq2R2gnV0hoPd4xoBd6dW6NU8cr4Nq2LzpTANndNBMN5UDXUC2JodCuQavuIwl8FUtysQRSThYjssSgGW9jzIm3sXb+TOxbzPnXtZTzRoXS0iKU0tY5LxK+6qoId3bhVzkZdM0pHLvhuTefxLl//ohV372BjQsIeqqv0pghaOBTeP7JEfBzMEMaRf+L6Uq27A2vr41E4TsBAQEBAQEBAQGB5hHkYimsXQPRb0R/5LcLpKjtWsSpiQ26DRuJDjulcLShqHUq5iTcZ5I169VhMX7ZsB+xuRboOngsHn9iMgaGeMOS1skrLVwxnLuMxLQBB3HeeyaG+XNgnAhWrYMwevIkXFLFYvCjj8CLrPf6iwiuwQMwaogcgzq63rKea7tGZOaEjr07o49vd3hSvll2sNu3HY1567wx+PefsHxjGFJK7RDSZyAGdXdB3KkIKN2D4GRT6XZXK8tRUsGKgDkdukJKjtQSnce8h2X2vvhp6W/YfyYJCq+eGDdlOqaM6UNR8hYUU6CFrUcH9AodANsu3pT8phYcayNW+E5AQEBAQEBA4H8WARHtkdYZfo899hjWrFmD0NBQnDhx4m8ChCxNOhmNT0TTu6ANO2JK7mYoG9bXv9fdAl1YW5v6Ovf6rzJtH14d9Tw2lk/F4YhZ6FAz0xy77lsYzfcaI6E/AQEBAQEBAYFKBHr27Inw8HBMmzYNq1evNgqWe2zyiego09qFOFPdGCFeeV1LEuIalBWk4fzhIzibVQr3jn5wrC38XBDiRk1UobKAgICAgICAQO0I3GNBXjsRD9W32mKcWf8VZn64Eplib4yhPfIOdwnAe6juX7gZAQEBAQEBAYF7isDdFpUbRIyKAr6io6ORkpLSoPoPdSVtGWKvpEHs0BZD+45Ae1kCdu1IatAtKyhbnYSi3e9F4eUIft0RrX8vOhf6eKARYK+atbW10ffAc+1eFJ3Xr46+9PO+graKcj1+ceHP97MwXRoKkOXtsaamfAb0/S+GWDFfEtcSs1Pbd3ej3MbG5m5Vqv3OmCiVSjB/NKbox9aYa+q6z/ra4H4YB6lUWitG9V3bXL81i9S4efMm3nvvPezZs6e56Hoo2jkVvh+/GnEnTk6U8c2sjtNejGjnblX1Dyg/IDwBGzPh79aH/nfuy9jSmGuM7UOo33gEZDLK4OjmZnQDjZlnjRH+TF9d1/HcYqFdWlqqE5hyeWVGyTI6G+J+zjsW4kwXG0XGCiyjB6KBFzAeeiHKykVNI4MxZuFlbPH29m7wJYwLY1JQUAAXF5c6x7W2Bnm+1TUPaqvP35mbU8IuI++JcWF8+NrWrVujc+fOuuejMUpOXXTd7fsmC3Ie7KysLEqRmnC3vlrE71ZWVkbTUR9juFtjei2bJ1TNB6HmtVy3uLi45tfN/pnHjPvil16bvFsnjIGdXfUz5O92Df9u7GRmmvihZRyYyTaUqekZckNo0tdh5t3Qwky2sLBQxxh4Dhl7Xw3tR1+PaWMrpCGFx5PrMsNjJmSMwOTrcnNzG9JNtTpXr16t9vlB/2Bra2v0mLKQY+yNKaxANHRc9e0y3zBmTPk6CwsLGGv58r0Yeib4WeR5yPfJQqomDVxf8MLqR6nyr7OzM2bNmoWpU6eCeea9Kk0W5EwoD7heSPn4+GD06NH3in6Ul5cjMjISly5dQocOHdClS5d6+26MILeklLHGanZ6IpKTk3W7Adq0aaMbXP339/Nvfj4dBRsWhvT0dAwdOhQN0ZAZN3d3d6PIZsyMFXgsjPbv348tW7bodlBMmjSpQX3yGBlbioqKGsyIU1NTsWLFCt39zJw5E42ZR8bQx8oMM/2GFFYweDwvX76MAQMGoFOnTg25TFeHFabs7OwG1zemImO2adMm3bwZP368MZf+bXUZK96Vk5GRgT59aNunl5euL3t7+1s8rKGds0Bm3mdMqUuQX7t2TTfnfX19MWLEiGpNsgDV89dqP9TzgYW4sV4TvhdDJYMNtM2bN9MZEjmUmXMKmIcZFhbwMTExhl81+3vmUXv37tV5KidMmGA0Ds1OUC0N8jzn8YuPj0daWppO4TdWwaulWaO+ahZBzkSzS4HXyf38/DBv3jyjiGhK5by8PMyZM0cH4siRI/H+++83pblmv5aF0g8//KBjru+8806zt9+YBhPppDhm+jdu3NApXYxbSylsAbDyw+Pq4OCAhgryv5v+s2fPYunSpTqrZPhwSjdMmndLKczskpKSEBUVhf79+2PGjBktgrSDBw9i69atOgFwL3lCfTfPc4uXAVmgPvvss2gpCsauXbuwY8cOBAUF3VP+WR9W7HU5dOiQzmPDygUrPve68HYsVrxY0Zo9e7bOS3evabhbf1euXMGFCxfw5Zdf6pQe9nAZejbudn1z/N4sUessyNk1JRQBAQEBAQEBAQGB/yUEHB0dERIScstLx16ue22RN1mQM8H8MnY95n9poIV7FRAQEBAQEBD430CAvT0PnCDXD01L2TKhp0f4KyAgICAgICAgIHCvEWC3+gMpyDlIgtfIhSIgICAgICAgICDwv4wAB9EaGwTZVLya7FpnAjhynLcnCEVAQEBAQEBAQEDgfxkBjvLniP57WZosyNmFwFs6MjMz7yXdQl8CAg8vAvRMkW/u4b0/4c4EBB5iBHgXyb2OWm+W7WfGJ0bQoDw/EbtXr8DqP3fjwnUR2vUdiamPTcPQXn6w4vO/axZ1Lo7++h+8t+AUQl+bhy+e7wKF2PiUjxp1GW5cCsOqFauw49B5FCnaYvDYyXjs0eFo72lL55RX71ijKkLciW34bdUaqn8JUo/uGDnpcUyfNAQ+DpRBqnr1JnzSQlWSgYh9W2nf+XrsO5OO1kGhGP/Y85g+tisczCpTSVZ2oEFpbgpOHtiCtWs24eC5G7Dy7IQRk57AE5MGwMfRko5EbQIphpfSmeyl+Wk4c3Ajfl+9Badic+AQ0A+THpuOsQM7wdGKj3itvWjK8xC5bznm/nIELoNn4u3nBqK1vJaxrf3yBnxLiW0KrqFgyxqU7giDJoPyGQT3hmLiVCj6+EMkNaSMkqbEH0DuvB9Rcf46oKKUnLeEJR2649IDNp9+AfOOzbH7ggJAy3JRcvogiv/cgoqoGxDZeUM+fCqsJvaFifWdiSK06hIoY8+gcNN6KMPOQKs0g7T7aFhOnwR5EB25W9sz0QCE7qiipexhNy6hYMMaKA9RP6XUT4+hsJg4DvJg6kc/cbQlKNg8G0WLd0ObT4lpGCveMy2hTF5SGnMrJ5gOmAzrp8ZD2vrO+7mj33q/oHGkuV98aBeKt2yH+mouxG7BMB//FCxHhUBcc85o1ajITkTx/u0o3X8UmrRyqt+e6k+BRb9giBXGZxurlTzCKjctGvs2rMLaLWGIz5ESnxqDx6Y/iv6dvWBZ47hmTUUpEk5txvLla7E3/CoqrH3QvfcgjBozDL06+cHWnFJ4Gk7JWjut70vmEenEIzZj9bpN2HP4MkzbED+aMBVPPT4aAU6KO597en6Lb15F2I61WLn2NBSBoRjYvze6d+tMfMIa0poMr77ua/2NaCrNw9VTe7CaeOSuY5dRau6FgWOm4PHJI9GlrSPkkjuf+YrSLISt+A+++e0qejz3Md59OhTWjaWF5kNBRiwO71iPteu34HhcMVyD+mDCtCcxdUQ3ONPR0tVxJ15QkoXL4bvxx6p1CDubArlLZ4yeSkdKj+wJT3tFjfq13vgdX/LOLc7MyVto77VrvVkE+R13VO8XWpSkn8Q3r76CbzdHohRi2uRvgpjLF3Hy6Em88Z+v8fLYYFgYDio9UDkxu/Hdd2sQQXnMYxbtxIvPhCCwtlPF6utbW464gwvw8sxvEEYCScz5g3GZEsqcxMnzifjis5no7WNN31UWjTILR5Z/gjc+XoWojHw6U5wYGG36v3gmDOFRn2HO588i0K45mIYW5XmxWDfnE3y+dDcSMgpgIjXBldgoHN25G+e/WI45bw2CnU4waVGWfRUbF32BLxdtQ1wuZV2SS5CWvgVnD+/F7gP/wJzZ/0Avb8pUVR8WDfpNi+KsWGxY8CH+s2gz4nMpExw/lBfP4+Txk7j6f1/inel94WRRCwY0ZllJp/HHsmVYvysNXcRtMXZ0P7T2aDpVlaRTFqrMs8j+6ANUnK3yBhGTrAjfgvzIM6h44wtYT+hAgqnqRrVFKD6wDhXnEgFOmCYy5KgkeG9eQPnFVJh3IEFu+FODcKpeSVN8A/lrvkfJygOgQ+l17WnzclCyKBKqhPfQ6oOJEBsca6tVUia7v9ahYM6v0KaXVPVfAlXYCuREHIPl25/Cckg7iOhc+6YVUqBj9yHn//4LTVJVBkFqUrnzF+RGRsP6vXehCPWkdHzUi+YmSsNOkBAvJyFe1Sul84WG7qdMRQpAPMp3r0ZpUAikI/2aQBalAc2PQ+6iWSjfdp4ULFIWiCZNzFEUzToJVcq3sH+tH0R6TkXzqjzuKPLmzUZFxA2ijWii+uqb11F4/i+opn8M2+cHQGyuv6CRpFE/mbFhmPP+v7F40zkU0HyR0P1fPH8a4SfP44P/foJpA/yhqOJT2ooinF33EWa8+SOickWUWY2Ex7UUEhY7sW7lIgx54h289/pjCHG3avT0qihJwbYFn+CDBVuQkK2k5Ux67iJ3Yfbxbdiy8yV8O/8zjGhHiW3004QEXH7KSSz98jN8v+4IUnIpk+GeHVhOaT7sfAbhra/m4q0J7W/dQ2OQUpOyfmbbXLzz/kKEp5QQTWTcqK/jp8gTOLD3MP71+fuY3M8fFoaKKGN7dRd+nLMaB64BOTb7MXFcN4S0asyYaZCXEoFfv/kE81YdRIZSBjnxzpv7lyM8bBf2P/URvv34CQQ5KqpwJyFecAP7V32FD7/8HeeuF1JuCDG0tA/8xMlwXIz/BJ++Ph4+reRGjxMnv2ps4rDGYG94DT+y97ao83Fo6X8xd/MFqK0c4RPYBb17dYePkxnSE85h27qtiL6pukWTurwQqTFHsHT+TzhxnTbaE1NRUni/kt8YWVTZpzDnowU4lFCEVq4+aN+1J7p1Jk1ZlIULx3Zi24EoFNxqV4ObkRsxa84mXMlWw9HDF9369kdokDtkpM2d27MSm45dA7G1pheyfi5Re4vXhiGlUAxnr3bo3a8/2rdxgkSVhu1Lvseh+Kp0onQoS/LFQ9i09TCulVuj68BJmPnWW3iGLHE/VxOc2/o9/vtjGPKUxmWcqu0mNMoiXCUB8+MvB3C93BLu/u3RNZQUKO/WJEQvYOufOxGZnFMLBvSwFKXj5M4/sOXQVZQpVSgrKkRJmfKWTKitP6O+Uxcg/495ZF3fJMFDDMCyNcSeJITYSiq7gdI//4Qq/fY8ImmBimRKRUrjK7Jyh6Rnf0j7D6p8DRgM2cQXYDGIBJKeCRpFjEFlUhZLz+1B6ebDQCmNgYwYtyvRZUk59EUqqIjBlMUYpOElpqZMikDRr79Dm0GZ3CTEQBw9IXZ1BMyIURPzLj97BZpyg3sx6M6otxU5yF82r1KImxDDtaPc1U4UpErwadPOoXj3X6goqFrbE7vC8snnYDpsMKT9BtKrEitJ944gVxh1S14MU0pVa2XcQRZ30KstRXHYWpTvu0BjQ+CbkQLq6V1576RxlW9cjPLE26l0NYWpKNq2lpS3dKLbGiYdBkA2fhTEXpw+uAhlaxaiLDr/jm6M/UJJFuORtT9g+d5L0Ni0RkD7TujRpSPaOCiQejGMBOcRJGffpqswfis++3AFogoV8OsyAi++/S+89dI09GnvAU1WPA7v3owDZPmVG8+2qkjXIvPiHqxYfwTpJRK07z8Br7/3b8ycPgwBLtZIPvE7vvhyFeILb3OkiqJU7Fv9M1ZuP4lMtTlc3Dzg6eEO59a2KExiJeVT7Lxa2IRnkqz9nCvYsmINTqeL4dfpETz96tt49ZlxZIlb4frZbfhx8QbiEfnQrxhrlIVIiT6CX+YuQVhcFk08ShVNXlJ2kDWmaCsKEBO+C1t3n0GBzAt9Rz6Jf7z9GqYO6wp3RSH2/zYL8/+8iHJ1FfCacqRe2o0lP6xHVLYWzm0C0aVHD3QIcINFaSz2bdqCv6JvNGqc+CAhY/O0N+aea7umMSrQHe1wCsGGuhLUpeTm2XUZBaRJtxv4D6z4YSYCTNOw+uu38e+5R5CbSWnuskqgdWaXrRLXzmzEV/+diw2Ho5FbXMnMNBoVKvQz4w5q6vpCi5xLh7A/JhMKG09M/eBXfPp0Z+Rf2ICP3/0Qa6JycSM5DQXlGtiQh4B8o7hyMgwx2ZRf2y4E7/30M14a6I6M8CV44fGPEFGajfhraSjXeJOm3jTurynPQOSJi0i7WYhW7R7FrO8+wqRQdyRufAeDp/+IovwYxNLDoA0wI43PBObWzvANDIFpaD+8+vqz6NXWDtqiBPz+2ct4/+cjOEUMOfGj0bCjRP5NKRVlBYiOOIpocll7dB2ND7/9LyZ1FmPfj5/io3kbkZqQihs5xTojytB7pqkoQ9L5nfh15W7E5vOYSaFUlaGknE3hJjL+qhvSlCZAeSyRxkkLsc9E2M9+nfh6IXIW/hPlG2LIkkxCxU06GMOVhCEVTXkBMVSydkm2iv0HwvqViZA62kFsSZq63p1c1XZT/mgr8qCkrHnaLLJkLX2hePldWI1qj5K/5iH/0w2khWZClUQKRefKlLJasmhKT+8hdzIJH1N7yEa/DOtnR8JEkYfiwztQFp4N8yHkXmbrq4lFXXQJqlPEPMVSSHq9CPv3p0FTdAa5s77UeTU0mSm0VEF021DgKpnA5t0m6163utXQGJ78HXkfXiBDmNzEXl0h8ydFoAlFq8xAeUQ0KSxqiFp1h9X775BXwA2FW/8PhbMOEl7XoLpWCLkfH25CbtzMBKiiYmgcaUngkRmwfWMKufZNadlkK7Je+wra7BSUkcA072LfFKqgLEzEybDzyBbbocfwN/HdrJcQaBKNhR//HxasCce11OvILaKDVhzpmSQ+FbV/I45ey4ed3+OY9esPGBdoTYpJLk52nov33pqLWBEdTkR8pSmsQmbphLaBQRB16YN3//0CepDyYkIK6iP+r+Cx9/9EymlWrJ+Hf3tm6xXIuBKOXftPID5DhIDBU/Hmq5PgbaFE4unNmD1nHS7FH8Dvf57HKFoqM2+USSeCCSlzHqTg9zd1wbPv/guP9nKDuCwDB8lt/sE3q3E14jwuJ2chhDyEZmI1bpz5He+8+x22/hUPVoNE9PxqiZ+rG2l3iEiJt3JwR0DHHvAj3vnay5PR3kWBsswx5MV8A3O2nsWRg6eR9VxXuJlIoFGW4tqFUziTXARHr554/fM5eHGEO6I3zcI7n/+C8LQbSL2Rj3JS+OXVluYaPp3YvW5sauqGt157zSYLcnYlcIJ+jlxvSNGW0QNrZQ1Xj3YYMnkcOjiaIu1CDK4kpEMlkcHMshWsiGnpRCNZqtcunsb5+HzYuAXAWXUdV5Jy6Dc1KQ7Gq7Zs1NiQFWLu3h/jhneBpToH52KuIpU0azNzR1jbWUJGbpbKQpOLhI6dfWs4tJuIsf28ICFLL+r8JWSQa1FqoUArG4smC3HuS0vqqMjcAnat26DNsOHo3c4Vmtx4RJxLQBlNdAnR1spGvw5pCveOI/HR9/3IgCE3krgECRdPUa7fWFxN59zhEshoIlUhWHUvjftDjxi0tPzg4O2Dzn2Iro6OKM08TWN1A4Wk8Fi4WcPa3BS3INN1o0XB9XNYs2gZ9kdmVHVceYJRaXNYlVUtalU0j/hYQ7kp5GPGwtTFjNzGEaiIJ0HFbnMzEtIWt6e3prgA2hJWKkTQxB9D/sJkOmrWGaZB3WDWozMJfBv+qemFORLNY5HCAibBoTDr6gdtOWn4l0jp4DkrpvU328oTt1gwqQszoTxzjnzD5JZr7QNpW2uUnj2ks3alvsOgGOBEQpwUsmagTVtO88yC+pbRKXvDB8HEqgJlUXHQZBZR+xKILG3IfX8bs5pgqAvTULxtG7QFdB9WrjAbNgTSRrlDb7esJVe6yIwUBzMrSHsNhDzQlZwnibTMkVJZSWIDsWFMgYqUfOY1jKM10SsqofXyPKjzyJuhFwb0zDS1aMlTIpFY0TkEDug/cjDaOYqQdioWidezoBSZwYb6NpNVKVdaOnjmZhY5YDSwcwuEr4t55XDRPGSGTiNLyiL9rf6gGEmiCPaBI/Dxgl5Qm1qQq5qUZXruU9JvIDIxXxdDIZErIKsSPlpVLq7SMsAlWoqUOLXDqEcfx5jBvWBPSzq9uzoh/kAYovfF4vzBk7j+Th/41YxDaBB1IijsAvDcf5bh0TISqBYiZMZHIi4uHpFxGbwCA1OFDKbk6uZHEoTptfNhOHalAI7+HWBO3sa4FDp4hnBrDD/XkSi2QECfx/F154n03JlDUpGNy2cjkZJ4gZYSSqldGRQsWEmR4sI8TUNzvZWzJ1y6DcSgnn4QF8TjytVrOkORz1CwtpLfXp7QXWXcfx4eHvf8KNq6n1ojaDdG+5DYBeMpyjnunmCOwYM9cfPKYfwyfw7WHLwCuVsIej0yBAHOVUd5iizJap+MF0r9IPUMRPmxj/H2wgjdYBj/qIrg3HUKPvzQHiUufdDZLg8nd6zA/B9W0zqJFv79QtG/TzvY6tchRVboPOoFvGPWC1bth8C1IgOH1szFVws2IrbcCl36DsXwUG80zeatBNnEwh2Dps6AaeBNeHbpC6uyWGxcOgtf/RKGAoUTBgyfjr4BBmtrZA1ZWNNaLqkaKaf+xII5P+PAyRgkp2eR1WuNUY+QW6lacJwRg2lQVapohX6PvotPvdLgEdIXZtnnsfanheSqO4U8iQtGDe+HYA87Uhpul/K8eOxY/h2W775AAssF/q3lyE6+Tho3BVkZ70a53XCNdyY2AbCc8SKUSRJaP/aFMvkE8hfNgzqSBLmpA0z7DNUJd/1lmqK8SkHOFkBOAipOJugEq3LnTpR1GwrLp56CeYgbCQj9FY37K5K1gmLgRHI5d4LEvSOthWehYN1SlG06qxPW4najYdaex44LMbDiNKjZQidGpyUBVrz8G7IqC4gpWUDs4Q/5wDGwoNgCKbl0myrMJa1IeZ35MikPpMx2tkZJxA4U/rwKmhslENkEQt6zOyR2dcxoWm8tj94H5V+phBEdadmelIzevk2mSaxwgcW4JyDxyYa8YygF+SUg/7e5UO6Jo7apn64U7OevPxCHBKONC0xcnUkZS4Hy8B/IyQ6neiVQJ5IXJI8kh5kP5CHulfA2+n8RzG3bY9q/P4R/mgLd+rsh/fweLF24GDtOJUPm1g2D+/eAhx1b41RIsHsFd4Cb9QlkXt6OxT+6YlT3NjBV0vLSsUjcoOAn5pG8Ftuk6UUCyNKu0tNQnBiGuR/NwuHLcbgWT0tJcmt06fgIAl0rx09dkodrideRQcKsdddAdOzgBeuquAwTCy907kJLUQcpNiEpGqk5avi5NJIyEpAyhS0cFBpq6yTW//g1fqVYh1Q6lCYnX4YeU4PQ1s0WlfqFKQKHvIh3MikGihToshPf4MOF5N1hxct4hn5rdMVSM1hRQBu0xYjavQHfEk//KzIONzJzUSbxoIDD9rCv8rqxB6Hj0GfwobwHzP16wh0J2PXbj/hx1SGklFggdORAdA90pgA94zVnvVeak6Pd67XyZhHkTHSDw+3FlggeMh3BNHKZV/Zh0Tf/xc9bI1Bi4YdR02bgucm94XjLz2OCVm0H4AV6ERfG7svkBqW+WKtqzMBLbfwx/jl/VJTdxKmty/Dt7GU4Ep0Hl85D8fQLz2FIJxfcjp8TwcYrFI/PCIW65DoO/P4tPvn2d0SkahDUeyxeefMF9PQxEK63plUj3hAj8Og4CI93pOCyjAvY8OM3mL10J2KLLNB11PP44N2p8LPWR20Ztk840HwzoaMr5eZmMCfruYws5YzoCEReewQDfPQM0PCahr8Xm8jhHjwQT7RTkTA+h3VL59OE34eUMkv0Gv8MXnxsCNrYV1kf1Ky2LBW7l36B2T/TmrraGj0emYbRwQVY9cMaFGnUUDXWf1YbySILKPpNohetx1/7i4KfvoXqxDUSMmTZ9Z8G66n9yZK9/TCKZBYQ2dN4Fcgh9m0Hias51DcSUREdQwFyfyKfAoFMPv8XZF5NdP2LpDD16kKvEKhzE1CwfilK1h6i9XJaAmhDLv3XHydhqVd9NBQ0Rksm+WRK0lohSm7SZ6KZzReyqDQxJ1CSnEiMjizAab2bHo1tYgPLEU+SB6gEpWe2oXDxz9BQ0Ce5qCCb8AQpIBRQpyetBuba8nQUbd5MNFKMgS0tGUwYYXAfNSob85Hmvjy4P704ePES8n5dgPKt7KEgN3TQWNj841GYWN4eRwkph1J/X6iOJ1FMQQxU9LpdSNC3CYVpE+c9t2cis0HHQVPRXlVMy0S0pjp/PlbvvYgKqyBMevolTBnWEXbm+mfSBD59n8DTw05j4dbT+OXbVBzxIm9PRT5upN5AGikYbiRIJLQE2UhxefsWq96x7BNLTCGj/B3m1iKUkLepODMKkdHp8OruSl6LMuTmF6GwxBTe9g5oTbEMemrJLQMHJ2syQsi3WXod2QU091zu6KIRX9DcIPe1TE6eVamchDcHol1FdHw62pP3zoLiV2x9B+OtTwajgpYmt0brvYw6jt6I/mq7hIKniR+amckho6WMcnLnx509jdicTgimXUYcT2PfphsebROCosxY7Fq5GPN/2oTLWSIED5qGV2dMJFptbmNVWxd1fMc51vn0RmNPqqujOaO+bjZBztlsWOts2E1okJ94CAv/8zl+3n4axXJvDJnyKv7x4ni0c74tGKrfCbmnbj/POi9l9d8b9kmjKsDZHcvw36+W4mhMLlq3G4hnXnsD0wZ3JGv8zseMJ/q+ld/i49mraF2lHH49x+P1f72N8b3aQG5AT8N6r69WpRBfv+hbzP11F67kSdFp6HP45NPX0M/Pug5jTAKX9iPx2nt09GFcLK2zh2Hrll2IOPgrFvwxCF3+byAsm7Iox+SSOywv9SI2/jQPi37fi8QSBXqMfAqvvzId3X1b62LL9HdVmnIM3y/civMp+eRSs0MeMdljeenIpODECtrGs+2X73DjJAXyDR6K7kFupHg0FcBKIZ777deoOJVKApBca30eg82LkyDVe3WqiJM4BMPymRfIbWsFs86daF3VnJYwr6Fo5xIU/7gPmjjaKnZoImRtOumUI/09Ne4vucxzE0mI/4RSCmBEMbmP3XuRNfwizDo4GrRP90+M5daeIRNTiL27QBrSlrIspUN5+jgFoZGLcvMuKPt2pHVisuSbChkF+5Rd2In8H5aSECdPgNwRsjHPwGpSf0hs67DGSWsui9lDilI6SzhIQsfDvCtZvU2l5Ra4JMRvkhD/hYT4jjOkxJDl6j8cNu+9Apm3oTJKuOZloCKJFDYOjDOn5RM3CtijCHVtVhJ5FvKhST5GSxMTYflIm1utN/YNbydLjdqHxXS64h97IlFu4YsxT76Cl58cSltPybVv0LDMsSte+uhTSBxW4uCZy0i6fh05WhnMLclVW1BKfJGWwUxp+cLgmqa8tWjTF+98aoMrFBkfc+YAtm7agZOntmLZz13QJfAZuJP1LzWl409N6WhSEi7KaglKKMCyapmLeXbzWI9iWLt2wpSXPkb7flcQc/4Edm3bgROX92D52m7o0s6N1q4tq2HG8T7EYKpeTUGj6lqRAm37TMbbrTsiIS4aZ47sw5+bD+DohkVYRsGasx8PqnKZa1BC2xf3rFqEuUs24iLFAPn3eRQzX38Bj3T2gFkjpSKfesZ51uVyClg1FFbNcGt3a6KRJFdvll0KfCQmnwnt6upa/cc7PlECmWtHMe/D/8Oy7RRoI3bH8Kmv453Xp6KT5+2tX3dcRl/osWHjpVGFImQv71mCzz5fgkPR2bAL7I9n3/wnnhnTDa0Vt/TVW01ry9IR9tt3+HTuakTQ2mubHtPxz//7N6bStpNq2+NuXdH4N2XZ0di0dA4WrNiNmBtidBj5LD7+5HUMDnbgoGKDokVpTjLCj1DUeoUb+g7oBZ/2ofBt3wP9B/aGM5JxZfFR/LX9L9x4rz/8ZXfel0Fjd3mrQRHtQd3881zMX7kHycVmCBk6Ha+/9hz6t3cl91P1y0XErBTyyv6UxTm4eGwHLlZVMbkRi/0bU2g7nROSS63g6T4eXrZ1mH/Vm63zk+r6CeR+VyXEiWlKek+HzavTYOppdcc1IlMbKHqNrva9xN4bVhOeROk22oNOSprqUgLxlaYLcnVBKu3B/hml6w9CW0hr+bRH3fKll2Hew5uWog3ZPwksC1oDd5WR4C+FyCEIFi/8ExakJGo1eSjY9DWKl1AbJORUtE1G5mN7eztdtTtp6IdKgZw3dxEJ8TyKQaTgulEzYP34UFJsqpazamtKfRNF69eTV4F+tAqkPecDyTvQXCKJZHL2FeSv+AHlO2n5oYysav9hsH7rFZgFciS6YSGBlBwFVWQiLT3YQTbiOViM6arbalaRfhb5C+aTyz0JJTvPwHJQm6YpGhSAdTP2MJbM/gar9pxHObnsRzw+EzNnjEWQq1UtFpsJHNsNpa2q/hh+NR7X0mjNnNbyk06TcF2xh4SqnJ6Nps33CorYP7Z3H66UuWPYiN7woOfek14DB/aDn1UxZny0FXGUuyAmfTo83azg4mQPe4UaN68lISGFthP624OdCJryNERfzKTIbA0srbzhbG84Jw3xvvt73lUUHb6D1r2BrkNp37h3Bzh7t0ef/n3hY1OM67M34PLxs4jLmIhAZ8vbHk+aPszP9T2zOG9coS12aTE4GhaOQqtgDOgfgna0PNkupBe9p9gX2j47a+sVHN5/DnnTAtGK7r+84DoO0u6GOYs24Hx6hc44e/XNlzG6py+seNdLI4s+x7pMRjEyemHVyLaMvawGKzb28sr6nBAmOztbd1Yzh+DXV9TF8Vjz9RdYsuMUck28MPKpd/H+m1PRuU3D3RmNG3Qtci9vwmefLsKRy5mwbzcEL9O5xM+N7V77PmiKqby89yd89f16nI0vgk+fJ/A+RaxOHtAWlo2MZqwLF3ZbHln3Exb/voei5CUIGfM0/v3BTAzrSG7EOy5S6/Znb/x1Lvan+yJLZIvnx3aGNdFkqrCElaUUWppEFWXltNOqacy2ojQH4ZsXYf7Pu3CtRI4uw57G22+9gMGktSoM94VW0Sh37YcPZn2EtvvPI/kGrZHl5OFmegqSYlOhpIAmu9YucHYNgK+XExRkLTSlaEoTkffjArLEr1MzFJzS9xnYvD4NMlIG7yxk8WVEo+REFAV0+ZA12Y4CvSjoCyqUU3CONpv3vnCwVxPd6tSKVpWPkqMbUbruAAWFkSXu1hMWL74IRd+2lNik5j3Tuqm1G0y7BqH0MiVnKcqCKjYB6vbORB/VVVGUPwfIcSAaeS+ayhs0hWT1zl1QJcRbQTb2JUroMhxSSiRSd6EcB3EHoDxKgYtEh7TXWMgDmhIRXr0njlov3LICZWyJl5NiEzgMVmQZmXV0vlMQk3dIW1pICgVtWaG1Tql/EGQBfjrlxsSuBGI7GTQJhdDk0Q4AZhKNnv6kLNPe9g0/fItfd1UK8VFPv0kew4noWEvSqNt3JIaFgxdC+EVfqouvY2fmXxSZbUJBaLT0JavL43G7hfreFaWexR8/L8GBRCvkm8/Gq6NorZkEj0RuCRtynYsqaKmGdhbwVi4TmR382gfDl2JY9iWcwtaN2xDkYYvu3jLE7luH9cduUBpRM/j07E0Ct+a8rI8Kw99IMSyiZUfKmTAvTI1huVZwfWM4nGktXio3h4UlLWORhKmg7acVvBZQs7Aw131Hv9Xyc83qtX4m4+x61CGs+v57xFj2hcry35jSj+IkyNo3s7CCJQWKimnbp5JoYPtPoyxGzOFVmPv9WlzIqIB/r4l4jbarTewXCJs7ns9ae7zrl/q18rtWbMYKzSLIOVihoWvkZcnh+J2CIdJoXdC8tQU0+ZH4fX40VtI+PxPKGiU1lcHeowMGDR2Mzr6U3ODWzVK0YZUl3jhvsRrRYX9gb2QySsVmcJSpkXR8HWadXEcDzG4oWtuU2yCwxyAM6RcCZ/M0HN+8B1FJFE2vVtA2YC3O7ViCyO0UZUmTxJSSw8hp73L70EcwpD+tl+mD5G7R2/A35Vlx2Lf/FGKSbpLm7wlTTRolLJiDA7+RNWdCdFFfZtZ05u3ACRRg5w4LG45iVyD7UBh+/q4cNy4/Ar9WGsSfOYo9YWSZFMvRa2A3uDVJ4aCHtDAZx/cdwKXUPCha037Y4mvYt2oexQvQei+thfGeSTPayjdo3AT0DHCCjLZPdRv9PHx75aKwuBSlBek4tW0ZvqKtLsUeXcj78Q4mhPrA2cWZ1hcbr/kysqqUs1AeTyQuQRyA1vIpZB35P31F3JMmCbmoRRRwYuLYFuYDB0PeVobiI2tQ/CtZtyUmKHILgrQd3U9eIiUViSKrmdqQucCsf/vbJkLDh69aTU1RGm0ZI6GcXU5cioNeClEWtgplh6gP4moiimMgjYsCyyaR1ehL1qQDzPuPR/mRGGgoOKl05Wco30PuYpKtmuvJdF+kDNDzYOpBXoZGC6ZKEstjj0B9IZsapoaIFvWNcOQuOEVMlKOqSWUkq1Hq0w2Kwb1pa16VcNcWomjrOrKUGSNPKMb2I4Wk2i036UNFFkWo/0V+m2KSPrReTu4HFG9ahOKNNI4U1CmSEmYWDjCjjGqKHm4wsafsc/ZyaBNTULxyLlQxnSgsghj1hXCoL+UQLRQl3a2J40j8rICSjOzZFYk0ijt0tJaiIDUCK+ddpHgFhk5Cz6QMdrTWOn7cIPg5kYVey9ho6RSs4iLaJ0+7Hm2Jr5kRj2lKMW/lDA/yYhUfP41FX3yA9Kih5K42oTX8I9i16yjyKQdBcNteFDVP/Yhl8O7cF4N678H5xEM4vmk+XorYAlc7iixPSUJiCiXEcgjFE08NhH2jl7hExDet4ObmBGXaXmynzJvlWefRzdsKN+MicODAEcSRxdtmWCCt09MOH0OMCEcWeJUsvQlKqkgO61ZOsCXFN+Hkdsz/ogRxw3rB1ZSySobTduPDcSgqd0BXCnizoUFSFefizOGtCI9Lh9aKAv7U2YjY/hNotYkwM9HxNJl5a3QbNh5Du7SBeSMMjgdWkPPWs6ysrMqtFrTmUl+RKKxupRsty43DoS3XdHsJNfSEiCgCkq0OiWU7pJXZwu2VwTrtrrI9Cojgp4gLWQa81du4IqbIRlrTpZlToKa1r8vHsCH2L12b1DP1Sy496t/p9HWYObphfAhFQrai9XpdR0WIPbUTSRFEA1lIbPGK6SUijhZ49hpsPb7AkADLRvNZCWmvdrTljp9zFgTnDm/DxSP0nu+3qi+x1BoBFAPk9/MbCHTrgFHjxuJUZAoOnwvDr1dPQmpCe2zLipFfJIb/gBn44NX+sKqNuxgBmpi2+FhampOao0FhLm1zObIdl44Sr62iizETmZjjbIk9fvrXODhbyoj3msPekV7Uj7bMCplnKKqdA2As7NGmbTDaB5KQMoKGuqqKaXsXB2bpZoSGkr1EHGLCqqpTD9yJpBW5rC1g+ia5jimhj0hBgjyL9pMTXuVxp6k+TQa2eKUkKJ58mwSFU13dNfh7Xl4Q6beLkXtWkxpFAjmqilBqhjDjojpRCrOQj2ldWgqZXx9YvvgUChashPYGnZyUQhHbXPh+zNxhPnUcJJR2t6nAiS3JW8GPJ98zLRtVhGfegZlSTl4L2ilhNboDP2a0rzyKkrWk6Og36TQOZsH6iHsdhU3+T8zriXpLiKxJzdXT9DJolvGigVYRhPKgV2FKMQRmI/qSUrYP2uuUjW/LJfqd7oe1fI0EJt2foOWSYIMGGvGWupSYWcBSQQBQspLstKs4tC2J4GceRN3xvOc6in1QkSL7jwmdYFWLIq9RK2nNlFLv0tZCU1KSzMgirxz9RtBEl5jaB+PRpyfgxKVkHI4Ow/Lk06Bld91zX0hBiO5dJuKV16eQm72SOZq3Dsb4p55FHBkja8Iu0rp1BuKpvs7oUvjg6fc+xfQejgbGkvF0mSrsETrmKYw7dBm/HTqLP3+OxU7ablahLENRUQWc2w/H88+Ohb9T9fVx7om3nZFJQFhSEKDR/FxPqwSt/UMxbtJwnIn7Def/2obk8/tJsaJdFiUU7FdqiR6T38Kbk4J0O4yUvOPHwhYymi75hTm4cnofEs/SyBrydaJnX6IJ/L55njLCEZ/Rd9XAvxzwdktWNfCaplajYW16YcLz8vJ06+NeXl71Nmjq+gg+XfAx7JasRdgJ2nOYnlutvkhqA28/D7T1d6FcxgYQkrYe1HsU+gTk0LrYEHjVsqZdraE7PojRdtz7+P6/5li+aT/OXI5FFqUcNSzm9m3g6dOWsjfRHmATS4x49RNkSn/Bhu0HcCaK9hkyA7xVTGDj6EjJEGjbCVkIBpTeqtHQNxLbdpj+1jvQ2jti065juJRE7kalQcYb4qg2Ll4I7kZrPOS2Eptao/OIGZhl54kNa9djx/7jiM+TwDtkAIaOGo8pk4ZR3njaY9tQAmqtJ4Lctg0e/cdnyJcuw2byGFxNSAM5NqsVB+9AdPInS405So0iov2urkEh6NmzK3I9QxHcpvmEgMSJtum9/wqK/thKllgyJQ4xwIvpYKVQQdvQ/N111rlZyGRIvg2mNK27UXaQ8nMn5kBkTRneOveBYvR4CoDzrJY2tcatNPijmLYSWk55nvr/g3Kmn6UtUWSO1SCNOoKkUweYWFQqvSLK/qboS9HsLkGUXW0bJbqJoDwClA7Xi6zjKdNg3rvdnfnGG0zR7YqmbcbC8j3aC752P8UEkBCvuR2Q5pnYsQ0pPfY6dzVfKTJzg7SrF1QXrGFFiWrEzRvhCRPa9mb1Eo2j9Toow0koF9FyguFjxkRQfIO0UwB5L2hMJaRkTPoHbe3rgJJd+1BxIY6WM8j74kFu9gGjYTGiZ/3r/dzeXYsYNh6D8M8vP4B8GfGpU5eRWINPAdZoGxAMP3K1m1YzNW83LlHYIahLNwwYXIo2/QfCy6FpFjnPG78BL9DarifWrd2AHXsP43RsBdr1fASDR4zFxAmj0dWP5rz+wSdDw73zWHzwrSs6bd6AjZt3Izy2FG17DsFjTz+Px0d00e0rv01xI96R5e8UOJiSeS1EwOo/sGlnGKJSCykFbA9MHjoaEyeOQmh7T1jWiNURS8wQ0H3N8kAzAABAAElEQVQIBvQogeOgAfCxa7Qkh9TcGQOmvY25zv6Ey5/YeyQCmRU2CB44BiNGT8Lkcf3gUxUDYkpbagc+9T4+K7XDmp1HcTme+DrnRTAo1s7BCG7nqzOu9FAa/HzXtxzw9sAKciacNdW7Ra2LJAq0G/oSFg6cQZphOcoplShvWZBSlCVrvBXkGmU3n5y2MFTPmCaGR/+3sDX8dd3vkkZYm6aUaWvyu3Mx8S2O2qQ1ZHIxMr0cuamlfc6cxY+DUuRkGvMAWnn2wqufd6doVFpL5TVnCnGRkoXOiR00alqvo+ulcjNyKTd+EupmBT0MHp1H4r32Q/HPryidKUWUatnNw30RIdxXhYbWfMzJ9VnFNCRmrShN4xRSbibifVKk2KPM2y4khCXnQ2/MBKw5Q3XbzzqMxIc/DMW/qA8VrTMxXZwbn0WQWk2fyX3MUZp6uqq1ITaHT+hjWLhxsm45QkpYNwdd3Ad7Aiz6P0UBbI9TYD2lfuUoXFqa4cQbOguNB5MFkxlvOaELTMzogAkKfnm2I7RP/lOngbMHiDQ2uobGr9kII++DN22BercbtG8SXYQZE6Drg+mgbXhaNXl0aNsQW7yVhSw8drcH9IKsbQ9gJkl+5i1kGeg8Qo1bS9I3fuuvSEoxFOPeooNIXifhR7SRINe51HXtk7VJmIloS5OYg7Kq8BCZuqPV56t0yggvVzR7oblvRvNeHjSIaKL5xHjxEoRuHKk3xovmvpjmPsFBpTJA0GIgHYxD2w91Dy1/3cxYmchIWR41E4uHvUTzvpxSQhNf0j2TPGgaqAk7MbnX5WRlM6m1FbHMHt0nvIPVY96ia+nZrBboWNsVd//OxNQS/j0n4P1uY/AezfsylQgySkyje+6JEPYUGBYWmM7+vfHMuz3w5FtfUgQ78TxSuvlZNGmmeWUiVcCDdv/M/LwvXvqQ+AQxIzE9i6Y6Xsk8rAZRRCB77oKGvYX1g6r4eZOwob3slKCoJ23V7Tb8aXxFc5uOT9Lx9kr+Ts+XHhR66By8euPVL7rjxU9JDii5Lu/xZzwqea2a+LyMeBonsjGmeHl50bkdkbpDU+71Maa3WIkxBNes29D1cf117ErhrRG8Hs5JnRpa+EEyraHZNfTaynqUUpCUBH6ZyuqJ0tU3ShPwVn1yf/+thYSKhNbC+dUQ0pgWFkT6a/422gz6MGas9PTox1r/uVn/Em0sXHQCpkHDQ48zzSERzb1bD3azElTVGM0bVk75RXF4DS9V15Em1vBrjK2pv3969hpW6F5IuDfJ/3q3jngcqQ9dPw14LHXNVV3zd9KlE9xVfKpB06uW++QUoqa1eKtqqdrwrwyeyQbxCkM+1tBhbzg1lTX1fdD5AA3toun8vDqRIjLIpKQYSknBqrcwrcRn+SVrDFOro3FOVc7GbEkJZR+8tcxXR+Vm/roOXbKZexGaExAQEBAQEBAQEHiIEdAL8vtxi80myM3JVcjlfkTscb+VASh/q53F3TSqMG3svm9ppSVjxli1RMxaIk36edVSx7MlYiZgpZ81d//LWN3v0hLnUE1MOIcK7yFnt/q9tsib7MNjgplwvon8/HwkJCTg6lXDsNOat9s8n3ly8fYn7pNf/JkPdE9KSqq3A73CUW+lZvyRaWNNjU/EyczMbMaWK5tiDLh9Y4o+GIOx4Gt5nailFA6c5PnEa1sKOhSlpdDGNPEc46RH/L6l0MXjpo+S5VgFzvNsDG2seBtT35h5wvOM6eGDKAoKaB9XI4qxy3Z364KDcvme+XnktnNyeMva/S+c3pNp4mfyftJkiLeeDqaJ3cV/B/+6G/I8b5hH8XPHO6N4PrW0wllNmc9nUH55fhY5pwrziHtZmizImVhmcHwjnKJu3bp1uHiR9oX+zYX75InPwMXFxelOX9u7dy+io6Pr7dnZmRJN3MOSmpqqm4ic+e7LL79s9p75IWMGbkxhBst08UN78OBBxMfHG3N5g+vyGBmrZLBimJKSAgcHB51ixmPakGIsBg1p07AO02Rrawt3d3dERUXplAzD35v7Pc/rhnq3mNlxfRcXFx2zO3LkSIPJ4ef2OqUTNabolfe7XcOYcYIopm3p0qVgYWVs4bnanIWZbnJysg7b7du34/Rp2obYAgo/j2zNpaWl4ZtvvqlGET9Dxj5H1Rpo4IeaSl1hIR0LTIoOP8cbNmzA/v37G9hS81XTJxrjOTRv3rwW6aVjoc2vAwcO6PDy9/e/53TScbCVq/KPPfYY1qxZg9DQUJw4caLBI8GDv3v3bjz33HO6PLON1bwb3KFQ8YFBgN1hxgpY9jC4ubkZfY+ssd+LwsrjvXDzcW4GQ+vo77o3trRYATem8DNvLG3M6NiiEorxCLAVauxzZHwvwhWNRUBvsDBfYO/WmDFj8D1lmmPF35jSs2dPhIeHY9q0aVi9erUxlzZPzCdPsnfffVe3l5w1fGNLTU2wIdfzNaytMUO5efOm7r2TkxNatWrVkMtrrcODUBuDYpcS98fFWDck12d3HmPELsb6ClsLxrZfX3t1/cZ9cF98T+zC5ol4t8J1WSs2pvA1LCiMLY2ZQ8b2IdR/eBFgZbCuwnaL/llmxquf++zZuhcKWl3WNSs6+qWImu5jfkb5VV/he2qMx6O+Nhkr5hX8937kD2fauG9eMuXCuOjHS/fFXf7ja//uwvgwX2R89F4TvVz6u/s2bL/+2WFYs473DKyvry8GDRpUR427f82T0FgBxtekp1N2KhLk/JddUuz2ZGHe2MI01EYHu8X1D79+UjW0D7aseO2E13vt7TnfWd2FBT7X/7sLMwx+6HmiGzKz+vrl+69NyanvGuE3AYH7gcDdhB7Pe34x79ILhnvlaWElozZFg4UBK738GysVhqWuawzr8PPJ/KM5C2PE/JD/shC9F4pOTfr5vvQ8saaCU7Nuzc96nl3z+/o+6+dDfXUMf2N89PTpv+clLp5P97I0iyD38PBoEs08QRrjOvL29tb127Zt2yb1f7eLO3TocLcqwu8CAgICAgICAgIC9wWBlrcn6r7AIHQqICAgICAgICAg8GAiIAjyB3PcBKoFBAQEBAQEBAQEdAgIglyYCAICAgICAgICAgIPMAKCIH+AB08gXUBAQEBAQEBAQEAQ5MIcEBAQEBAQEBAQEHiAERAE+QM8eALpAgICAgICAgICAk3efiZAKCAgICAgICBwfxDgPd76YuweaP11Lenvw3Y/9wpbQZAT0jx59BPIMEnEvRqE5uhHn/zgQaW/OTBoaW08jGPyMN5TS5s3DaWHE5FwYifOCsdJcDi72INceG5xYhxOPMVJcDipirHZ3B7k+28K7f/zgpwfAk5XyhnbWAjyBLofGYyaMoishPADwA8CT3zOImdsFqSm9C9cWx0BHgeeT8xk+T3PKX36xuo1H7xPnMlKf088zx504fHgjUAlxfqDj3g8OBMcCz9+/yAX5r+skPCzok97ypk6OVkY/yaUuhH4nxbkLMQ5Ly6f8KNntjyB+PsHqbDioRfcfAAGT3xOE6j/7kG6lwedVlaq+OAgnld6xYoVRWa0eq/Pg3qPzEz1gpvnGVtMjo6OjcrK+KBi0BLoZkucT0vj55yzaurHpCXQ1lw0sCLMqbE5vbXAy+6O6v+sIGcmy4dz8IuZER+3+KBZ4rUNr15T1+eefxjuqbb7bKnfsRXOiiFbSXyADyuID1thhYTvk08z4wOF2GoSlMZ7N8qsJDLeLOAeFk9PTfRYSeGzM/iIZX0OesEqr4nS7c//s1HrbCHxIQN81By/HhaBx1aSp6enTpjUTOZ/e9iFd38HAqwcsoBj5tq6deuHUogzbsxQLSwsdPfI98weh4e9sILcUo5oZrwfFsOjvnnDSjDPNUGA14dS5W/3zCLno0Z58rUUzZ3d5yzomKaHrTDGbDU9LMpJbePDLjc7O7sWKSyZ8TyslpLhWLDVxHPN2BMBDdto6e/Zu7J9+3acOXNGpyA/88wzunl3P+nm5T/GXS/gtJpSxJ06gOMXk5CZlYfiMjVMzS1hY9eKlC1HuLXxhq+3O+ws5WgJlltFSQYuRpzCuQsxSLmpglPb9ujStQva+TjBTFKdQr5XvUC/n5gzP2XvrY2Nzf0ko86+/3ZBzg/Ajh07EBkZiRkzZmDw4MEtQpjzwLAwv+361KIoMxanTxzHucvJyMzOQ6nGBJbWdmhl3xpObh7w9Q9CoK8LFNLqk61OdP/mH7SqPEQd3YWwy0qEPDIM3do6QWZS2SkrKS1p7YwtGsabLbmmlBMnTmD37t24cOECXnvtNQwYMKDFCE1WnPhlGGOhVeYi6sRRhJ+PRkrGTeQXVzJZe4fWtKTjAk9vPwQG+sHJhgJ6mgJMM12rLstB/KWzOP5XOC6lquDq1w69Bg5GFx87mNQgkO+VhQl7t1paYcPBwcGh0WRx4FhYWBh+//138JzjpaqQkBD07NlT92p0w3/DhcqcSPzy+SdYdykDRSWlUFWQEi+VwYyWdywsrGBr74iAroMx5fHJ6NfBHeb3jX9pUZpxDivnz8Wq/eeRciNT9zxYtnKDf8hAPPHii5jYPwAWkhoT7W/AzNgmf/rpJx3fcXNzQ7du3XQvPn2zpRimf5sg52CMtWvXYtOmTbh69So4OIbXdPhBaCk3X20wtQW4dGAd5s/7DaeTc1FaroRay1HsMsjN5DBXWMLazgGdH5mOF56bjC5trO6zdksaYso5rP51Kf44nIOJcIGvOykcFi1DyTDE9sqVK/jxxx918yAgIAC9e/fWzQNeW22o1yA5ORmrV6/Gli1bEBcXp1s68PHx0bVT8/xmw77v73sao6S/sGT+d9h16ioKSsugZCZrIqFAJTPIzRWwsmmFNkF9MO3ZZzC6jz8spfePiZXnJWDv2iVYtmYfLsZeR26JBgorWziv24u3Zn2FaV0c7vOcb9hoLl26VDdXOPalV69e6NOnD4KCghoclMdLbl999ZXOAElMTNSt0XLPvDbNAr2lFVVBEi5EXUOF3RD84/2BcJRJINJUoLysGHlZ6Yi9cBqnti/DlZQCfPbpTPQPdMT9mGaa8lRsnv8JZv18ElbtBmPqy13gYiVC+tVTOHh4B35epoCr2zsY5G/TIpRaw3Fes2YNDh06pNsRxIYpL535+/tjypQp6NevX5MNFMO+GvO+2QU5u0KOHj2KefPm4fTp07qAGL3GzoELLXbdltxTN5MSkHxDjK5jX8PEwe1hKzeBRq1EaWE+bqYl4uyxPdi34mvcyFDi21kvINC22eFr0BhWlBchPfEstq1Yim1hkaTZmuB6WhbKlBxt3/IEeVJSkk6bjY2NRXh4ODZv3qxb0mCB/iJp4cHBwXUKdJ5PBw4cwIIFC3D27FkdM9XPJ26Pf2/JpTQ7FXGJN2AaOAafTH8EHnZmlLiAlnVKi5GbdR1XIk/i0NE1mJ2WAfUnn2NqH3fcj/A4rSoHEdt/xfeL1iPVPBiPvvYiOntbIStyOxYs3Yw5c/ug3y9Pw830/ikaDR3nrVu36pgue6SYFy1evFjnFp82bRrGjx9f73JaREQE3n77bVy+fFk31wz75LVpNkhaXCHvolYkhrVrKCaT69/HlN1y5HGsUNE8K0Fe5hVsWvQfzKfnbu/xYeji7UC87Taf0GrUUBPfkIgNx5Y8lBlxpNBlw65NALxdbaqEvxYVKqotldziNBVlBUiMPo8MjRs6d/KCoqbrRgeYFtkXdmDhqhNQ+03Hl3PeRE8fRyhoPhWkdIeV8nMsPU4KR1QqevnZwOw2eS0C7piYGN1yJc8BfiUkJCAqKgrHjh0DGxQs0CdOnKiLt7ofBDerJOI1hBUrVuD777/XbR3gaEPDkp6e3oIZLz0MGsqSJLaET4c+GDa6PxxpNmm1GnogKqAqL0XuhBFY9vFM/HxwLfadG4uAQa4GmiPVIzkqoodBTO5Gw1J+8yL2Hk5BwMCh8LOvgpzbpf5EYhOqX1lbXZiK48cvwcynCzp4t4JpLZO5gursXz0fX32/AVfSismNpoSpXKZz5/JyQUssHN3Ma9ocGMWMUM8M2drZ+f/sXQdgVMUWPbvZTe+9kkIaCWmE0GvozUJREAv6EQT9KmBDsaIfFRUR7CJVegfpHUIJgYTeISSEkN7b1n/vbjZsSAIJCSHoG13y9u28KefNzK1zZ9Mm+Pv7Y/LkyejatWul5rN9cs6cOZqFmCUhVs/rJ96eoq/G1v+tqVxr3ghpdqyahaJX3/7wczKnMcOLrII+MhRkDUSHZTPx2Q8x2LDxKKKj3OFqpBs/amIklbRIG8BAN0jKOyYvycLZ2MPItYpA+zDaaqh5hM1FNKZo/Il1+dVluH5sF47neaJP9yCYVjOmuEh59lXs3XMYV1R+GPXa2xg9qDUcTCWQdXfFxc0HsPDIPlzOfBburg26ZDyQ18REmBMLDTxG+MNCREJCAmbPnq0h5i+++KJGQ6jfACb406dPR1ISSbfVmAt4feM1rMklIuL8+mUKeu/kaKnTcomJoEsNSZto6g1PFxtIZBdRWFQGRfnuWlXZLexa/Bt+X7IRZ9PE8Althz6PDcHAHm3QzEaOizHL8OUPO9D8yffw1ku94WoBXN83GxOnbEPQa1/jo2FBRNwVyEo6iF8++gxnrAfhf9+8hVZO1bOiBoYmcGzWGj3fHI+eYd7QDnM1mQANARW1Sy2lT9Ncw3gHyp3aGB1RT05O1piOT506hXfeeafKuGqM8VLDtK571TzA3377bXzyyScVWwbuLIXVo03XMYYnAXvk0kCiWcHEWLsg8mQwgqmFNRzc3GFnLoFKXoQyefmAo4Uy7fxezHr3ebQLD0YLYgKGjv0UK/ZdRJFGQlbhyq6fMOHNCZi54RzYmqgqTcf+JZ9j5JAR+GZ5HPJI3Up3cf3IYnw6eRKmLdyP3OLqgzuIJIawdvRGq44D8epH32Dae8MQ7GF2J9RN6ruFBZklqnEq5IWRiTnbIocOHYqffvqpot08ViZMmID//e9/mjx3EnHOyM82dYmcx5CIFjsV/UfUuHxckfQjNYSRiTls7Z3gaG8JA5KJikspqA8ReU5luVfw95yPMbhbBPz8W6LzgBfx1fyduFlE5VDevJsxmD3pLUyZtgwX83hlliPp6HJMeGEYxn+xBBfStUyPsvA05kx+B6++8QtO5tVsyy4ryiVHqXyYuvujVUt/OFqaUHAOKSSKEmQXkZkJRqCh90gkNze3Ku1kmzevUazVYWL95ptvaqRuzsgL8ssvv4yPPvpII2lVR8QtLS3Rr18/DBs2rErZD/uGmMYVy+BKkpS1o4cYOnkp8kkbdPboTvw5/TN8NW8v8u1aoXWEJ8xZGlemY+NX4zDqre+wfs9xnDl1FFtXz8EnE8di4qdzcYL4FQsrM6iKU3D8xCncyi2GWkFCxKJl2H1sJ+Z+uwTnCqk+RRkyr5xE7KlbKBXZwMKsJpIignXQMPy+ahEmDfTVEnG1AtlJRzF/xpeY+/dluPpHoUOoJ/SUBQ8b2or6586dizZt2lR817/gscWCCucZP368hhHU/70xruvNXrMUyDbwZ599VsOV1LSwsk2BF2XeG9gkEy24BrS4ioijZcmcJ4TGIY7U2DlZqeQAlIAtK37DH8uvwrbdOHQOcyR6r8StMzsw/cNPMH/TCWTLeaEU4eqFOGzd8DfGf/kjPhrRCi5evjAtW4aju48j/dlgmKZdxZ5tf2Pz9mtItwxB1/Yt0da9GBfi43E9tQC9HEkapwhH1SUDEwdEDXoZrfqz5KXC2Y1nsYCcQ1Tlba7umYd9r1evXppFkt8/S0Z3Jp4ILLUzN8vqKl5U2TGSOdzqFlV+nu2fM2bMeGiqrDv7UNN3MXGHNLRICiISzTSYkpqkj4KcbNy4egYxO9dg4byVyDALxogeEXAkNYwy/xKWfzsFX8zZisvp+aS5IUko8RJid63H6u1TsejnMXAyc4GzmxI7z+3FmWsvIahFAeJ3b8Pe7VuQcdYIbTq3gad9c8iuncCea+kwIq9lZ3Ne7qtPZh5t8donMzAcDvD3s9cQBlVJIhZP/xZbr5eiw4THEWpb8/PVl/pw7q5YsUKzHrFJ5s6kix/BvjspKSkYOHAgVq5ciTNnztzV7Mdbz1avXq3xYGfm7GGmL774Amwm0M2NYpKyVWQTT479Br0Dv0UhMcglZdqw01qNoiHcWnbHG5NeI/uzDWSFeUiK+Rnv/7gDEv/hmPPVG2jrTLbqy7FY+OMPWLfmd/zs7obXor3g7mSJbacTcOJiIuwzE7D+4HUUkq9HzvFl2Lj/P3CPVJN5KAGJcim6BnrARF5A2/RqIuaA1Jh21JQVIZ/aV5qbhJXfTsLHvxyBxC0E/Xv1RICdSrPNT4cw9zEiIkKjVXmYmDMtuJdZmMcI28+ZHq5atQrsD9RYY6V6alFLxHhSfPMNSYXkGMIOIndLHDhi9OjRms/d8jXWb15eXhpHPJYKNUlZiGLiaJXFl7Hws5FY/AkR8DxSXStvt8hAaoJWA17DB1NeQaBJCTKTrmLjX/OxLjYf7V/+Fu+MGwBvC1JJ7V2ML774gzxJp6FlwAz0p0Ea5WKGLce24vCZbvBMOUL+A4nIL87ApTNHcDD+HLzEJThO94okvmSPMkdZcQHyym7XXe2VWo6iYopERwu9nCZHAfUlT09saqxBVG3b7uMm78Fmpzj+3CsxB/zMM8/cK1uj/85e9Nx+7bhSo4A0Kwpisi5u/BI9tnyBoswc5LENpjyJJOZwC+iCMcTEPN3eASV5t3B68wLMX3sERsHDMX/ReHT2t0HJreP44/MpmLHkQ3wYEohvRrrDN9gXsoRL2HsoAa3FxYiJO4ukDNrvLIvHoYMn0NGfbNxHD+JGnhrNI5rDvDgf5aNdV32lvw7ewUTGKckKkJ5xGSu++xBfLIiFbedX8eGYKKgLqj7PmpIPP/wQixcvrlRWU//CBOLgwYOaT23bykJKTYJKbctoiHy87jJh4Q8nEanWJWI1ZCXpxJxQiNMKOqo1zagsfNBxwFD079QC1uT3A2Um9m/YgMtyD0x5fzL6h9mxEhL2jrb4j4rMBx//gJOH9uJG9NNoRbt0diScwclzSbAT7caZjCLY0Za2DNrhs2VrLIYG+uLy+XMQmTmgRWAzmJFJR9cuTePu8o/EyBpBbXqiU2wmYo5fwbo/ZpMJ4EOM6N4cxjpKTs8zo89ak0ch8bg6d+4cHn/8cY32p767dGrb54pXXtsH9PPx5H333XfvScT1n2m61+WqdbGK1OZyqCVmGrUnS36ODvawtTaHmXUQeg15Cm29LWngk7039RKOnTwH88DOGDliAFq625E6yhmRg8Zg4n86wzTnEDbuuQyRaRA6dXdDSXo89pEN/NKpeJzNlNPEcUTJjSQkHL+ApGtXcDo1D8bNAsj73ArSR0P4abqvs4m0TEz2bY1bEIWcLFOKYEy2Nh5TTo4OsLO1pn2p5gjs2A/9uwTBkrYFKQtTEH8wATdl3nh8xHB0Dm0GKwtLOPt1xYSPJ6Gnuxr7lm7GNaUJ/MNbw0NUhPMxRxBHGqOzV5IgsXOAtSgbJxJO4EZaEs4Roc9XWCIyzI/ace/E2oKsxEP46eO3MXVJHBzav4wfvnsNLW1r8/S9yxdyPAAESEMgFkvhHvEK/tp9kFThp3H23BkcO7gDC2e8hV7epdixbAE2xpCNXE5cvyoNV05kQW0RhVZBVhoirmmVyITMh83h62WD/MxU3CowRVBUMOzNc3D88EZsIh+OPJEHXnjrDfTxtMHZbZsQe+k8zp7JhYm9P1qS89rdCIpSRg6e2XkoVWhVUwbGlogY+Dp+p91Nsz97Cja5p7Bp/Q5cobXxUU4cL76xTcj1mp0sZfNeTd6z+U9ILMGKTVzRf/irGDuiK7wcLMiDWIa8jCQc370cs2avwLzp3yM06Gv08ZGiKC8DmbkK2Pl4wt2RQrzqQBCZwT80DJaG22mrVBLKRBEI69gFjovnYe+mjciTJkDpEIyB0S2Qsmc7Lp6MxSFzBZIyS+DeMQAe1qa3y9KVWe1f5srZP5UTsbB6XGy12YWbjY8AO53R/+5dXsTnk4YjxJM8dckIWJqfiUsn9mHJH79hx5bfMbdlC7z3TCSMCnNpv3ke5DbuZIaypz2/upcqgqkHmWCaW+Pw5bNIzpbQdShCvaXYc3YLNqrMkZhhjU79u0GaehhHzp5A/AlnXIyn7VI2EWgVaHPP4aGUFeLG6V34Y+YsrI3LQFCf1/Hhu6MQ4c4Oev/MxHEk2H+DNSh3k7Z5ceYARJz3YQf7YSmPHdp0Tm0GtJ2RPDEgMaatjL7ecNMZmSkgjLu3F2wNS/D+l2uwc3ccekb5wdLWGGbm5JBWRrHMs+QQOZJJkV8v2axltGUtv0hBDrTmsDC1hE9wFIKcN2HjrtW4VFoAqdcLiB7QD95nl2Hvsl1Y/Zcc126SUBIdheauFHBG52RZZbiokXxkDt6ecQqPTZmOZ1rblq9xYpjaNEN4+3YI3LwblzJvIrdQAbGT9iQ3XpM5UiUHH3qYibUMrDFkx0nWiNSU2JeCnXdZU92Y22LrRch5mwYPppkzZ4K3GN0t8UlJHOCfHZ+agsqXbfbcjopJKZaQcw9NDgMpOZO5UFs94GiqXb44oIJXQAtYFN/Aa7MPYN2m0+j6emsY8V5gKYWozMumwVcGsYuRdkKoSpFNTE4ZBZRxcbCBEam7XcI6oX2zv7Bs/xqkmgJu4d0xoH9XHE07heWn92Ndrhw38o3QP8gP9pamkNzWj9UIK01djTczt5Ins0RC3s1k49eltm3b6i4f+l+ds5HOe726BvH7YO9QjjPA9su7JR5PXl5emn2dTWE86drKe0t5Tujeg5TeCXULUnNbNKP2ujmVOyZa25KNuxlcrFW4NeF7HNxMDF3fMETQmDI3MYSKtjzmkoORkqzVrA3lVJqdjtT8MhhaOGuidFkbBSAi0hcb58Ria7IYxi5RaNtnAFwv5uLMXHJeWkFj6no+nClqVpCraUWbtKVV/lctz8Olo+sw+/s52HdZiY5Pv4sJ455AIHnZ17g2UxHcV34PTWmscc/YXsnxBu5GnJkot2jRAv3799fYNtkn486dNjqUmHjyrgr24wgNDX2osTDYns/jX0copEWmmq1hIhHFJzAlAmx2ew0glzVEdeuFiBW7se3ESVzPHYww7+aI7Ep+O/uPYP26Q+jo1gVOFiRF5lzH0X07ceyaDN79o9CS1OrOpq3QJaIZdp28iMQcNTo/1wGhzVrAf1gffL18BrauWgdDKw8804UIuZ3lXbaN0SmAihxcTtiBBUt2oXvgk7QVk9Y5cv8tyL6BC4R9YhrgGEB2eWdbohNaz0qeR7yzRddX3fto7L+8k4F3Y/HOhurU/DwPOC5G9+7dNf5Afn5+jUrn6kXIGcz//ve/GqmcHTDuNnF4Ijz55JMYO3asxuHtYS++PGF5L2CFDYNUiia075S91Q2I8JpSsA7zSsFVzNH5ySFouTAOp/ZTpKdx3eDdzB/+3g44FJuA/aQO9XeIhJ0x7ZdMPIzlq3YjR+qDseR1bGNhDrl7a3Tr5oNlxw8gx6A52gZ1QLt2kZCeCsbmmJU4cLEI5t6D0IpUoA62ljDVn4s1jVrymDeiLSa80EqNOGiNObX5tmsx79luComxZs905lI5qAYT9TsTE29eVHkvpp2dnWbS8PupaSFmzpc9iHkfuouLy53FPbTvrJ3iia4dV2S3NGUphbYHkerT2MSUJCF96daMbNfd0bPdEvwcdwwnrhSgUzdPhLb0guW+Aziw9yDatHBGMPlXyAtSEbPsL2y/WoIWT/dDK29r2JCqvhUxax5LDuJIGl23C0B4eBsEuF7G8g0xOECYF6pt8XTHNvC2tYK5Zn9xddAokX5mF5bOmY8DSVL0HfMe3hzVFz72ZtR2kvX4U91jdK+goACvvPIK+YR8UUOOxr/Nwah40eVdENWNH34f7NnerVs3jfd6eHi4hphPnTpVs++ctz3emdgHiIMRMWH5/PPPNXuH78zz0L4zp6h5QyQpatVzlZpi4R6MjmGe2LH8NE6cT0WvEFe0GfQMuq08jZ2/fYz3MvogjHa+5Fw/gf0HjqHUpQf6DSBfHhtmQl0Q0SkUDhtikUQMQ6swClpkKIV91AB0912IOadzifkOQbe2fnch4twcMbzbP4nHWm3F3LXf4iPpVbQLpCNK1SVIvngc+/YdQbZNazzVvzu87KvfvlapU438hcP08vpVXWImgwn3qFGj8Pzzzz+UEL71JuQ8sHnrEEva7EUcT57XFQ5ker1mSYyDxLAqfty4cU0qfKi2mdoFi3XV7AFeXbL0bofuFN1qdsJBHLuYj5Bwf3SN7oE9sYuw+tdpuH48HC7k7HbjNDmwnStEq8fHY1CUs2aKSQytEdahC3z+jEOalQ0CI/xJ8nZEUGQ4mrttx7kUBZpTCMgQCtagk8Cqa0Ple+z0wh+WyLXhMiv/3jS+8bafhQsXaoJ0VNciVlly9C3W8LDUww5UbEdmTQ9LSdWNJ97T+fXXX2u4YCbmD5sxrK5ffI9JoGadpZdUdVSJYGLlhoi2UTDZsw/xx84jr3sPtOreE+33HcOGTb/j81snEEz2yNK0C9i38wjEfn0wdnQ3OFDQDZEBRcIKCEd4gB3i81VwJcbS09karnZtEOnnhtgLN2BmH4Ye7f1IK3QXzlBdipSL8Ui4mAyYh0FScAkbFidpiAI7UhkQk2hpYQUrG2eNXT7I42FHNawJbe39vXv3asZGdbl0iy7vsuEPS1GcIiMjNUGHWOLisNIcjZC3QOonZkDZnKiLg6D/28O8NjC0gourPZxd7GjtqMpyiYydEN4hHB7bNyIzI4d8gEjybfk4pkwmRvmHNUjYNB+7igBre2f4hvTB4yNfxhMdfcodzozhHdoZrZrvQL5NADEE7jCktUZiF4aBT4ZjW/pZBHQYgChf2mR+j2To2Abjp0xA/ncUPXPnIuxdmo1SNdnlnV1I49kNY4e/iKd7tIRlEwzRWtP6wvSsXbt2GiduDj/+sDQH9Sbk/O44glLfvn01khFv/eC9mryNiIm3fmLJjBf12no16j/7wK9FUljaO8LN0wNOJBFX52wmMXZH2+5RWHr6EjJy8sme7oWIXk9hTFYhFq7cjoN/L0OZ2ATOzXwRPXwUxox9Es2ttbYescQIbiEd0K3VBhw1bIOO4XSOsJjuBbZB+8gQnM3OQGfaMsR2+Qpb+z07LSZC4ESLEatsbUnNX/sn71l0A2ZgCUinar6zWLYnsYcnM3fe3t6an/kEt0GDBmnGE28T4oWVg3zwIqqfeDyxzYrHU00TTT9/419TiF8zWwqi4g4lLbQm1bwfiZE5fMJaI6LZcRRn56BIaYBmIT3x4ssZUMxfhf1xmxG/VwRLB3f4tX8KQ17+Lx4P13oZkx4GNi4BiGrfCkfyitGqTQRcLA1oj64/qfhaY3vCLYjb9EFbP1vyar5L70WGcPCkgyvC/XBpWywW/HiImFk6e5zeg4mRFAakLTGmOW5s7olh706Hv3tQeQCau5T5EH+qKQQ0a3o4muALL7wA3hLJwod+YtMfb5FkAr5161bs2rVLsyeY4xXwusWJF27+NKVkYO6PoRRzoa1FezhXBBPSb6ERfNo+gdGvkL2chA9zzkOBr1oNnYjvvdti/+HjuJJBtuiAELQmprKFlyOM9SiDuUdrvPDKq+gg9kcXYhq1Y8kSnUdMwmTTE3Dv3gtuNUUa0m+GyAjNu4zCV15ROHLkGE6fv4wc0hgFtiRfj9AQ+Hs5PcQ48PoNrXrNWhv9xGOMY61zpMARI0YgODi4xjVO/7kHda33uupXBXeMg8mHhISAw9nxJOAFmMNo8ke3PY0X7poW9fq1oJ5Pi0xpsA/EOLO2cPANJEe1qiufWGKCsD5j8a70CvyC7UnWEsPCuQUGjZqEgMhuOE6nDxXTBPEKJFtnaCBcbExu2xdJsrH2aIOX3v8I0UpfdPLVeouaOJI6+cXX4NZZjqC2rWBXyb51jz7RAuwe2g+vTAyCtV+IdmvJPR55GD+z3fvO+AFsn+S4+yNHjtQQbf6un5g55EWXD6pgIs7jiRlEHktswtFJ6ayOb5pEXNsbE9cwPP/aJBRa03iwrOZgFLExXAK70/YzU+RRlDY7GndiiT0i+74Ae59I9DmegKRcERwoUEtE63AEeNBCqid0GVs3Q4+n34B9m2IEROmkGRtEDHgBE40iYdqiE3xsqqlXH2xiCFxb9sTYiWQzbncSGUW0pZHU9iZkvrAwNSIrPe3kkBWjuMQQIf72t8d0pTKazhdeh/QTO7R5eXlpTDEcSpPjrt8+LEk/p/aanas4lgEzmDze+IAeHoNsMmGpq6kRcrHUAR2HvFS1IxV3RDBzicAzY4gYkXpIN3xEYnP4RvXRfCqyVnMhMnJA+ydeQPtKv4lg598D496K1pRZ6ae7fSE7vq1nGPrx5275mthvrDrn46553WH/qs6dO+Ppp59GdHR0k4hl0WCEXIc7excy98ILLEvkbOdk5wxefDnx4sweoE0vGcDGPQy93O/SMtpKZOvdBsNfooWiYkKQ16W1K8I78+cuz9L0kVIwl1Y9hqKVXjaRxIImUl/66N2s9aWIGIlg9B4UXOsnHkZGthfzgTn8l9WTHCiBbeHsM8Hj5G6LKkvnrPbkeOwsFXFAGdb28LhiSZ/VWk2ZkBuYuqBdr4F3gZ3Gj603ug7wItV7uRqecosNLeHdsoPmc5eHKeY1Of2R6tMrVD8XhYR1b4UhL0TUGhuuzyeih+ajX9KjeM1Em5lH9sdgKZwXW445wIsvm3Fqk3hMabYJkomHD15hXwDWADHD+bDUp7Vp993yPJB5Qjj9GxI7F7766qsaz3UOUMPOnSyUNpX0wCgqS1SsquIPTyCdBMXnuT6QAdWIiD7q7W9EqCqqYhs4h/Dl98+MXlhYWLVhWyseuOOCxxNLSvzRjScm5Mwl/yNSBWPYcL35N49Tjm/BtmwdE1ifRZfHGRPwO7VGDfem6lYSaz85yhgzuf/0d9xU+soCKoeM5lRbZrBub7V+uR8YIddvFqvSm1rneXKyJMgb9x/2HkV9rBrqmqUGliCaivTAEjXblBjr+uLN740lrqaW+AAX/txNw9DU2lyf9rBHeFPtLztActv+MYye3oti2z5vr+OdG03STKnX1vpc6sYXr9UPOzHD1NRomD4mDx8h/dY04jUPDpbydJqCRqz6gVfF6msOFdiUTBjMWbM0Xl8i/sDBq0cFPKZ4wjP2dwsaUY8qmtSjLBVyX5viO2Ui908k4jwAmKAwk86nbjV2BLHGGoDsj8B7t3mN/jdoHuqL67+WkLPUxKoy3vfLtnzm3v8JidWJHLSfHXKYeAqp8RBgIs7SEksS7Plc3YltjdeaB1cT7xJgBpiD9uj6/OBqE0q+EwGe16zd4vfAcb2Z4FW39/3O55r6d16D2Sma/WDYB4bXaPatEdaxe7+5RlGt37sZjZ+DFyCWEFmK4gWJT99iDp4/zAE+SokJBxNw7gNLSTz42bNSSI2PAJsy3N3dNWcXs8czE3Z2uGJHv6agIqwPIqxl4C2ATMR1e/15nP2T1bv1wetBPsuSqhc59bHkqpv7zMA/yonHEc8X1qbwuGIHs0d9zjTW+/jXEnIGmIm5zguVFyeeFBwI4lGTpJhzZQaEVW78lye5kB4eAswI8iLLns4cn5lVoDy2HnV1Oy+qrOnhhbYpxL9+eG+4adSs04Yw8RPSvxuBfzUh1716JoTsPNUUHah0bRT+PloIMNHTeTqzhkRIAgICAgICDwqBf62N/EEBKpQrICAgICAgICAg0JgICIS8MdEW6hIQEBAQEBAQEBBoYAQEQt7AgArFCQgICAgICAgICDQmAgIhb0y0hboEBAQEBAQEBAQEGhgBgZA3MKBCcQICAgICAgICAgKNiYBAyBsTbaEuAQEBAQEBAQEBgQZGQCDkDQyoUJyAgICAgICAgIBAYyIgEPLGRFuoS0BAQEBAQEBAQKCBERAIeQMDKhQnICAgICAgICAg0JgICIS8MdEW6hIQEBAQEBAQEBBoYAQEQt7AgArFCQgICAgICAgICDQmAgIhb0y0hboEBAQEBAQEBAQEGhgBgZA3MKBCcQICAgICAgICAgKNiYBAyBsTbaEuAQEBAQEBAQEBgQZGQCDkDQyoUJyAgICAgICAgIBAYyIgEPLGRFuoS0BAQEBAQEBAQKCBERAIeQMDKhQnICAgICAgICAg0JgICIS8MdEW6hIQEBAQEBAQEBBoYAQEQt7AgArFCQgICAgICAgICDQmAgIhb0y0hboEBAQEBAQEBAQEGhgBgZA3MKBCcQICAgICAgICAgKNiYBAyBsTbaEuAQEBAQEBAQEBgQZGQCDkDQyoUJyAgICAgICAgIBAYyIgeRCVqeRFuHnlNGIPH0LskaM4f0sOV/9IdO3ZG9HtW8LeXApRXSpW5+HgX7Ox8rI3xk8cCl9Lw7o8/ZDyqnDjyFx89v0hhDz/Hsb09YVRDZ1Wl6UjZu1CbDhrikHPDkFbX0dIa8hbXWdUZanYtehP7C8NxYsjesLT1qRu+FZXqHBPQEBAQEBAQOCRQKCBCbkapblJ2LVsNr79eSVO3siHXFaKUpkahrt3YMW8X9H+6ffw9UfPIdDepPYAKdMQu2oNlpzyR/dnBz4yhDzp+Eas2boLa2JvwXjBHPynoxOqqEBUhTixdQG++uZnHExvAbe23RDu7QCppPaUXC0vRPKl87got0ehTAk1IVv7p2v/GoScAgICAgICAgJND4EGJeSyvCRs+XMqPv5mNXKsQ/DMxJfwRK9INLMxQNrlI/jrp++xdOEUjJcbYuGM5+FmXIWs1YCQCvISGcpKSyBTMpl6FJIYRsZmECtKkX5tGz55/QM4Lf4OgwIsbxNZdRmux67FzO/nYn98Igrs/KBS171/BmbN8ewnv+JpSGBsZFiVWXgU4BLaKCAgICAgICBwXwg0GCFXyfJxZu9izPxlK9Qtnsa306bgsSi3CnVyc99AtG7dEi6vv4zpf32BpSMGY2KXcqJGxEupkkMuZ2nSgKRRMcQGBhCLdHKlCGLSNYtEKqiU5f1Uq+gZNURizne772q6r9LcpzLo+Yrvmms1/aaicqi88vJ1v/N9MZdFhfHvmlRRh5iILz9b9fnbNVe9MrOwhZFYAgc3O8jPL8fkiS5w/P0DtHU1pvJUyEs8gvk//YYtp1IhNjWFsaZ+qkuvP/rt0LVRRG28jQ3lEIkhMTSCWE1t128G46qQQyaXgzJAyuUb6D9LvytVXADVqYaaMKAuUh4JDPRB1S9TuBYQEBAQEBAQaFII1FYkvkej1SjMvIwtq9bimmEQnn/zTTze5jYR1z4sgqF9JCZ9vxgrls3D8EhzDdFRKUqQfGY7po0fjFAfd7i4+6LTwJfw9fztuJRWAK0ALoaB1IiKURLhoT9qJa4f+BlDej6J77ZeJZJYntRFOLfjF4x78TXMXhOPPFkhji//CEOHjcOX30/D6yP7I8LfF+36j8b3Sw/gatJ5bP/ra4wZ0gNRka3R77n3sHTPOeSVaSpBxonFeGHQYExdtAeHNvyKN0f2RUQLf3R6fCy+XbAbKYVyjRpbV/2dfzXEFcYIffFrfDWuHbJjf8MHn8zBmYwSlORexdal87BqfxpaDXwOw7uFwoGM6JWJuJo0EVk4tul3THhuANq36YxhYybj9+V7cC2rREN0NXUqbmHz929gyEtfISYxh1CipCpF4tGlmPhMd/i7O8C1WTB6P/U6fl1zEDdyyjSYydLiMXPSf/D8q+/gs8mvYXCvdmju0RIjp+1EHlN0IQkICAgICAgINHkEGkYiV8uQc/M0jh/PgmvAYPRs74Pq3dFEMHFsgd79ynEhgpyVeADfT34L8w5mwMLKBg5matwiwj5jynEknJuEKW88hSBHlsjpGY20TX/oueTT5Eh39iTsb+RpiJKGI1GXIu3KBZw8fBjilgNRWOqKayeO4cje3Vj3txEcHW1gZixFwZnNmDbxINYGOuLmufMolprBiJC4tW0upmUWwvh/H2BgpAuyE08gLn4/Nh07jNllKhhamsPYUIyChL8x8/xJ5Ih/xQfPRMCMpNzqkoGEG10KpcQVQ9+Zhlvpr2LWppn4n50xhrRIxdyVeyFp0R+j//Mkbiw4j80nSSrWYw3khTex5Zf38c70jciRWsDMSIyMrfNxeOffOPLSp/hk4hNoZm5AWoocXIpLwNEDybg4ZiTaNLNA9unlmPifd7En3QDWtm6whwKXj6zCFyeP4OSYD/DumP6wzUnC0WNHsS7mPAys7WBN/TOysISxlJwRBTpe3SsV7gkICAgICDQ5BBpEIlcrFSjKTMWtIsDO3QdONrXjD5Skjo9bNwerE4rRffRX+DsmHifiY7Fp8TcYHG6MQ+uXYGPMOeSTZtiAiKWICLhWQlejIC8LarEZ1WV+2yZMKmaxhNXjaigUCpJYWeXMqmojeIQ/gS8XbEHc8WNYPfMluMpTEH/yJjy6jMHMReuwfesyfPRcR5ReTsDh45dJKlcRw8Dvi5XgpogYMhF/rtmJ2LjDWPXTGwg0yMCeddtwKUdR40s1IPU9P68kNYKxQyheeu8DDA4xxL4/P8HkqQtwQeaPwc+/gG4hzuVe6kTGywmoWp6LuJVf4/2vNkESNhxfL9iImMMxWPnrB+joUoIzR/bh8q0yDdkXGxjCxFBCqnVyLCRtgrLsBlbN+B57Um3x7EcLcCD+FBLiDmDVb++ji1shdq9aiM2HE1FWLnUbWruh+zPvY+nmA0g4GYs/3+4KyxqYkxo7K/wgICAgICAgIPBQEGgQQs76YLY5S8mGLSsjhzT5XcQ5VRnyc/PB2mt5yXXEbD8GOLbDc6OeRLCLBUzN7RDUcRBeeKYXmhlcw7FjZ5GRryACTVIv23E1RatRVkJcg8gAZiZGGhW9Fj0REXwi3GKytZO9V62mNkmpiyJLDB73Fp7pGggbCwt4R7ZHmIM1nP17Y+Kn72BI13D4+gUhPMKX1NuZuHUzHUWlauoT28YN0eKxyfjj+7fRJ9IHdiS5eod1QGSAEXJTTiMpTUtMq3975ZI6t1kkhYNfNMZPGod2nhLkFRujw6CReKp3KKw09n/OSxnL+5dzaRO+mr4CmS59MOWrT/BsdEs4OzjDt0UoArxtUFyYi/ScgvJuS0mSNia7eSnKyGu99CZJ2TsSYRv5HMY/3xWu9JuZtStaRQ/Gs0OjYZ6diGNx55FNDBI1DLYtB2HsmOFoE+gKcxNylqtewaCtS/hXQEBAQEBAQKBJIdAghFxEem9LVx/4OInJO/04zicV6imI9furRuaFHZj97WzsvEC2XHkm0m6UEBHygbuj3nY0sTmcPdxhayZGVmYWSsoU7M9FSUPl6K8IEikr75UoLpVV3OUcOqquzUmEnRgAYjNgZkaETpOBpHtDU5hZGEFqZAX7ConeAEamdE8sg6y0FAoyvOsc6azdPOFirtMyiOg5C1jYSiFXFKGopKy81Kp/1OXiNTunMW0Ukwrft91QTHj3LYwf/TLGjOoPH1vuh9Y2Xk7KiQEpw9kdq7H/mho9R7+Jx8IcyttO/TYyhwWpv0tK8pGZX1Ted/JWN+W9+WUoIw5JnpWGa7klsPX1gxNhqEsGxhZwcneFrVEpcrOzUExNZ6c5QzMLmJuSRC8QcB1Uwl8BAQEBAYFHBoHbq3x9miySwNopGO07BaA4MQYbNx/BrcJqVM6KbBxe8StmzP4TBy4VkUBtCRt7KUpyLuBKckGF05pKlocb15KRVSSGnb09TI0M2DxOidXmRPZIEnfx9IUJ7cG+fI62bSm0ZFslK0ZuTj4Rd/ZAZ+JIqnZ+gEpmj28dcdcQTi6H7Ma3fbrII508uNVUtgGr51nLQF7enBRaDzvNNf+j8XQnHT+Xz5+akrrcxV7bBm0uQ3MndBg8DlM+Go/O/rbUI0oVFLScoKtLkHYzFcVqM4SF+JI3u64G1kgoNe1UKIhok5e/1tFPQkwIEWLIiLlQwsDCBs7mxkg/QxqDPI3rm6YAeWEeUpKSka0wgY2DHcyNJdR+8sendmqc13XVCH8FBAQEBAQEBB4ZBCpIRP1aLIKxlTs69R+MVs4l5An+E35fuhWnrqYin/Z/89aywpybiN+1HPPXnYSkWQd0C7OHoUkzRBLxV6TFYcmfS7H/xEVcT7yIw9uWY96ynbgl8iRv8iA4WEqgkDEhloBoLFFgA3hEdEOEM3By+xrsOnED+QXZuHR8P3bsTcDNfNrERluoiEZVltZ1ndQQeLJ9E4FWVuxLJyJJVF3FzIKGkGsZBq2nvDbIivZx2rIlJ1t0kYK2aJFtmpznakpsGwekmu10+sIuE3+2n+vf0zZUu2UOYhO4+3jBUpSHfdu24WxyJjEnxUi/fhq7Nq7F7mPXtJ7pFQoKMiEYcnkyYjoo+I5LGHpFOSP71Er8Mnc94i8k4vrVM9izYQkWr4lBqa0vIlu1gD0Rf26D1gyhK6ym3gj3BQQEBAQEBASaIgI6fXG92yaWmsIrsh/GvHIDM35ahUXfTcGelR5kU7aAEdE6eUkB0hJJ8s53wVNvjkY7DyNIRHZo99iz6LZnKravmIHUk2tha6pG3q1E3Mg3RrvBw9CnvT/MpTchLyYJnyR/iabFIlh7dcLTQ9ri41/X44tJSVjiaIhceu7i+avIVbprCKVYTJK4RtRkwsn2bm1ilbmE9qqricG4LYnSPXIYk4gUZOcvg5x+kJA0Lya7v1KrDih/mgl5EQoLiWCaWGq84HXl3gmiUqUg+kzlarQCd/56+7uaCL6CmAiNNoDaKSbnvMAez+DJ9vFYuWgqXj+1FA4WUpTmZyDx0gVcvpYKy5ZBVDb/p59Y80A1mvli2Ksjsf38TKyc9QnObnaHuUEZ0lNIGi+1Qp/RQ9GzdTMY513RaB5YLVG5HP0yhWsBAQEBAQEBgaaMQIMRclZUG1k4kwPXyzC388amreThnXAW8QcOEvEwgB3Z0Fu0jMYbfYdg6MC25V7RUriF9sOE94thu2AV9h47j+QyUzRv2QYvjBqExwf0QCA5wBnAHO4tvOFT7AcXks45GZq5oMfICcgoNsSSTUdwJNkULdu2w6BAf5y9ooSHiy1MJLTlzNMfvv5ieLvQvvVyiisxskfzkObwKfSBrUm5UoKIp52rN7z8AmFNjnCG5LVt6uiFQD+SXL0dSW19m1yzbd3Nxx+BklA4W9cEoQhWzv4IbRmGEH9HvaerDgeRxAzOPp4ICLOEm50ZDEhit/LuhnemfQH3xauwbW8s9t2SwcnbD0GdByGydSpSZO5wp7ya1quJ+SglMwGMYKhx7jOCb7fR+PRTMf5YsgmxJ4+hSOqMFmHdMaz/IAzq2wVedkbE5NgjMMAP+RJPYqAM79rGqq0W7ggICAgICAgINAUEROSQpRHGRowYgaVLl6Jdu3Y4dOhQPdqmVT3nZ2ciPSMDGeSsVigX0x5xOzg6OcHZ2QHmtGn7NlmkrWJk285ISULyzQwUKQ1h7+QCN1cnWJOdV2s+liPr+kVy4DJDYFAzktC1xFdNEm9B5g1cu55C28UMyZHLDVaGpcjMKoOlkztcHcxQln0dl66XwNWPPNIttMSKg9CkUXmZCgc0b+4C0/K45rKCNFy9ng4Jbcdq5mwDsSwDFy+kwNDVD82dtAFsGBhFWQFuJZNtHg7w8nImhqF6uBRFabhwMQ2WXgHwsOGANjUktRzZKVdJC2EId0832JiVE1Ui0AUZKUhMSkFmgRIWNnZwsLeBRFGI3GIRnJp5ag6ggeI65r0xFh9tLMXE3/7AKz3Irk5tUpaRr0FiIlLSMiEjfwRHOPenygAAQABJREFUZ1fC1RGWJtpDa9SkWUhJvI48kTW8mjnBjNTzQhIQEBAQEBAQaHwE2rdvj8MUA2X48OFYsmRJnRpQAwmqUxl3ZCZPcSk5Uzl5aD4Bd/xa9St5YhuawcW7heZT9Xe+I4WdZzB9Kv8qovCnliQ1h9FHPxG9qkgS0g6E21V81VyIJSZwaR4Gl8q3YWjhhMCWTrfvShwRFOF4+3v5lYS81t19Q6rcv/OGxMwJwRF65d2ZQfedtqbZugfAVvdd95dMCRaOngihz53JreIG7alPvYYLSUSspb5wosNoNNvX6XcD0hx4BoTRpyJzpQsRedG707Y790p3hS8CAgICAgICAo8SAg3k7PYodfmf1FYlUo4txeTX3sa8A1fgERWJIBdLUs3/k/oo9EVAQEBAQEBA4G4IPACJ/G7VCb81LAK0XY23jpl6Y+Ar/8FocmILctaLdNewlQmlCQgICAgICAg0QQQahJBnZ2fjtddeq7Nevwni8VCb5O3tDUtLy/trw7mLOLr5l/t7lp5iVwneLieTyWBKJ7E1VNIFxalLebznX0hNFwFzc3MEBwfXuYFyOoWPP1ZWVrV+Vj8GQ20fMjMz08RHuFd+HmdltEMlNzcXJiYm5TEn7vVUw/7ObeA5V1hYCHuKmdFUEs9bflfFxcUabIyMjKo0jWNQMG51TW3atKnrI+D6uT5uU15enuad+fr63rUcQ0OKUnmPHUN3FsBjs6594rbxM9bW1pq1U0JbqypO0Lyzggf0vd6EnF/4zZs3ERcX94Ca2LDF1vXFcu38Yhoy6RM3/ReekpIC/jyspGuXfpt0beF97zwxGiNp99/from/84ffQ03vTxvX/vYztbm6s57aPKOfR7fYcd33U79+WXde8wJ/P+3jNukYoZqw0q+L8/K5BHVN7JTzT0r3s/jq5ktdcOB3WtfnqpuP96qT+1PX+crt0m8bjwv+zmO7prFUUlJyr6b8q35n5uLzzz/HE088oWE+GqvzDUKh+IXrBhtzNI6OVR3EGqtD+vUwp5uenq5pm7Ozs2ZA2tnd4fmm/0AN17a2tjUO5BoeqfE2T+TMzEzNx8HBoclgxZx3YmIixaaXws/Pr0r7ua11lcJ4TPCCUpfEhCUnJ6fiEV4oTp06hdTUVISHh8PTs6rjH2e+n/fKmiT9haui0lpecJv2798Pd3d3dOjQoZZP1S5bBu34YMmjLkknrVy7dk0jafJ7tKCzBe6WWBp90MwjY8zj69atW7CxsQHPp6aQeH3gucjti4igUwxJkq9L4rFZV2aroKAApRQCWpf4mvFnLZiLy53ut9pc90OUeQ0OCgrSVVOrv9wXfk+c+O+FCxc0Y5DnPc//OxOv+/Xb4XRniff+zpgzXiz9NhUNBr9Dbhe/28uXLyMriw70ojHVqIkq1CRyeeea1bT9THerVn9p4VXHx8ero6KiNM/37du3Vs81RibSEqgDAwPVoaGh6rS0tMao8p51EJFSf/zxx2qaaOqpU6feM39jZYiJiVG7urqqIyMjKdCbqrGqvWc9ycnJ6lGjRqk9PDzUCxcuvGf+xsywYcMGNanV1EOGDGnMau9a1/nz59U9evRQExFXHzx48K55G+tHWvDVc+fOVROTrx49enRjVXvPek6cOKEZ70Tw1BcvXrxn/geRYc+ePRpc6rruPoi26Jd59epV9eDBg9Vk7lNv3LhR/6eHer127VrNnBs6dOhDbYd+5aSdUn/11VfqgIAADQ38+uuv1cQI6Wep1TWPAabBTIvrmhrEa52lKCICjcqACJUJCAgICAgICAgIPGwEiICDmHk4UZwUTqzpY21FY6Z6E3LiHDRqhIZ0kGpMAIS6BAQEBAQEBAQEBBoKATZxMV1szFRvQq5r7L1scbp8wl8BAQEBAQEBAQGBfyoCbDN/JAk5N/q+t039U9+m0C8BAQEBAQEBgX8dAo8sIWfvT/YiFJKAgICAgICAgIDAvxkB3gnySNrIi4qKNK73/+aXJ/T9H4AA27Ua17T1DwBN6IKAgICAPgK0Q6rO2xL1n7+f67pt8q2hBpbIWZ3QEIlPIDt7bC+2bduP8xkKuAe2Q+++vdHa3wnG5aee6dejktHevbjNWL4+Dlbhj+OpQe3hZHYfpn9VCVKvnMS+7dvpONVrENl4o133fujdNQSO5pWP+FSW5ePCoXWYu3gzLtzMh4ycG5Tkuc/J2NYX/Z99GcN7hsHGpP6niakUBTh/cDs2b9+D04nFcA1pj+hePdEupBnMyk9tu42HCgUpp7Bz6zbsiolHjoEzgkJao2PnDmgVfPvUuNv57/NKXQZZ4hkU7d0J2bGrEFl6wLhDL5h3j4DYtOqQ4lPWZFdOoGj3bsjPpUFs5wOTrj1hGuUPMZ301pBJLStC6bmDKN65D4rEHBi4hcCkezRM6Nhase7I2koVUgSr5AQUbtsGWdxZOqOexll0X5h1awepU8NEuFPL81Fy8iBK9uyH/GQSxK7BMO4cDfOuran/1Y9VVWEqimP3oGTvJUh8QmAcFgwjP2/KL63U+np9oVP3cm5eRMyOrdh1+BwK6ZCgyM690Kt7a3jam1eO2a9WITflJHZu2ow9R04hQ2aHVl17oFd0JwR728OwAeP7q+S5OHtwJ7Zs24n4a6XwDGuPnn36oX2IO25PKSXSz+/DssXLsS8hCXmlcs0aZGhirtkPbm5hDe+Q7njq2cEIcTbWO22x7ogp6bTDpPNHsGPrDhw8kQyRrQ86RPdB7y6t6NhhUzpm+c6khqwwHbGbl2DDkQJEPT4SAzrSmK/+Vd/5cI3f1XTqYemZOBTvoXl0PpPGdiBMo/vDrF1zaM8zrulRBUpPb0fBmqMwinwM5tEhEBtXbXVNT9/zvloJRcZVFO3ZgbK488QM0zHQUV1h1iWK5hDFMagyNmjO3TiBwu3Uj4vXqe1OMIrqBLOOrSFxqHukuKrtoxM1My6haN9ulB08AhWdmilt1R5mPfrAOIDiiFRpD6AqTkfJcZqje2OgTKPgU80prkDvXpSfPNG1R3BWreaOOxzxkIPw8H5y3snVmKnqqnsftTeMYV+NkqxLWD/nW8yavwUXb+WjTKGG1Hg91mw6hClffIAnWnuATkDVS0S4Ms5j/fyZ+HHVFXh3ViAgPAS9Ai2re1d6z1W+VBOxPLt3Ob779lfsiL+G/GIZHR1miLUr1+DQG9Pw6SvRcKg4q1SFwswLWDvve/y59gIKKS/tuq54cRLjo8gwD0DHSH9Y06JSzZipXPndvimzsOPHyXjvhy1IyStASakKhtu2YPOWXRjz9hQ81zsQZhUnpKiQfmo1Pp08HZsTEpFTUAgFnbG+df1yzHVwRZfB4/DamKcQ7la3oBdVmqcuRtHBVcj/cTFU1zPpTFcasKI4yPdthezMZNhN6guR3hqhluURwV+Cgl+XQXWzgM5WJZFXdAgyXoxeeAtWw9o1GHFS07GtBX/PQuGvm6DOp3eoogktjoVsfwwUL74BiwGtaAHTfyMqlJ5cipxPf4cqtZDapqRF6DSKzsaidE9vWI17CSahzlUgqMsNtSIH+atnoWj+DqhzKNiGkiK2XTgPeczfVMfzsH1nFCT2lYmzMvcicufMQtmmOKiL5HQE7SYUS6QQu7eH9bvvUpvqHtSoSptVpbhxegdmTfsGK/adR25RCVR0Ct+GtRuw95kJmPLmMAS66OL20wl7idvxyevvYfWxFBSQBq6MjhvevXMT1q/rh/FvvYknOvnCVO+9V6mvljdUpSnY8MPH+OyPHbiRlYsiGvNGO7Zh49odePWzaRjV0wdG/ApVeTRn12PZklU4lkSqTH7XtOXHgHAyMJBAQoGNzHfvxS0LP8weE4VKr72WbeFsqrIcnNg+D9O++g0xF9JpvpfRYYzG2LJuFTYOGospbz+PCE+bO5geCkR1aQ/mfDsLG64Z4rKiGSLCPNHc8v4BUsuykL/udxQt2AJ1Jo1V6q8y/ihk27dC/vp0WA9uUS2B4j4ocy4gf9E8mqNXoEyyhEkEMbUudw8UxM/VKtFRy2VXY5D73XdQnEgF5DSHaNWTH9oL2fFnYD1+OAyb6YedVqH4yBzkfj4f6mzCkuYDcyHy/TtQun8wrP/7PIy86tc2efIBZE//HoqEZBARoTktgpLmdNnGv2H+6sewHOBfCStlziXkLfwRpRtjad2gNtESpTgag7Idh2D96ScwbVW7AGccTIuj4DERbxiaWKs3oMlUTx6x9hXdK6eaJkz89qX4+fe1iL2QhGyVBCYkrciLUok7X4mfFmzDzQLyBtQrSF6ciWNbl2HlptNIy8pHbk42EWF6EXVKSmRcisH8X3/Fmt0JSL5VDCkRYANFGZ1ZfhJLZv6ArWdz9Oql6Ed5ybh8JhWFMIZHYCt07toV3bt313y6de+Px3q0hrNl/aQAmqlI3DUb705fgZNXk5FTWAJzK3OoM27idOxOLF9M92/c1oIock5gzrTvsPoA9aHIHFF9h+PpQZ3gYlSEy2fjsW7RbPzx9ykU14tRJEkj8TAKFy6F6sotQEaThCO30cEtKCXGa91MFB/L10NfjrLLB1Awj4g+LbaQ09ujo2dJ7AUKk1G8ZDnKrmRrJo7eQ/d3SVJB2YXNKPx5PS0QFDaSGQYJDW+SOtXpZ1C8fj1k16guvaRIj0HOR7OgSqa2KagPBsaAIT1Tmgdlwi4UbjoOUtTUI6mJUfgbRX9tp8WXmBhjJ0jatKdFlCT9kkJavP5Ezk/0GzGsuqSWZaBgwwJaVA7TokLvl5kLGY3p4kKoLu2k9tIClcmLZX0SEeb0i1jz+wzM3XAIiTdzIZKYwkisRvaNc/h70Vysi7mMQll5u5S3sPqbTzB3xxlkl5iiZZfH8VjPcFghC7E7l+HH2XNw8EIWjdh6JtL0nN44C5/+tB4nL19HerYItg42kGem4tzJvZj74yKcSpdrKxGZwSeiA7r16IpOnTqic+cuiI7ugW5dOyPU24LgykdefiFKqA/3v8gpkJF4BIt++R2bjiRDbeaJLv0GoUuoG5QF17F10beYPncHUnnxr0gUxS7rKjYtWoitJ64jm6Sz3KxsFJc3uyJbnS4UKIlbR+Pob6jTKNofjxcpabJUVGhxCop++gGylBrGhLoIRQfWQUFaRiayqvQMYk5qyFunNnFmYibyU5C/8Aco4sqJJnPxLMESUy3fv5aY+DNQld4e34r0/cj9bA71o4geJ21GQDjEzWxojNPe60NrULB8N5SFt/PXtUnqshvI+2uutr9lIoi9wiGJpHOcDWRQZ5HW6YfPUZxwO2IiM9qFO5aidF0M1Lk02dU0Wljzq6T8aYeR/8tG0NJSq8RRTesaFrdWBdci0/2P8VoUXpcsxTk3cDRmP05eK4Nvu5H4ZckuHI/dgf+N6gVX02Kci0lAYgUhJ+k95yzmffIKxr77C+JS8jWElkKS0Xpcx+VEWYBrJ2NxNPYqlHYt8Z+pc7A7Ng67Fr2LNqQyLEyOw5ETNzV0QdMfeqsl+VnITCuFlZMvhk3+ERRtqOKzevkcTBrWHg7mlVQHdYFCm1eZjn2raEEj1b1NwFD8tCkBcYe2YebHw+Euycf1q2dxLpnCS2pyE9E/shHrjl5FtjgE7/60DCtIopv16yKsXvENBrlZQF5KKmdZLUdkTa0labzszGEoL6cRR2sDoyHvw2HpBlh/9zI04pgsHaWkatclNZk9yk7FQnWViJiJI4xfmArHVWtgPrEfSJUA5J6C7CqFSa1ns7g+NTFeJYe30WQk5sLUHWYTf4HjysUwea4rEWfSmCRegYzObK/gyNSlKFj7K2kJiFiKDGE4iPqyYh3s582C0RMdYODvD6NwH5Lgdb25v79qGUnhpRTC2LkzbL77GQ5ffwPHuQtgNKg5LchkojiwAmWJuuARzCjFo3T7YWJ06Bn7YJiMmQCz11+BpK0X9xLqm1tRsPXS/TVG9xQRzMykeOwnwlxk4o4B47/BpsNHsXfVlxjU1gfyW+dw8vQVFJToqI8SRfnFUJg0x0vTFmPNkj8wZ95C/Pr1a+jgCZyNPYJ9sZdRwMxTPZJKnoS9q/chOTMHtiEjsfhQHI7F7sfcz56EDTFXaVcO4cw17VwHaZs8Wj+JD2fMx5p1G7B+/TqsW7cWa5Z9i8EBRBhIKjSxaIHeHQMh1VfC1Kl9RKgUMhQVKeDUsjemzF6ERfPmYPHyvzDtlZ5wMc7B7jU7cYq0h9o3SIzQ+b8x5eWRmPzzdtwq5YGtIglNoeHH6lS1fmZFBkoOkrTIxM/Eh8b2TDitXgfzN6O1kmVBAsrOV2ZStY9rGe/itXuhztO+S3URjUeN1Kxfwf1ek3Yp8yRJ+omaOWTQdhTsF66BzYy3IPakg3FoPZBfuAQVaZW0iaTxfStIGCHGx9ATlp/NheNPs2D//Tcw7EeH8ChzID91GPIUWi/uO1Es+xLqI8xoffoA9rO+h8N3v8N29kSILETEHJ9H0fbjFeuAMicJZUdPQV2ghMi1LSxp/Xda9RcMe3tQn+j9nzsKRXbtFqia4tHfd1fq8GA9qQ31leJp89YzjjV7/4kIc1EmUm4lId/cEdFRfRDdIQhO4iswlBjQlKQFTL9wkuiu75mPz2ZsQAoRbjrMk/6jCUMUQVnHxURJNtXMW6nILJTDMTQC0b27oIWHHRIvEMdLfdOoSOivbi1Qk4RUkkOEnLhatagEScf3YIM0Df4tQxHo7QIzI25v/ZNamYoLxzJITS2Bf8/heLJrACwKr8OYJUZqD4/EilYRgb1x5TwyaZI6BvfCY9GBsDQ31WBiaUOn+fAJQKReEmuwrEfbVCRFXr9F6l4a9I4tYNKjPQzd7aFM11MNa9qmrUMtK4Hi5i0iWFS3B9nzuneC1IVOBjKi/BUgVVzUo2H0qKqMbOJXqFw64MG1E8z7RMLAhOLsGxLDwImq0WsaLS5nULKOCCINLLHvcNi++QTZ9wlRkR2M3m9bObO2hPv4VwTTti9AOr8flW0HAwuy/9HioDZyhNTPA2U0vlFK2p5iJgOEiTIPpfFko7tOi7IBtePx0bAe2VXTLuXAFkh7eiKp58kWvJMW9eGBlUwYdWmcWiFH/q0buJFTCmuXUHQe0BetmzvjVrYxxAyXZrLxeyl/NwbuePmnreibAbh5OpPSghgjhQ1cPZrBlWzEsZklyGdCX2mS1qVF2rzK3FRcJu2AXGGGyIEjMIRsvwalWTCmOaUtWgyRnr1SRNodIzJ53T6Xi9aFmDWYvyeF8kkQ/NhY9Au10PWi7g2id+Laoh+mr4xCgdwYjk7WkFBLlBIXeNNctzIxREpuPgqJUdPG/yjGjj8/xffrEjTjh9dGXj9USgWtTSxglI/FOrZEWZRDdlsaE1SEQWB7mHYKJVsynQZWYefWe1d6ZatovShYtYyIEb043bspLdZK5Py9/PXqPVK3Sxac0pKIcFJhxnYw6dMfRr7O5KtAb6TC5KcvKyohv3pO0xaRQ3fyEfEmTRA1Q+oCqXczyERnSVNF9uVi1jRa1q0t5blFRs1g984sKMaQQs6Ozsgw4rVPTXxDMPk20DgiaV+dq2MU6F3mkSYpi852IGZeGt4ZJq2DYWCeTtPxNji6c0Rq2yA+46CxJfN6E3LuXP1PfhLByjkIg4a/CgO/EnR4ogsc1ElY98t0zF4di7RiC/To3R5+1nTUIFcoEsMlvDdGjbyA65aRCDA+j3m/r+Nf6pwMaACGRT+Jl7KJi/ftiY6+lrh+eDE+IbvpuZQsWPkPQfco99v+DkTIC7OzkE4TIjP9FJZ89w6W0kAR23ih66BRmEQ2ni4hHjDTEZA6t0j7gEjqT9L+WKRuzMNjL3eDeXEq9q2chem/bMINlR26B7RBmI+Ddi6KjGHv4gprY0OcvRaLvUcuw6cL2RLFCuSQdFNEbWaib0A2HL11sO4tI+JiGv04VAW2kDTrSpPWhpxv1iD3f/NoAhLXauQD0w5+FeWKTW0p/xOU3wnSoP5kKxOhcPdCFM7ZBmoUSalRMGphf98EqaIiuhBJycnp8bEk3Z+GSc8naQJnoWDzApSs2E+SAfW9RRCkPk6UUfuULJG48BwmoEQcjG4gY8JQsl2nQuQQCKOufWDWtwf1z5HadntC69dX62uSHKUuHprsisxjZLv7EYrTl0jdT3ZOGsdiGnOG3lqxX1WcDfmlZCLuxKQ5B8A40pcc9LT1G1gGQhJmDvmePNIunCPVrgoSa/1FstYtIqxM4RnZF6P/m4frpm3weJQz0k5vwcyvZ2PfyWtko+yBtlGBsNJzXJRaOMOHTJdycgrau/oHzPhjK05euIJEMkU179AFEeFesKjifFn7NnFOqV0Inh77POQhMjz+LJkgyL/i0NLP8MH0Dcg1t0VASE9E+FrpXmGVwhUFp7H49zW4TvZ+M9feGDe2Hxzq2SaIpbC0cyGyokb+jTgsnfsHlq3fS6r/ZGTmihH1bBSCnC2grcYEkX1HYvgZNzi3j4bB+YX4ZdUNaqeOilZpcq1uGFiSY+ugJ1FsdgXGnfpDYkPzaMePKJi5i4qmmW3fhZwhWQtxO6lluSjctQplW4mp0AxzGkfMbbCpic1IDZGYkWrRA8ZP3aSiQ4lpdUPZpb3I+/kPGqNkrjL2gmFoC2JgSSjSJANIPHxo3JMWLmMncpeQtsSDjk6+mIDSTTRPyZwqcvAkJqX2x9xW7QYJDWYOMGRXINa6bf4RRUsOQHktidT9xAlJbGHcMbR8HRBB6hoE00FDUOYtg1m/ThAb3kLOnK8g20rvjbCVtOlGj9Runukc3IyNjRuAJlbt2d3uNAgh13Ged6voXr9JzZzRecjr6DyY1C85V7H1z+8w7ed1uJilRMu+Y/H26F5wttDx3kT4vXtg6rweUJakYfeC/+EvWhR5vN4hu9+rWnqhxnAP6Y0J9FHKCnE1dhW+/Hg6/j5O3sXObfDax5PQx//24qEmzlpWWgalgTkRT2s4ONLAUDFRz8DhZd9gwtXr+Ph/k/FEO/JSZRvt/SayAYYP/gB/DiY6VJCKA6u+x0efz0N8ugFadhqEl8eNQIirDg8DNG87ED1a7kHy7v344MVh2NwpCq7G5BB0LA7xN3Jh08yVHIFIWr3f9miek8CYJy591MpilJ7ajNwv2cZMqiwm8q98SN7hep7eYhOYhPWjT1+oydO/KGYZ8n9YRCpC0t5YBMB8DDu20ElY9aSVmqbRgmva9hn6kARUnEEescQw/LpKo2oXubaG2YhhMPK2Lu89ceKZN0kC5gWWrk/TgsiJJajkkyj96wzK9h+F1aQ3YdrGs0EYDa5Hfj0e8liSSErIEY/7TPWJ7cxovSFVo4Ux2RLJDp7Njkx0396ZFhCSSnTYGNhA4m4GOo2ZBkQSlNn3T8jpZcHaLRIvfRBJknUJbp7dhR+/nIa/dpxAqUVLjBg/HoM7Noe5nlSiwYf6UFpwC/EHtuEQqd7LSIVpIDKBqRHb1wlOdnysz5inPnYY8R59iPaUpOPw0s/x+nu/40yhCQLbPoZJ7z6PYJKqqk1kLriyezmW7r8BudgevV6aiEHB9XQ2rVSREllJJxFzgIj41TQ6HUxGr49OcqMdLQry/WAaKaI1qHn0m1hMn+KMC5j/+SoqgX/T/l6puLp8ERGT2mUEfai0MiLQe/5AwfSlNI4IbzN/WH00EVKH27ioZfkoPkw29XnkL5LHZp0ISPzzaexd5ZdE4NaPsbjddGKQbQJhN+ELjUas7PIh5P44k+zTKTTEyPQ24FmY92jJwm55EsO06xAU/RFPKm7ykZn1nu4H7V8LHxjTDhOpi25dq/xznb+pslCyfx+UV2mu6/ostSVGljQo9F1E3JfY1BmWT7wCPEFmAvJ9yl30HUr+OqhhfsTe/WH9+gDm9WuV2NmS3/XDULE3GCHnveRM0OvVCVKNF5GjyNa/ZuHrn1bjdLoS/p1H4v3JY9C+uUM513snpsSRcr18W7su35mhVt+VNPgvH16L78hhbP3RaxA7huO5tz/C+EEhMNWTrsWGJvBtPwDjxtDEDRmGkYOiYEXOQIc2zMV3MxfgwJG1+HNJW0T4uSKAti/p1uFaNaKaTPLiNMSsnoEpn/2BY2ki+Ef1w2vvTcTA1q6sjC1PZA907YhXP3gd2bLZ2H0uGSf3/404JZ0hTplYAycinakhfamvgMkV8nay0pObkTfjZ6jIZkmiIYyHvweroTpOV9cuTW4iVOS5HrMKBT8tJBsv2fnMvGA66lXarkbqYaYADZbKifiOv1D4y3JyeqNFzCEYZi+Og3lH30oEWS1ntq88sYOOuRXtgrGnhY9MB7lFRNDJqW/5Jhj6vERbaBpiYRHBOHQwLN82Iu/+c5AdPqjx4lcc+BO5bl6we7U7LYZMDWhx5sQ67krqExpJBro3To44yvqOLKqOiHjK2d347ZuvMH/zcZSY+mHQS2/ivyOj4W5dXZ9FMLPzw7D/fgVz392Iiz2Mg4dP4vrxDfhtTnN4uo1FW2/CUduD+/yX7LrMuK6Yjren/IITucbwjeiPt6a+j4HkrV9T2WW5Z7GStoMmFRbDvsVQvDm6CywbYrBX9EICj/CBeONdK0TsP4CYfYdw7PRF7Fk6Az/4t8D0V7rC9vbeOHqK3g+tS9pUZ/Giolb9C1VJFm3hXIiCH5YRIaTxa+YNi7en0vYzR71sKtralYCCBQuIwaa5aUAOZV7NITI9rR1f5O1fdu4EXWdA6uUHqaMe461XSp0uyaxVdvkw8n4hIn44ieq0hLT7SFg+25vU2/rjiOZnIc1/DdUhbIzI1MSMH/kQgLYwQ14IJZk52aZuYKkb63VqSeXMBqSlfOU9FDWnnStnYqGIJ1NWMfl+zJpJmoAvSCAhRlmTiIjnJCJ/+S8oWbKP2kKvzr0LrN57FUYe5pXLvMs3PnqYj39libyu6vi7FFurnxqEkDMXwuf6cgf4vOH7SyoU5VzDjqU/49ufySOb9vL5tRtMXPh/0SeC9infpaVimjDaKXN/E0bJe9GPrMcP33yPtQcukaoqBEPHv4fXR3SusoecdLZwCeqDd77so9dNL0QPewmZVy7gSspGnE84jeskWfkSIb9Ls/Wer/6StQ2HVxER//QPHE1Vw69VL7z63mQ83Y04V90aoXuUjE3N2ozE9N9DsX/PXhw6dgo3i8xgJ03GhiV/I5ekYytT/Umle7Buf7VEfAvyZv0G5SWyLUmsyJb7Oqxf6EyOYVWXWY0kTtJBwS8LaWEh25RpM5gMHwfLQW0abNuZrgdqsjcX7V5KRJwWuiw5RHb+MH3uVVj0DiOGoTJgEkc3LaFk4mndClYfvwezts2gSD+N3F+/gWzLGVLHxZPzWRYRclddFXX+y9JR2VWShFS2xBS4waL/c0B/2iqVdZ7U7O9CvisFsj1bIH+qMyTk1yC2oYWDbdBZFFQiixZi3orDTVdkkQ8AqSs5GTqRurJyf7Q/1P5flbIUqbQPe+6M6Zi3gfYmkyNb72dew4SXH0eAi9kdBJPUyqnncY7iGDj7B6NZcHe8HNwNz+ffwM5F32Dqd3/h9JFDiDs3EOHk5FSf/dLyghTsW/Ydpkydh+OpUvi17YNJUz/D8I4e+mbLyh0lFerV/euwPi4ZRWIXDB37H3RwN6yc5z6/sQ9NWvIV3CqkHSo+XoiIHopW0f9v7zoAo6qy9pfeeyUhjTRK6F1AkF4EVERQERvqWrDub1vdddVV1117RcG1A4ogIgpSpfdepHcSakjvuf933jBhkswkM8kkJvCuPjLz5r5bzrn3nHNPezdgQtpWfPHKU3jt2xX4bdZiPHBrVzJy0ecaCg/nGjGvHZaMrVF4zj/Ltf0NhWERUMlpvOPgdd/fuLYTDOujrCo907P5PuwL4vDFQs1Z8ervDZ+1f48j96MXkEtNpNsNLyL4sd5cbyY/2/qRTLjg0HpkfPoOQyoPk4nTzNDjJvjdPYr+MxXCyFQ2smZ+yfFTte/NvXnX7dwTPjS9pSF37rcM+aLj2eJfkN+NMdxdarrnaLc/c4TCTCacm8TBNaobXCd0JwDz6L3/JS48P4m0YStyV+6De/OOhJ0wcfpmzfiUUTRLqeXgSb1pN/g+PpHaxXCbYFNQQD8dnsr5auN6Z+S1QWEZyuWF9CdPnoSHhwciI0kga1CKcphAYe4XeOej6diaVoLkbiPxyF8fwUjaXL3NJIIxdqEJvbJbOBM5kNtcGE+bupuhLe+9j1nL9/ME1wajJjyBR24bgOjAyiFkqrQQ5xiis3HDNhw9TXWVdoCi2pShWA5OXAQcRwlPexLXWqvCRb/z14/wtxc/xbrjCkkdB+HBZ/6OceVixyv0wM79o9pi+G0P45W3P8XnZEgP3chF6ewKZ8bF+3oabLEVnrL+K+1rEk6WOfkzlDAhBVzpkDX8AfjdMZASdGUhQZXk0Ya+BFmf8nRwhEzcO4b2tHvhe2MvOPnbh9CWDZ6hOHmbf0TWR9MY6kUmHpwMj3EPGQSGSpyFtrFYJq+JNIzZwZvangCeDhh64hTAELHIi7Z0eiyrQqPHbVlPNn0oSt2AjLdfQfrL7xEWaYZTETmzk38s3Nomsi2uk7w0El+uHc9guCTEUIXiSPPDLuQuZ3z+GWoHBI48ORdv5WmGxTGSITW0k9a4UPOVweQu3330Jj77aR1P4vEYcNP9ePT+m9CGjJi6gAolDxtn/AsPPvQ43pq6llofWfQOcPMJRULLJESGeiCXTl/p1GQUiY65hkUVpWPjnEl4+fWvsem0AxI7DsXjL76M8f3iDLHjFtotzNiLuTMX4vCZbIS2GIZxw1IqC7oWnq36tiFnxIwPn8djT7+C739nkhFNResI79BEtGWCGm/6pVxIPYMLjAipOHONLNUCTcaxqWKGkK35CdmTZxg8vn3iyQT/yrXdRlMPG+sZ/jKGPjIFbn17w4Hr2MGf9mYvChguxKqMhc6WWnEkwz9HM02tCgXS83uR+fn7DDU7rJ3EnbveCL97bjYxY5l0UMIQs72kGyzObRkzfjOT2fToBe/+g+A5tCdoQaAz2lk60FFgrQhMk2aq/KiykD3/c6S/+Dwyvl7C8DiaraTQBOTeqjM1rTxakVaU0HdIiiSCyf7tG+RNX2xg4mT8Pg8+BK/OsWZgqz1S7T+10kpX27r5CrU5MJa1KEZ+kUZqXkpw4eQOzGcY19rdp+DRtCWSkmPBDCf4ddZOquudNPuuq1co2nRh1qmAS0xD6Ibxqkn/JXlnsWkJE1ss3Y60Ah8607Rk+7nY9PscbKF04MgAfydnN4TGd0QXSmilWccwb8rLmPL7eZ5MOtEpqA0ifIpxdPtK/PQDHfMy3dGmbQtEBVQ81dg2uhKGSUxluMvy/enwYJa5pLZt4UVnnrkzdmhqcrF3e/qGI7klx9vEz4LZgQIG448z6IjmRBWXD0/ktaErkpQib9l8FG9L5Q4gbBh+5xhUwJCSX7hR6DQmMeX0sneJYjY1ErlSRiLkLpuL0v3n+bsb46dj6bzFJB9LfzbUJ2xBxys3xuK7xQXxnm0wMq2tCs8iezaZuNjfndhXFFXpDqnImjerrC8HD9rtWqXAtQkTePi1gNfYnsh6g4laji9E+qvZcG3fguM5xxPyZi4qRh8ERsE51GhXN+3Nhs+MRy1NZ+zu4SPInBKIkhE9KCwwPwKd7XJ/poqTa8whmN7ZvOdA7YZ7++7IS6Dn+vZzTGAxBelp2+HUhPU3L9PsnXDkiXdkr0oaBhtGRNNILg5v/A1TZ62lKtodiQmJSIh2xcENv+HIBpqptDXviqDoVuiYEkNBmqccek4f2bMBpye/iXDvC+gaH4DCc4excv587DiWA//wUESGBfDUXHMkFp7Ziq+mzMJmakFKvBLRvk9XeKdvwo/TN3B5kUFxfXn4Unho0QrxkUaBowjHNizAvA2HkVEcgtE3XYd2zORmr6IozGWdS6XGgclXXL3hnD8czUNdcP7YDsybu5WRIqWIbBOLMDoGVpy56AdrIdeUTaE06zByf/kNpSeyeY+OVAktCI9jyPrlBJcP1ynx5eDmBdek9vQ3pSNqUDz8x/8VBb0OoPjEaZRmUp1O35+iVUe4bwPh0m8QHT+j4HFVT1l+NS9yGt+9BIWL9rJdakX9msCZGqSC7cyotp3fZX8zQY9zBB03W0TTkYz5OcK9ubZzqc1bhIwZhCdzKpSmH0HeotWM3uBWDQtigiQT3xCbR0eY52ZQ4DmBAh4MM7wKKDDH0LfgNAo2LkIpD4l0S4czoy9EWig6uQ15vy2mqYJaDlfCLjGGTH47MufsZD2BLfelewA8OnapYCawPLD6zrMuI7ELI5f3r2ZnZxtUSTXayJTsCvORw7CDQq58B6pa1sylam0e1wdPtg4Mn3LignXxbIKRz36Al0a3NFl/VENSkJADsKjY5bKp0Pkjl1nQ8vKJyGJmu+LJZ8rhFTwFSXiZ9EuGRUYe0upu2gEfRAylucxzx/HHZtrJ1q7Cgp/D4OfO9JWnz3JTO6FZh6G4dVRfxAVTTWrTQMpXVsW5uHBBhCOBTSY2U8rc+RvD67SJOtK0RMcz/2a4/u5Hcd+t/dDEbKrPUuYdoYRKdZEbT+XedjiRl+aSUWraBsI8dSvyvt1x8TvhLjZdCf+K7gPn156jqp0esrQZGaTrIp7K1yH3yw2G+oImYf6OrsjrMAEhL91kVjVfHiqWvynxxs3k2KSIxL17MXL2LGHfXBiyJqQvFx8UXvcQQ7roUeznAe+BE0hwUpkdi0krqGbO37vSQNjEacsjEm69rqmsHjT0YPW/Lk07wL1/B+R+9TtKNjLhxYFlbJvDYggj8orp5BYH92HX0rHNcA52je0Ez2EDkH1yFlWAx1C0hM5bAiuBOb2GnDrfwhSb8Vb3b66i5rDJhDTZEjJa6oKzhzdi+scUEJnYp1TCFEnAnGiPD0wchX+/8zh6xPmi48i7MGT2bszcvADvvXQQs8LoQZ95GsfIKEo8ojFkyEB0bdlElAk1LpJe9wJPUJo2qzAdG+Z8jM2zDSGlQlBlTB7+8Rh08yN4/L6+CBPNRUEa1i1cjgMMz/KLH4Xr+6dQ8DDAssYDKXvQET6hCegzeBgWrvmYwv10vL5/FUKYoS3j9AkcT70Az8hOGD2uH2K8Lx0u5HFFfAnt0oJjZU8IDmtYVFEBQz7zy/bRpbXNdcp1bVjbHnDuwDjuv4+hAxdplncwhelgoDU75d7IALU7VF2jmCGyI26FV0eqrmuBK8NUmMGM4WKa0yiXp8o8gvwf/yeTN4xVowfOdBq+Gg5/exAeLegQy7VetJbq9TMbmMiGZkx6tGtt5JDWuYYyYmQg3JJDawgpPubgBy+mWC5YxciO3YdJn5ix7VcKBkyTrNI5VkU/odYDqAmIY11+Jd9RQvs5fhRTw7r6JxStkclIW6yg0Q1PFI9/DQG3ttWeqW5woqEWc3N9Frswcsm1Ljby4OBghIbWBAn0oo1ohYHXXY8DmfOwbe8xpB46QA/d8iUg0oNJTbhITIqjM0OvmvLEmhiH/PhkRIVeslOZVLP40dEjGB2YjW3U7lTMX7sTx1KPY/8JEliT4uAeDPe4Am1TulM9PPTOJ1Ho3xJLVm3Grn1HcC7dGSHN2qFHu54YfsMoDOmZBG+J965FkXCjGyfciEPfLGYfh3HkwN4KrbkhONoPOaLSs7hmnOATHoOUFNp+m3dBfHjtTuQOVKV7XNUfxQeo/tpBoiBMnXugfOG8LyYScfQMgUevoSjek0nPUaqVC8jUKyhuFBm5tpEM3L58UzZ8c3ANhidDdLLPzKcTmTBJgxratAnFk6ViTm5jV46+iQh46Glkhk9FwYrtPPGc5obnSSKKyWAYZudzrdjxa4dHB9cQ+Iy8gwzHHQXLmClO+qCCAr7BcGrTEu79rqfdvLXIP1pxcAsiIbqZtNAdefPocbvvOMPRyA6Cm8K5fX/aHseQ6ddu2zpSCxLbfgBuHb0TM5dvw6ETaThwujwiHXg6SQrLvagqd4B/4kA8+rdUeH4xB+u278a+nYdpTolEUqfBuKrfMNw4ahjre1U6lZrCv7rPLqFtcfNtI5HpsRBb/ziEg3srrHn6pwRF+SOX5g6K92XNuXj6IaRJS7QYc6OmKagN0yxr9OIHJ/dAhqeOxSMZJZjG5C+bd+3FTmZR8w+NRbfBQ9BvxFiMHdKG+7288ODs5o2o+CQkJ+QjoXkigmqxjpz8YhmjPQA5Gb9Qs8P1w+ROxjVsHK9yIkwkHam5Qmbk3CQRjoFbqHFqxvVDSfIS+Mw9Yd09pvR1a9EHLr22Mx3qISZVobCRzcu0cGErOiAaBFFqETuNRclEZsf8mc6eRxi2ls65uPnCMaEN3HoOhvfwa2g2qo3ZTcxmPeAzgZq/H35F8c791NJxD9FHyCE8Ec6t+NtNo2k7N/AJlwiaYfr354GHGq/TF0jTROtRvpD3UxYqz3fK1yj/7c94jWntKMLF8cuJXC5RfdXsdab0uvaPxjU3PcwXJAzGgcMncC6DiQvkNMxLSwjDU7d7UDN06dmsnCDp4OxNL/Lr8ezrrVHkG4vWkbYRE4k/btZpKB7+RxKG7D+E45Ts82kHk3610z2lyxIHH8TzxQ3NvClZc0HEtGMMblxHDLr+IA4fS0NWoRMCwyMRHROHqHB6cNvhRODgEope4/4PIR1G4NDRo0hj8g7RTDiKhCiSJFVZXoHRaNO5PYIpgZst1GJEtr8eL7+VhIKAFmgZwhVZm+LoCQ/G7zsFJ/AlKIeZCOYCwzi4wDmui4PihnWl+ror1WNUSxE3Hp2HwykkmfWPaDY5RZW8oT4HQtg6uBBebbtS7WZhDlaO18HJA1597qQarxvV1icYnkXpW04r2tikrxKeUnhibM8XlfgY4cA4UXq1+9/xGAr7HObLU+ixXkCiR8HQrVmMdmq3svsqqrGP0BT43TYRhb3YxxHCLZ3EJorOW9GxJCjhVIuazl3s51EUIu6Ae7s+hNsh1uc7B5rSpp6cxPHaJqiaHRhD9YITrsKEZ8PQi7Hgx9OYFpYxtuXXvKeWfrhD5MV8684+aDvoTjzfvCf27z+M48S9k28TxMbG8opCiB+9o2vJHJw8I9Fv/GOIYijlocNHcVpSZsqa56XRAPoweAREoW2njgi66LzowFNc73GPIbB7Jpq0aMsXJtVOWK0ML9rDQxIx+JaJaNV9KA4wvPR0VjF8Q5oiLi4OsTGMMXd34fjKFxeeiLvTCfS/LU7DP64NNWblGX352lV/c3ALYBjXGDqGdWKa4WNcD1zb3P+X1jb3EQUvbR9dzDtQvkUnRkyMBJ5Iopo4Fi6RtVFdm7QsAkJEBwQ8+hzjxw+hOI2ZJiX9q5EeaNIG8yhw/m7NAjThwcGNgu2198CtTX/ut5N8oUkeHLxokomI5p5oQl+58poNk96s/ujAterZfSRcYtoTXhzX8VM0kTMJExMYucbEkjZxD11EmJMfM8xdx/HwBTtFR0/QdMo1JxxGaIfUoZbK0TcKnt2Sy56xNBA5xHrRH0E81xvlidwuNgFKbt4BTdGmG6+uYlviMdOBkOQl8DQAhp8vIqAMmPJcYAy69I4pu2XrB2d3X0Qnd+DVXutHpH3tP60vUZFxGBTzy7pmn17+4WjeXi5be7O+vqtvBOEhl0FNp4U0lIOHgKdsVGYapkOSXzS69o0281vNbjm4+cAtvq12GVRo7F/GIMMQnPH/S3pEqmkJW/fmnQweoprqQCqa1JdhVDkHqWBNYV+0gXu0vYoXB6GpoqUf6Y9F65t/jd+1m4Z/HD2CaMOTy+SmXT+SOfuFc1xydTXAyMw4LnUpcGM0QALhzJOKJKa4tPgu1arNJycXD4TFpmiX7C0BjwzJsJ4M3+XGRehpXTm5eCEyoZ12Gfen6e+1GY/hWRHoI9GWiUXaduGavzgoo7nMQAOMY7zYG30vRBvWt1nte7fYAom6u08IEtvwat1VW+JV7zuOkdqD4JjW6BNjsVUbfuB68KJWMEWuLjatbWMnTn5MW9yzqfGr3f460InWpWkL7Srb/7IotPXNRcX/DZ8vdengzPSpzeiQx6uuigj2rlHJ2lW2uM11RlruFBBBTUEE0FHGy8uwEQy1xUyg0avqV7qPjw/kxSlyIhf1en0Wu5zIjRvMbgMXAqIthEstVvx+6Rd7fjL0Wx5l3ESmByZ7dmd1WzKGCqOqAB+rm7JnRaPUamxT2wDGLxX/cvwVx1zxe8VHavydfVWAV6W+a9x2bR8UONjShq31bWnbUFf2VnlUVPxeuc06348ckJGBG3uv8z6NHVX1V2BV1e91/ht7b6hrWxZROeBU/F7nwDHfQfnFbb6O3NXGX24CvGc98Teuz/pm4jJ060cptfWiQ0CHgA4BHQI6BHQIVIJARESEFkNe6Yd6uFFrRm5QyzFZCRPFiyRSu5en1M2M/4xMO9XNRPLTS+KAhlYkF0BDLKKyqu8XEVgDB7HfyvpqaEXWlvisNKQiJ5aGCCsZU+3fF1E7SHt6etaugTp6WvZcQ1tHsucaIrxkXFLE8bu+T+V22enitS52gXPnzuGzzz7DIToY1HURoiDvf62qpKamMoTrgma3eOeddzQikpxMp4U/sYgjxF5648oGOXHiBL7//vtajUacC729mUnBhiLPBAYGlnsiIyNDI2ZRdMI6fZqesX9iMaqoZAiypsQHQ8YrxPbPHpspWLL4rmkhKCKJN5RxnT8vLvHQokckt0N145Kw0VOnTplOy+6fhajJWpd1JwLGqlWrrO4jM5PZ7eqoHD9+XKMNQkfWrVun7cs66spis3v27NHgIo5S8+Yx3tZMMd0PZn622y3Bk9AnKbKOZP3IuHbs2AFZ6w2h7Ny5E02a8G1pFOxnzJjREIakOXqLs/fs2bO1vRQWFkZTuzgH1F9xYIdajzfffDOmTZuGbt26YfXq1VaPQGK4f/75Z4wePVojuMY3wFjdgF7xsoWASPLixWlLkWfaMvmNrUVCH+ujCNGvjxOKvLtAhOO6LiLoHjt2zKZuapIASpiErf3YNKjLuLIIiw1Rk3EZg9zmqRmFLRGMr7vuOnz44YeVDkvVNdq9e3esWbMGY8eOxdSpU6urXu53u5zIhVgPGTIEaWlpmlqhXA9WfDGq562oWq6KaAKqKkJwRNUvQBaVsRHYlp6xNA7p56K8U/bXUhvV3Zd25IQpEpycTkxVenKvPlQy0oe5SAPjHM3ByRJsqpqv9CEnfVvL4sWLbX1Er69DoAwC5tZv2Y8WPohwVpPnLDRn8bbsd9N+ZF/Jvpd7cso0V+Q3c/vVtK7QuurooWl9az4bD2VGlbE1z9RlHSN9EvolYzKFY132W1XbMhbBm/AXGZNoR/8MeNmFkYva80emV61pEWDICcSWIgtb1FJVlfT0dPz++++aNNu3b99qbayiVjJn4xd1joxRFpJIXLUpsjlEXSyXqK1MVdxiCqht+9aMTfqoqCqTuRmJhTmCIvMXgqMXHQINHQLm1q+5McuaNzIHUfubCtXm6tvjnpysTccne07olJjaLJkK5ZnqfFdkf8pByl7FeAiSdqVv0zHbqw9b2jHSHoGXaKpE8KpOSyFzMOLX2r5sFRCEZxjNEcY+BGZGIch4r67/1pqRy8Tbt69dMLVsIF9fJimwsYgqoroydOjQ6qpU+/u1115bbR29gg4BHQI6BHQI6BD4MyBQa6/1P2PQep86BHQI6BDQIaBDQIeAAQI6I9dXgg4BHQI6BHQI6BBoxBDQGXkjRp4+dB0COgR0COgQ0CGgM3J9DegQ0CGgQ0CHgA6BRgwBnZE3YuTpQ9choENAh4AOAR0COiPX14AOAR0COgR0COgQaMQQqHX4WUOau8TvSVpBKRWTrTSEcUospIxPwu1kfH9G4oCGAAfTMQjOjLH7Eq9aH7G8pv3X5LPEsUo8q4y1uvjemrR/uTzTmODUGNdhXa0Tib2W5DJCryR+XGLcG0Lylarm29Bpf1Vjt8dvlw0jlwQnkjtZECoMUhZifQflV4cQIfyyKWRcksxAcnRfyYxAcCY5uI04EyGnoeHMHE6NQpgwqoCAAMTGxpqrdkXfk3SskvRIYCU4NQrYDRUoQjOMY5UxyjsHapLboqHOz9pxCfOW3PuSuldgIriTe7YmVrG2P3vVE9oqQocI2EJjo6OjG+SLVew134rtXBaMXDKVCUOQF7uHhITUSy7sioC05btsDMnidvToUY0JCAG50oqcwuXlOpIjXXDWGLUTMgdhWAcOHEB8fPyVhkKL8z1y5IimZWnWrJnNufYtNlqPP4gAsm/fPsgLlmx9IVE9DtPuXYlAfebMGciLamJiYholIzQKIrIGRcC+Ug5KjZ6Ri6Qvr40T6VlOuI2hiPQoEqMIH5JWUaT/xsjIagprkfJFiAkPD9cYeWOduxD5pKQk7N+/v+ytRzWFyeXynDAC2ZPCxOVk1BiLpE6WsR88eBCtWrVqFOae2sJZTtyiIZN3I4hQ2lgPF0JbRQgR+iKahcjIyD89vWxtcWPN8/Xm7CbSXl2oZ6RduUTF2ZiKLDjjO3VFHdSQi+DNnipvMXuIGuzPesGAPWEtQohoFOojR749xy1t2Ruv0qa8M0H2Yn28IU76q6siL4ISZt6QTQJC9+xVZC3IaVZoUmNl4qawEE2f4M6edMu0/Yb2uc5P5CLliapq165daNeunfYuWXs6TshiFsZgUYWiaJ/Ly0GOJLenCj63yBFeVMGLGt7Lk28fc7ARJYrv7M08j4w8R/gHBcDDxQpZqDQfZ1PTkOvkj/BQf7hefEQYuMCiLk4usilr+6ID2QQi1Z48eVIj0F27drXLJhf/AMGZRQGGOCsqyNOYo+CtkHKOq4d3Gc6cHW1EGnGWk3EeWYXM6e/vBw9XvoGqKrSz/8L8HGTydJKVWwhHF3c+5w8fLw9U7FvwJ2tPYGSvYiQ+daWpkD0j7ykXjZCYBwSv9lqD0p68CMj82BVKigqQS2afnZON/AL6sxC23j6+8PHmizmcq8FLJQCXIj8zHRdyFbwD/OHlxjeYVapjckNbV7kaXjOz81Hq6EJa4At/Px+4uZTvWxib+EAYhW2TVmr8UeAu68U8bKxvVuzXQlO3bt2K/v3728WWL2OSNSDtmi/EXWG+RkdziLvsnEJtT3r7kpaK0ONcJeQrN0n4FuSm41xGEXyCguHj5lS5joU7ivs5Oz2Nz5bCLzQcAV6V3xoneLM3I7cHTbUwpVrfrjNGLhta1Bs//PCD9m5VsSM+++yzeOSRRzSCXOuRW9FASWE20g5uw+IFi7B201Zs27QZBy64o3mHrujZuz+GDO2Hds3C4G4DFApzzmLxl89h8qoATHzpH+ib4FU18YBC5uEFePbev2N3wCi888FT6BBaeeFZMR2rqxw+fFh7r62o7OW0KJe8WckWAiKEfsuWLXj33Xe1tkRVKu/Y7dSpk9XjqEnF0pJ8nDmyE6uWLMTS1ZuwbdsuHDtfiojk9ujRZwCGDu6LDskR8CIztraUFpzAb5PfwPRdQbjr8XtxTUo4LGFAlRbiwsk9WLbgJ/w4ewHW7k6De3ACegy6HjePuRYd40PhZivRsnagrCdEWuAuTKRJkyZlb8iz1ylJBLPNmzfjvffew9q1azU1quC1Y8eONoyyBlVJfLPOHsGWNUuwcPEabCET2nssHe5hSejcvTcGDx2CXp2SEOTDaA5rm1cZWPf9G/jwt3zc8MhEDO8aBw8Ly0LDa+perFgwFz/NXYA1mw4gzzUYKd37Y9SYMRjSsxWCyBBsZEfWjlR7w5nAXQTYmuJVDkVi+/38888xa9Ysjb5OnjwZt99+u9XjqFFFVYSM00ewcdlCLFm1Edu2bsLm3WcQGN8O3Xv2woAhw9BbcOdlPSEtLc7Frvkf4sXP96mzi2YAACTbSURBVGLEU6/jjh7hVsJeIe/sXnz18hOYtKwIY194H38dmWxxP9dovmYe+uOPP0iLtmkmUTG9BAUFaXzMFppqplm73bIe8lZ2KZKs2H3nzZuHL774Ahs2bCh7RalIkMLg5TRc16W04AJ2r5yFD97+ALM3nYVfUCD8vSMQ71tKxroWX21agsWrtuPJpx5A/7ZR8LASEiVFOTi4cy02bQ3D4VO5ABm5pVJckIOM80cxf/KH+H7xDjhHuGLLoUfQnoy8rgiGjOXVV1+FbHDxG+jQoQO6deumvaGudevWiI2NrfJULVKn4Ozbb7/FtGnTyt4vL+pSeW1snTJyai6ObvkVH73xDr5bvAfOQeEI5BzIz5B/chO+fXcNlq/ahoefuB9Du8TB20pmXpp/AYepEdq4yh/9b8tGcSlgVpFCZpOZuhMzPnwVH3y/GtmuIQgNCYbKO4RZH7+C/adL8J/nbkHLcL5z2BLSa3lfXrv7zDPPQISxuLg4DXedO3eG4E6umnpSC17Xr1+Pb775Bt99910ZXuX0LI5ddcrIeRK+cHwrvv/kTUyauhinEICwQD8E0UeipCAVS79/D8uXrcbtDz+B20d0RjiZuVX7ozQLx7bvwKZVGWhzYwaKShUZuZknNbzuwPcf/Bvvf0e8OgcgJCwCPqUF2Lv0K7ywg0z91ZdwW+9E0oG6weySJUvw3HPPaXgVoVj2pCleq6KJoqGR9TBnzhyNie/evbtM5b96NeFWl4ycTPz0gTWYNuk9TJq2BnkevggM8EVsYiyKKSAL7hb9tgJ3/t/TuJu4C7WSmasSOvwe2Ir1W/ai2dHzUFYy8tLibOxY9D9MnrYEBxCJbTuOImd4Evxt1dLZuE9lT/7000/aoUj2iuCvbdu2aNOmTYOww1vJvqybtagytm/fjv/973/a+8krqhvFU9uiOtW6LqyrVZqLQxtm4a3X3sXyE264ZsxjuG10f7ROiIa/eyFS923Cz99+gi9mT8c773gj+KVH0D3G26Rt2oQV4Eg1WKXCW4b7UoeVLJSijIOYT6l52ZoV+HnmahS6KziWFiGPEnldlx07dmj2TzndLV68WLuEEffs2RMDBgzQmLsswIrEQ05rsljltCZ4NC3yzl05pdddUUg/tAwfvPwvTN1YhM4jHsC4W4ajU/NoBHiU4syhrfhl+v/w+Yw5HF8QIl/5C7o2C4Tp4ViR4FHtYIYJOMCBG72ESC0pYR0LpbQoG3vXzcU3s9bBJWkEXnj8LxjQPgrFqcvx3ydfwIzFi7Bl3GAkhnjDBk2ghd7M3xYhWNSbIvCKOUquzz77TCMYI0eO1P726NFDO9WZb6HyXcHr7Nmz8f777/8JeAUKMw9i9qRX8daX6xDQZhieHHczBnRvifAAd+RT0F0zbxo++d8MfE7tT1jkKxjbM6GcYK0oCHD3cN9VnJsBr3Ao1faipd1YUpCObUt/wJcz18I9eRgefeAO9OuUAM+Sc1g36x089e/Z+PaH1RjcKRbRfnUTQSK0T5xyBa87d+7UrilTpmjM4LrrrkNKSoq2P8UB1LTIvluzZo0mmC9YsKBMADPWEQZfd4WHnpObMe39N/DxL3sR0nkkxo2/Cb07JCMixBO5Z6j5mz8NH386A1+88yZ8g17DPQPjYeriKAc7cEeaJaVEqANKUcI6lnBXfm4K5/ctxKSPZuBQMW35DnyX+8lzyKGrgH/dyF9l3QvOjKbGX375BXIJrq655hr06dNHE8patGhR7TvSyxq08we7MXJx9pk7d6624JYvX14mMZqOV+K868N5JPfUdsz44hssO+aJYfc9jUfHD0BMoHsZgU9o1w93NwlDgP/H+P14PjJzi7WF5IBiZKQdwrYNa7HxjzSUuvojOrEF2rZrjfgmvhdPYWLjoi2OK89oyzSdo/Fz0fm9+PWHH7GWvC+mx/WIS5uHNUfEwchYo+7+ilq2YklPT9ckejkZCNEYP348brjhBoSFhWlVN23ahC+//FK7pG7FIgRIiFFdFVV0GgunvInpazPR++4X8fdHRiIp2KMMZ77t+uKucJoIvCfjl/1AXgFjWy8OpijzODasXomN2w8g1zkIMc2SkNI2BfGRIQazCamICF+ltFEKM7dUSguycXzfXpwoDsa1I2/BiN4p8KWkUOIWj7gQP2AH7bFZdKCx3ISlpq2+b8l3QNR6cklkxvDhw/GXv/xF8zmprmHBq6hiv/76a029W7G+MAoRHuquFGP/8i/w4Ter4dv5TvzjxYm4pmUoXIxM2dcfI+4IQ5C/NybP3Eu7aSFxJMKWI1RxFvZtXo3VG7bhRKYzmkQ3Q4uUNmiR2BR+mj2MeHXiXmRbSpBiAS8l9Lc4k0bbb2gnjL33QYwZ3Ape2sndHx07tOYpcg5ST6Qik84YClZqA2wEmGhEzDmniZZSLsGrCGr33XefxtyleRGcRYUuDF/MLdJGxSKe9XVVVMFZrJszFd/O34vInuPwt/+bgB7JIdRmGZDnHZ2Cobc9hhBqV6bM/gO5GQZtl/gAFeacwb4dG7F23S6cL3RGUEQztKKPVEpiBDxF6yF7kkJ3qSK+uS+tKYUXdmP6u29h3l4ndBnYB+nL1iP7XDpyNRWbBZuKNQ1bUccc35J9M3XqVE37LKf0u+66C8OGDaux1syKYVisYhdGLiEnH3/8saaKlROEuSI2WlHLijdo3RaqZ7f+jiUbj6Fp1wm49bpeiKLkb6QbWt8OjvAJa4UbH/g7el8oRmCEryYZXjiyCd999im+nrkQ2w6eRomrD8Kj49Gm61Dc//j96Ns8kI87womMnEuQkqTl051baBuMe/hZjHAORDMSnhX/2XSRkVugNnYEyr333os333wTe/furdSqCFwi4cspTWKg77jjDu108Omnn2LZsmVlZhDTB8VpTgiNhOLUVck/sRLfztwE1+Tbcf+9I5BMJl6+OMArPAWj7n8KPbPoKR4WpJ3GSzIPYNYHr1JluhQ79x5BrksAIiKbod1VAzHmtvEYdlU83C8ycuHApbwsYcDBxQNNW3TDiOvi0btLIrzJxFVxDvavX4ZVf5yER9O+iA3zBX2y6qx0795dk/JF4Dp//nylfkTLJSd0wd3EiRMxePDgSnXkhggEP//8M4x4FYZdsYhzk4TnyEmirooqOoGF3/6MQyUJeOYvd6NPKzLxCp05uoeh+8i/IKpLFryDw+Apdg+VhW1zP8JLb0/D2h37kJZJnEc0RXLb7hg+ejzGjuiOCE8yAxcycseqoyqcPQLQvv/NeDIZaHNVosbEVQkF033r8f20eTiS6YRWKQkI9Kg7k5fgVU5ugldzgrLgVRi24PWBBx5AQkICJk2ahJkzZ2r5FiqATPvqTwfMXr16mfvJLvdy0nZh4aL1SPdpgwm3jEKXxOAyJm7swNk9EJ2G3YeoDmfh5M8EV0RdUfZJrJz9BT794nss23AA6QV0DA6LRGLLLrhhwiO4a3gbyO52dDRspGIrJGNVeArLvn4D78/cjbh+f8XEOwLxxcYNOFZIZ1hRclYkF8YB2umvCFiffPKJ5qNQsUnB58KFC7WDjhxWJ0yYUO9RVLVm5IsWLdJU6aL2qUr1KlKXqAyffPJJu8ZliiPXbbfdpjkHCYBV8Wns2bIDqRme6NW2FcJ8XFBYkF+ekV/EhJMHvchlAagCZJ89gUUzvsCU71aCEgBuHxwLL2dmOdq7AQtnT8JL+b4I+8+daKqYnlORwJOJF+bnIY+nX67dysUpEO17XaPdVyVZoJlOKwV5udpYRbAQCVvsXnJqsmcRIm5OejftQ5KxCEOQvo1JTcxJncZn5JQv6iRh9vYo4m0rDiMG7UEpTmynA1RqEZKu74PmgQ5l+KzYl5NnEAm43C1mNEImts55H699MBv5cX1w28Sx8EQeTtFZbsOyqfggqxjevg+hZySlflGFqGJtLYh2wdGMLVUpdyR2vx6PtGYURIA38rPO4uDGX/HxO59jwwU/DJwwEC3C3VFMWJSYSIYCNxGa3nrrrYrDtfm77BOR9KvU9nDdCOGQ/SaEQ9a/qTOcjGX69OnaJfZvWQ/mitEzWxj+0qVLzVWx+Z6YbmRPGrVCRWd30LEsFZ5NB6F76yCUEnaV9UXsxsET4QbEEkd5uLBnDl595UOsPB+FgWMfQJQvkHn6KDavX4Ep7+fAydsH4/r4oYQCNdk4oxwKNLW1W6m53cjTfHJXXjId8UbPxbl9izDpvQ8x9ae1KGzSDyP6psCLayo/3yCcC8zEq1/MTPYoYlIUvBpUzeZblD6Fjsp+FLWt+KpY9iLnTLimRSC/++67zTdo413Rzo0bN+4i7kpx8uB27D52BiFJg9E8muG9RYXINxsp64rgJhFab/k553Fg9Wx89ulUbM0IQt8x96BpoAsd1A5g1aL5eOeVXAQ2eQvXNXdEcYmiZlPR1m6goxaZkcrB7nmT8a/3fuU+H4YHJ45CsstKHuppKivOR25uHvIZsVCxCHzEwVoS3NS2yAGoOrOwqN9lvYiTt/QrTo31VSrP3oaexdHiiSeegDhfWCIWxuYEEPYiFsY25W/z5s1xyy23lKnsVVEWzp/JQkGRJ7y93LnYi0gYzK4+k2ZKcfbAeiygN21eUDvc++CjGNmdHrCOxXTS2YLwl5/GB3M/xY83DsK97al+E0ZO9V9hQSGvArNCgknj1MGTsRYLI5GFV6iNVfiALAxxQBKnwD+jCBGYP39+tV2LUCBRB3LZq8TGxmonFIPwUIpzHEtOgRMCQmnCEBhVhzIOpCRzB2b+7xccceqI55/5G0Z3joYbhbJ0OlZ9N+ktfLVkMeYv6o3mowM0oifMv4jEUtaqJZ8mBxdP+AV40gnrDDav+omaps+x6jB4YrwH44Z2RAANgIWFhnz+RlhIe2J2EMGovor0KerW//znP9p8hJgLMxev5rfffls7yQmjr4pxCF4lmY1c9iqSTETaNQqFBedP40xOEdzjQigYy7sQLGuxysagMrHmxy/x255iDH/qKTx7WxcEu4Oq2+NYPvNTvPvZYiz4dTG6tRikCWg0frBP2YtcN9XvRnbD0CcKcznZuaQTDCc9c5AC7R70oco/xNNAEmUOommsT5zK/AVuRnV7GTwsfJDkLWLOtFcRk9slWkrHzwvnkJ1fSDrK8DISrKIK695cv8UZh7Fy0WJsPu2BXrfehwdu6Y0IH2cUZKVhddzr+L835mHKtyvR45muNKGwUR6ISriW8znvipoaQ/tFOLJmKl579XPsKGqJR5+YiD7JfsjYLSp5eVyE8wLC7eJJyWRQIgxL1JQIRvVVpC8xY4nwIBoVCbWtj2JOfLW6X1ETyaKrjolb3aAdKjo4esA/1I8hQpk4fy4DBYWWFKmML8+9gJPHU5HFhXD2xEEcPZOH6Nad0TklDr7urnBx9URIs864bsRVcKMKd8WG/Shgcw607UipikiWn4qlMZSvdeV+c6CjDFWqKMSpo2nIqULVJuF/x06cJoHh6Sn1D6zYfY6mzyEY0jlW82J3cSPOYlqhx9XdEOGcgf30tD+bQ8mf6nXxaxBMVIe3otxTWP/r52SSH2H1cXf0u/kBPHT7UCTTT8LMQf5PQ5sIgkI4REA22hnlNG40nVQ3z/oYuJNvEG3QTsg5cxRnsyoTW+MYFKNBUo+dwLls+iAUp2HLsv3I8upMm6PBi93ZxQ2+wTHocFUvtI52xclDe7hfc7gX2QIRq+HV2Fi1fx3gH9MNdz72D7z6wkPoHpaFufQjWLonvU79H6odVoOq4ABPH4ZYebjRFMAcDHn5GozNDbGkKI95Mo7h1IU8ClunsP9gGhxCmqNb97aIDPRkPgtXeAdGo+eIYehIr7TtS9fheD735EVbu7ZOLZDIkpz9mDP5ayzZSbNZ7jH8/N4juGnk9YxweAurTp/DwQ1f4eGbR+P2B1/FT6sPIdfyEjM39Dq5J07GErUlwmB9lVoxclHDjB49ur7Gal0/TgyNaJGMUL8CbN6wBcfOZVLxVrkU56Vjzcw3MfHhZ/DtykNk+HJqLtYcMBwvLjDDU87wZCpOZ4cCCizGYyIlSZsKCY0sVKOt1qZnr4TKDghq0Qmdojyxf9k8bDlZaJ5olKQzbvgtPDbx7/iBnoM5eUwuUkR/ZmfXcnZrBye+Xc7DHa5OVNsVU/lqgUhUhizf+pR1EitmTsJr//0Su7IjMeqev+LBcUORFOFn8RRfuZ36uSM2bglJE58Io+QvIU2yLyVNZUMozj7N0aVzOPKPL8eS9SdoljI3KqpxN8/A8489hNe/WYX0HKpKeYqHA18yxEQtl4ojXNzcqXlwIrMv1hwXNQGtmu1YmHMKq+dMwYdTfsbBdANxdXL3Q1RSBwwefTfGj2yO4rNbsJE5A4q1jXqpxyv3kyMCI5O47oNwducWbNt/CnnmkEdtY+rOX/CvhyfipY+XIo17sqCoGKXEndjATRmMi4cXvOn/kE/NiWbqsgK4js7eCG0ayuRdrsg/dxDrV67EihUrsW7TbqRl5SL91AFsWrMa69ZvwoETF6hzM7vArOjJflXEtCQmZOOetF/LlluqlWpd8oWLGk9sAZI4pKrStGlTLY5SnD5qm3HMtB85iYj3o2koVYvugzCo/RK8L8kfll2NlPE9EVIu+w/jWjN2Y+PvS3DwbCT8AyMR6RKNEF8H7KT6+OSFQrSNMYQ2leQdwcoFy3G2tAnGd2mDQB8HZoESRw1miPNmRirGxFdDR2gfV2QqhlruXoascvJNHJAefvhhPEX1ob3LqlWrNLOHqN8sFXGoueqqqyCxy6KStVQkdlls2o8//riWtctSPVvuSypPyYhmxJu3xwDcfms7LHnnV3wxdRg6PDsCTdxNyQA91VO3Y/XKTdiXFsFMXr7UliSgdYg7Zq5dht3p4zEkzuDlnp9+Gge2b8GRXC9c3bwFYhj3vdmJbTGTl6cXM8QxG5VXOWHNMPLi3DPYuuQLvPHudzgXeBUe/OtfMXZgawR78TWOVUxO0u2KI6clR88qHjX7k+DijTfe0PwRLGm7xGl06NCheOmll7S85sbEFOIAdc8992g57F944QWLjlLSsTigGvFqrxTHYkKTrFpGvIoX0rXjR+PL397FrM+no3/XZ9CTAptpUUVp2LNmFbbtScOA6wLgG9gMzdsGo2TzWqzedh5DE+O1jHqlheex+9BO7D6Qw1Co5kiICcMRZ2ZkUy7w8PSitzD3luiAK5Ts3CPYs/ZnfL3OF94p3dCqX1xZ2KJyy0ShpgVwgp9/IHxpe3fhXhW4ixOgvXAqQ5JQMTGFrCQzsoRXSVsse1L2hoQMVlXi4uI0+puYmFhVNat/kxOkpNY14s47vhOGDemE5dtnMznSUvTokIAO0cboHUOzxXlncWTLMvy+OxXdrwlE04hARIf7I2/nIRw4ehalXePh50acMEfEzvlLsTItk34wXZHMKJBdkk1PhDXC3Jd01DSUtGzQPkkY+9zHjGQ5jUz6LzhyHzvQ1yV15xy89swUZLW6Hf/8501ICPBDSDgjkXzcy4QH2Ze//vqrRqvL2qvhB4GN+JL8+9//rtLmLmG9L774Ivr27WtXPlftsKnW0MrYsWNFlFEMdDfesvovbUnq+eefVyT4WhvSTsWLhEbRgUPRuUtRJWh129VVpC1CcbOVr1ZapI6umqJGd0tSIVFd1D3/nKKWbz2gzmUXquLCXHV813L1wdM3qqSIKNX39vfUrvQilXdqs3r7gSEqOiRW9b/1b2rqvBVq3Ypf1FuPXquaBnipqKufU5vPF6rc9MPq44ldVFzzfurj31MZ9VJ9KS0+r6bcn6KCIjqoj1acL3uGdlVFol19AzbW4IJTTPSheFqphAfBC4mEIhNQJCiKDFXDCYmWEhxVxJt8l3ZI9BVPeooOQDaOxnx1+lUoChnlfsw+uVQ93C9O+YclqhsffU8tWL9Hnb6Qowrys9XJfavUpL+NUS2iIlSfCe+o7SeyaB47o2Y83Vf5OXuoNiOeUN/OW63Wr5qvPnx+vGoXHaJS+t6lvlt/ShVm7FDv3TNIxTS7Tn0w/w+Vy+NA5VKszuz/TT0xLEnFpgxU/525VZ3PzlV0jFO036miEsYoVH5Iu0OBTDHu3sKvtt1m0h01atQoRXu3WVwIPuiUpJiNTTHTF101zI+KjEKRESi+watavDKhiN3wKnuxIl4Lc46rr54arEL8w1TnEY+oL39dpw6npau8gnx1IW2fmv/Zc+qalGgV03WCmrX5uCooLVGHfn1OJfq7qeDE4epfX8xTazesVD988rwa1ilONUnuq/7+1VqVUXBUfffMTSo57mr1z2kb1YUC87Aozk1TCz56SLVu0lR1v+Ep9f2y7epY6kl1YMcKNfkft6lWUcEqquv9asG+c5S5DYW2asVMbLYhr4razAymGO5ZJV6FPjL6RwlNo9+CokCmKLBZXAdkuopRB4oOq1X0bP1PVAkr2ZeXSinp4kb133v6qaiQpqrP2GfVtIUb1LHTWdwPxSrr1H41/8t/qkEpTVV8x9Hq6/VnmOflnPr98ydVj4RwldT9RvXqlDlq9doVatbHT6mrec8tqJt6Zxn3ZP4F9dvbt6iIpknqwS+3qmo5Ate5rHXtKslTB1d+qAbHxqirbvpI7c01/zTNvkr2pj0Kc6NoNNASTRU8yT6S9V9T/ia8V/a38GJbi9gLtVIbRi4NCEOgY4jiKd3iwpNB0ilHq2votfb/mmXk0mxpntr/+yR1U+dY5eNSmaExJEW1HfyY+mVX+kUCXaiOrPlK3dGvhfKrUD8k5SY1bcs5rV7u+QPq3fvaqKgW/dSny09bJO6mMxOGM2lCigqO6Kwmr7lQ9kxdMXJZdNR6mMUDPcUVw5YqEW56XCqGslh8TnBHNa4SIcEexRwjJ2dWp3fNUQ8OSlYMJjAzfj+V0v9h9ePGYyr/Is3OT1uqJvaOqVDXXTVtPki9/sNWlcXYlqL0reqtuweohKRR6pOFe6pg5AvUY0ObVWjLMA5HT18VHp2g2nUbpp6avEJlFlwiHvZk5EKUeUo2OwbBQcuWLdXGjRutRgGTAykmAlJC9OV5cxczVClGJFjdZlUVzTFybkaVc26XmvT4MBXhY15YDE3qr177fqNKz7/ISotOqRlPDlD+FYRR/4jm6vYXZ6hDF4qUKj6ivn5shEqM6qVenr5JZRSaZ+SsqM4dWqleuetqFepZuf+IttepjxfsVblFRjaulL0ZueCMpzSz8BecMLSzEl7psa6ocdEOQObwZrz39NNPV4USq3+rzMjl0VKVfWKN+vc9fVRYALNaVVxDjq4qNKE3BamtKuci+HJ5KHrvkeEqNtCjXH0H32T1lw94eGA9mjbVL/+5STWNaqMe/WZH9YzcdBZk5AeWf6AGxsaqHmM/UQfyL+1F02r2ZOQ8iZebiykcqJFWzKapGC5q2r3Nn2vDyGulWudkyoqo0+68805cf/31WnYw8djjptZUSBKKIh6EUsQzsl7ejOTgjvir78GUn3ri9wXz8duiZVi9djOOM9lH5+490HfQtRg++GrEBRkTQLgguusYvPp+NLpO+wrT525CgV8srr72Ztw+dgjDjgzx787u/mjb83oMhjNaxTAmxori4OiNdv2uxYB8D7SJ8axSTWtFc9VWEZW52A5Ni9hTRQUnUQYU2iq9ZIYMQlPlStIRMZf8+OOPmgOV4M6oBpR0nmIiqbNCNVtI86F4fWoKbqBZZN7CpVi1bgdO5bgjoWN39B14LUYM7sHkPLRXX5yeW9jV+M/3P6HDp59g+s9Lcco5HlczL/otY4ajfXyQlnhEeYahLbOhDQzxR3LTAPPpWeGEwKiuuO+ZfyLfdRKWbGcImJML3Dypwg8N1DKNFeZn4gy960+n59BPum6KhOSJety0iNpc1J2CN0m/a4saXGL/JUGTOKUKXkVdK+YoU7xKnxJPXneFjlOBzXHny1+ix8hFmPvrQixbuY4mkhwExnZAr74DMGLEEHRMDL/0EiLnUFz/8rcIbj0Zn01niOYxJ7TpOQg3jr2J6vl4+Gix5gFo2bs3+hXmoX1iSBU58Inb2G54+PXP0bn/j5gxcy7W/HEGvtFtcM2g4XRm7Y+U6EAL68I+UKkKr+Ip/sorr1TCu+w3SesqcckSTige9GJ2kf0o+COn0AZXp+l1Sa28IrrirzQ39R+ziFEuC7FiFUNF9+QhplNX9OozEMNHDEXX5peS/HiEtsOEv7+J+A7f4etv5+APeb8Fc3GMGz8Wfds1hRutXKXObmjW4RoMvyYEPVuEl6nDrYK2gwv8o9ph6OihyGndFsGyFuq4CE01LUJfxQbevn17LaXywIED7fbiIdN+rP5sFBtqeyI3tmP8K+o12l4V4+kU7YeKDEC7RPKvqerB2LbpX4snctNKxs9U2TFrlPFblX8tqSyrfMjGH+vqRC7DoK1NkyDlZM5kLmrMmDFKTt3WFoaaKSYTURTMNC2LqPAYr6xkzPYoZk/k5hq+qE4z91Ple1S9Vb5ZoztWLhOtbXueyKVBCluaOlxMHWTqSk7MM2bMUKIur20RlS0TWyimBS3D6x133GE3vJo/kZsb9UU1qbmfzNyzBR9mHrf5lr1P5DIAvjCqHF75NkjFhC9W00M5odPmq7UjpjDZk0JX7WXWMX8iNwe6UlXCFIlW7TXZv+aaqId79jyRM5SzTFsppkk6k2qazUOHDtltJg3iRF5RchAHqauvvlq7RKo0xiAnJSXZNSFMxX6r/M5YFWtlt4on2irbbYA/iveyJAsR72XabjRPZluGKS92kEvSDkq8uWSekuxukqiiXouEjVndoS11q260gkKj6sp2/lXgLt7oormSBCvyxkB7wV3ivOUSvEqcueBVTuP2at96UBBX1iPWprrWj6F+awpeRSMp2jEjXo0pkq0ZiZzQJZOfXOJUKC8xEqc40abVb5H0qlb2aNP+tbLNP6Ga4EwcWiW0THKXiJZEnE0bSrGbar2qCclikwVcV0WYrqjuRQXZmIqMm+JcnYxdUuaKZ7iofmpTBKYSlWDPLEWCK5l7YxeWjHCVeG57rj0J6ZQXo8hraIV410URj15741XGKe0KfmVdN3b8Ck7FDCFzske5+eab0ZumAIn2scU8Yq5v8W63p0pd8CWXveZqbsz1ec+IN3utQTFtSQpdKXWZ0rimMKoXRl7TwVnznISySUYreVevhNM0lmJK6IwhdPYcu2g+GmoRxienTYFBYy/CtOR0ZM93CEgcqlyNsYivDE0Nmk2/MTMFwausUQk7stc8GjJeZS+a7kt7McA/aw0LPxAbtr0EbGmnITJwI3wb1xHWOGqTv8LIBWHyggkhILIBG3qRMUp8t5yYZez14vzXgIAiOJNL1FSy4RorQxcBTOZAP41KjkoNCNz1OhQRpkWwkRdJ1GdmK3tOUuiIpGeVA4KoVK+EIoxKaJEwc8nvbnRwbWxzNwrWMgcRru0lhDV0ODT6E7kgSrx8xd4nLyWQE4Fcos4XZtGQimwOYd5yyYs7ZKHJ2Bu79GsrjGW+cjoRYik4E7WV4EvUhY1h4wmhF69hYeDCzIV5yRz0Ag2HsqZFUBWGLrCRfSi4bchF8Cj7UnArwqUI12K/tteJriHP3Tg22YOi8jceMmRNCy0Vgaah0ygRGgV3gkPZm4I/WYeNgZ4Y4V+bv42ekcvkZQGKs45sQCmy+RriBpTNIOOSjSFMXIhbQxM2NADWwz9GnAkzlNIQ8WUJDEY8yhzkFCOOnQ2d0Fmai73vCxxESBO4aG+Z43pvLMRU1qCMVYQPuWSfXklF5i4+GaKFkJe3CDwa07qW8Qo9lbUntPVK0abIGr0sGLlMRDZdQ994ssiEQOjFAAHZaMHBwY0OHMLA5dKLeQgI8RfhRq7GUoSJCfFv6JqDuoanMMPGhDcjPIS2ynWlasYavY3ciEj9rw4BHQI6BHQI6BC4EiGgM/IrEev6nHUI6BDQIaBD4LKBgM7ILxtU6hPRIaBDQIeADoErEQI6I78Ssa7PWYeADgEdAjoELhsI6Iz8skGlPhEdAjoEdAjoELgSIaAz8isR6/qcdQjoENAhoEPgsoFAWfiZJOaQcvDgQWzZsuWymaA+ER0COgR0COgQ0CHQ0CEgvFeKkRfbMl4HpsfUEl43psB/Wyao19UhoENAh4AOAR0CjQkCtqat1lXrjQm7+lh1COgQ0CGgQ0CHQAUIlKnW58+fj127dmmZcRryW14qjF//qkNAh4AOAR0COgQaPQR2796tpRmvyfvly1TrjR4K+gR0COgQ0CGgQ0CHwBUIAV21fgUiXZ+yDgEdAjoEdAhcPhDQGfnlg0t9JjoEdAjoENAhcAVCQGfkVyDS9SnrENAhoENAh8DlAwGdkV8+uNRnokNAh4AOAR0CVyAEdEZ+BSJdn7IOAR0COgR0CFw+ENAZ+eWDS30mOgR0COgQ0CFwBUJAZ+RXINL1KesQ0CGgQ0CHwOUDAZ2RXz641GeiQ0CHgA4BHQJXIAR0Rn4FIl2fsg4BHQI6BHQIXD4Q0Bn55YNLfSY6BHQI6BDQIXAFQkBn5Fcg0vUp6xDQIaBDQIfA5QMBnZFfPrjUZ6JDQIeADgEdAlcgBP4fmmiffearhrYAAAAASUVORK5CYII="
- }
- },
- "cell_type": "markdown",
- "id": "41dd9764",
- "metadata": {},
- "source": [
- "Two-dimensional (or greater) arrays can be stored in two different ways:\n",
- "- __row major order__, i.e the linear array of memory is formed by stacking the rows one after another\n",
- "- __column major order__, i.e. column major puts the column vectors one after another. \n",
- " \n",
- "Julia implement column major ordering, just like Fortran, Matlab, R. On the other hand, arrays in C/C++ and Python's numpy are stored as row major-ordered. \n",
- "The following code squares and sums the elements of a two-dimensional floating point array, writing the result at each step back to the same position. The following code exercises both the read and write operations for the array:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "654d6615",
- "metadata": {},
- "outputs": [],
- "source": [
- "function col_iter(x)\n",
- " s=zero(eltype(x))\n",
- " for i in 1:size(x, 2)\n",
- " for j in 1:size(x, 1)\n",
- " s = s + x[j, i] ^ 2\n",
- " x[j, i] = s\n",
- " end\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "511ce4f8",
- "metadata": {},
- "outputs": [],
- "source": [
- "function row_iter(x)\n",
- " s=zero(eltype(x))\n",
- " for i in 1:size(x, 1)\n",
- " for j in 1:size(x, 2)\n",
- " s = s + x[i, j] ^ 2\n",
- " x[i, j] = s\n",
- " end\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "66ea350d",
- "metadata": {},
- "outputs": [],
- "source": [
- "a = rand(1000, 1000)\n",
- "@btime col_iter(a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "bda3ff9f",
- "metadata": {},
- "outputs": [],
- "source": [
- "@btime row_iter(a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "b51f3b04",
- "metadata": {},
- "outputs": [],
- "source": [
- "#Another way of writing row_iter function\n",
- "function row_iter(x)\n",
- " s=zero(eltype(x))\n",
- " for j in 1:size(x, 2)\n",
- " for i in 1:size(x, 1)\n",
- " s = s + x[j, i] ^ 2\n",
- " x[j, i] = s\n",
- " end\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "e3891759",
- "metadata": {},
- "source": [
- "### Lower Level View: the Stack and the Heap\n",
- "\n",
- "**Stack** \n",
- "- The stack requires a static allocation. It is ordered and accesses are very quick.\n",
- "- Because this is static, it requires that the size of the variables is known at compile time (to determine all of the variable locations).\n",
- " \n",
- "**Heap** \n",
- "- The heap is essentially a stack of pointers to objects in memory. When heap variables are needed, their values are pulled up the cache chain and accessed.\n",
- "- Heap allocations are costly because they involve this pointer dereferencing."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "f5fece0a",
- "metadata": {},
- "outputs": [],
- "source": [
- "a = Int64[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]\n",
- "b = Number[1,2,3,4,5,6,7,8,9,10] #Number is a supertype of Int64"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "d0ac9708",
- "metadata": {},
- "outputs": [],
- "source": [
- "function arr_sumsqr(x::Array{T}) where T <: Number # with <: T inherits Number \n",
- " r = zero(T)\n",
- " for i = 1:length(x)\n",
- " r = r + x[i] ^ 2\n",
- " end\n",
- " return r\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "2af26fc4",
- "metadata": {},
- "outputs": [],
- "source": [
- "@btime arr_sumsqr($a)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "6a5cbd89",
- "metadata": {},
- "outputs": [],
- "source": [
- "@btime arr_sumsqr($b)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "37672634",
- "metadata": {},
- "source": [
- "When the array is defined to contain a specific concrete type, the Julia runtime can store the values inline within the allocation of the array, since it knows the exact size of each element. When the array contains an abstract type, the actual value can be of any size. Thus, when the Julia runtime creates the array, it only stores the pointers to the actual values within the array. The values are stored elsewhere on the heap. This not only causes extra memory load when reading the values, but the indirection can mess up pipelining and cache affinity when executing this code on the CPU."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "id": "350cf13b",
- "metadata": {},
- "outputs": [
- {
- "ename": "NameError",
- "evalue": "name 'rand' is not defined",
- "output_type": "error",
- "traceback": [
- "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
- "\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
- "Cell \u001b[0;32mIn[2], line 1\u001b[0m\n\u001b[0;32m----> 1\u001b[0m A \u001b[38;5;241m=\u001b[39m \u001b[43mrand\u001b[49m(\u001b[38;5;241m100\u001b[39m,\u001b[38;5;241m100\u001b[39m)\n\u001b[1;32m 2\u001b[0m B \u001b[38;5;241m=\u001b[39m rand(\u001b[38;5;241m100\u001b[39m,\u001b[38;5;241m100\u001b[39m)\n\u001b[1;32m 3\u001b[0m C \u001b[38;5;241m=\u001b[39m rand(\u001b[38;5;241m100\u001b[39m,\u001b[38;5;241m100\u001b[39m)\n",
- "\u001b[0;31mNameError\u001b[0m: name 'rand' is not defined"
- ]
- }
- ],
- "source": [
- "A = rand(100,100)\n",
- "B = rand(100,100)\n",
- "C = rand(100,100)\n",
- "\n",
- "function inner_alloc!(C,A,B)\n",
- " for j in 1:100, i in 1:100\n",
- " val = [A[i,j] + B[i,j]]\n",
- " C[i,j] = val[1]\n",
- " end\n",
- " return C\n",
- "end\n",
- "@btime inner_alloc!(C,A,B)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "cf21c41c",
- "metadata": {},
- "source": [
- "The array is allocated for each step of the loop. This allocation and the subsequent garbage collection take a significant amount of time."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "3284a9ae",
- "metadata": {},
- "outputs": [],
- "source": [
- "function inner_noalloc!(C,A,B)\n",
- " for j in 1:100, i in 1:100\n",
- " val = A[i,j] + B[i,j]\n",
- " C[i,j] = val\n",
- " end\n",
- "end\n",
- "@btime inner_noalloc!(C,A,B)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "29b01eb3",
- "metadata": {},
- "source": [
- "Consider `StaticArrays.jl` for small fixed-size vector/matrix operations. \n",
- "- StaticArrays.jl library uses statically-sized arrays and thus arrays which are stack-allocated. \n",
- "- It can be used for many small (< 100 element) arrays of fixed sizes."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "6058653d",
- "metadata": {},
- "outputs": [],
- "source": [
- "import Pkg; Pkg.add(\"StaticArrays\")"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "ec194cd0",
- "metadata": {},
- "outputs": [],
- "source": [
- "using StaticArrays\n",
- "function static_inner_alloc!(C,A,B)\n",
- " for j in 1:100, i in 1:100\n",
- " val = @SVector [A[i,j] + B[i,j]]\n",
- " C[i,j] = val[1]\n",
- " end\n",
- "end\n",
- "@btime static_inner_alloc!(C,A,B)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "c52bd387",
- "metadata": {},
- "source": [
- "## Bounds checks \n",
- "Julia performs bounds checks on arrays by default at runtime. This means that the Julia compiler and runtime verify that the arrays are not indexed outside their limits and that all the indexes lie between the actual start and end of an array.\n",
- "\n",
- "The `@inbounds` macro eliminates array bounds checking within expressions and is applied in front of a function or loop definition."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "7d10ae75",
- "metadata": {},
- "outputs": [],
- "source": [
- "len = (100, 100);\n",
- "a, b = fill(1.0f0, len), fill(2.0f0, len);"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b5dc2255",
- "metadata": {},
- "source": [
- "Using `fill` in this way is not only convenient but also safer, since the memory that is returned to the program is filled with known good values. However, the operation to fill the memory is also expensive. For a performance-critical method to create arrays, the constructor can be called with a special `undef` keyword. In this case, memory is allocated, but not filled."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "8cc42a32",
- "metadata": {},
- "outputs": [],
- "source": [
- "function prefix_bounds(a,b)\n",
- " c = similar(a)\n",
- " for j in 1:100, i in 1:100\n",
- " c[i,j] = a[i,j] + b[i,j]\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "3761b33b",
- "metadata": {},
- "outputs": [],
- "source": [
- "@btime prefix_bounds($a, $b)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "ce83d5ab",
- "metadata": {},
- "outputs": [],
- "source": [
- "@code_llvm prefix_bounds(a,b)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b059ee31",
- "metadata": {},
- "source": [
- "Notice that this getelementptr inbounds stuff is bounds checking\n",
- "- bounds checking is enabled by default in order to not allow the user to index outside of an array.\n",
- "- Indexing outside of an array is dangerous:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "603e50fd",
- "metadata": {},
- "outputs": [],
- "source": [
- "a[101,1]"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "ddd4ffe3",
- "metadata": {},
- "outputs": [],
- "source": [
- "function prefix_bounds(a,b)\n",
- " c = similar(a)\n",
- " @inbounds for j in 1:100, i in 1:100\n",
- " c[i,j] = a[i,j] + b[i,j]\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "deee358b",
- "metadata": {},
- "outputs": [],
- "source": [
- "@btime prefix_bounds($a, $b)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "b67a1011",
- "metadata": {},
- "source": [
- "When the Julia environment is started with `-check-bounds=yes`, all @inbounds annotations in the code are ignored, and bounds checks are mandatorily performed. Alternatively, when the Julia runtime is started with `-check-bounds=no`, no bound checking is done at all. This is equivalent to annotating all array access with the `@inbounds` macro. This option should only be used sparingly in the case of extremely performancesensitive code, in which the system is very well tested and with minimal user inputs."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "fc6b62f9",
- "metadata": {},
- "source": [
- "## Broadcasting\n",
- "\n",
- "Performs an operation on each element of an array, rather than on the array as a whole. In many high level languages this is simply called vectorization. \n",
- "*In Julia, we will call it array vectorization to distinguish it from the SIMD vectorization which is common in lower level languages like C, Fortran, and Julia.*"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "35be5ea7",
- "metadata": {},
- "outputs": [],
- "source": [
- "a=collect(1:4)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "dc548e01",
- "metadata": {},
- "outputs": [],
- "source": [
- "sqrt.(a)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "39c5589d",
- "metadata": {},
- "source": [
- "More generally, it allows operations between arrays of different shapes, such as adding a vector to every column in a matrix:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "db39c829",
- "metadata": {},
- "outputs": [],
- "source": [
- "b=reshape(1:8, 4, 2)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "eaab2429",
- "metadata": {},
- "outputs": [],
- "source": [
- "b .+ a"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "d2c913e6",
- "metadata": {},
- "source": [
- "Unlike many other scientific computing languages, writing vectorized code in Julia is not a performance optimization. Writing loops in Julia, unlike say NumPy or Matlab, is pretty fast. \n",
- "Even in vectorized languages, there is a downside to operating on vectors—combined operations do not compose efficiently. For example, for a vector `a`, the `b=sin.(cos.(a))` operation will usually compile to something like `temp=cos.(a)`, `Y=sin.(temp)`. \n",
- "This code has two problems: a temporary temp array is allocated, which is a problem for large input arrays, and gets worse as the length of the function chain increases; secondly, there are two loops through the elements of `a`. \n",
- "In Julia, however, code like this will compile down to a single loop, with no temporary array allocated. The compiled code will look conceptually similar to the following code (__loop fusion__):"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "2f126edc",
- "metadata": {},
- "outputs": [],
- "source": [
- "function broadcasting_ex(a)\n",
- " b = similar(a)\n",
- " for i in 1:length(a)\n",
- " b[i] = sin(cos(a[i]))\n",
- " end\n",
- " return b\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "037dfd09",
- "metadata": {},
- "outputs": [],
- "source": [
- "a=ones(10);\n",
- "@btime broadcasting_ex(a)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "e6e91e7f",
- "metadata": {},
- "source": [
- "Broadcasting can also help with preallocated output using the dotted assignment operator, `.=`. This allows the use of preallocated output with loop fusion, avoiding any extra copying."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "ab8f56ba",
- "metadata": {},
- "outputs": [],
- "source": [
- "a = collect(1:10);\n",
- "b = fill(0.0, 10);\n",
- "@btime b = sin.(cos.(a))"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "76d75064",
- "metadata": {},
- "outputs": [],
- "source": [
- "# using the .= operator results in reduced allocations\n",
- "@btime b .= sin.(cos.(a))"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "f8986c4b",
- "metadata": {},
- "source": [
- "## SIMD parallelization (AVX2, AVX512)\n",
- "__SIMD__, stands for __Single Instruction, Multiple data__ and is a CPU method of parallel computation, whereby a single operation is performed on many data elements simultaneously. Modern CPU architectures contain instructions sets that can perform these operations on many variables at once. For example Intel has such implmentation as __AVX2__ (256 bits of data in one instruction), __AVX512__ (512 bits of data in one instruction)."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "fab4c47f",
- "metadata": {},
- "outputs": [],
- "source": [
- "using Test"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "abd8a002",
- "metadata": {},
- "outputs": [],
- "source": [
- "len = Int64(1e7);\n",
- "a, b = fill(1.0f0, len), fill(2.0f0, len);"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "eba8facf",
- "metadata": {},
- "outputs": [],
- "source": [
- "function serial_sum_vectors(a::Array, b::Array)\n",
- " c = similar(a)\n",
- " @inbounds for i in eachindex(a, b)\n",
- " c[i] = a[i] + b[i]\n",
- " end\n",
- " return c\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "7289b273",
- "metadata": {},
- "outputs": [],
- "source": [
- "res0 = serial_sum_vectors(a, b);"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "0055b1d1",
- "metadata": {},
- "outputs": [],
- "source": [
- "@test all(res0 .== 3.0f0)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "c591fc81",
- "metadata": {},
- "outputs": [],
- "source": [
- "#The returned time is the minimum elapsed time measured during the benchmark.\n",
- "serial_t = @belapsed serial_sum_vectors(a, b)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "6b4b9d8d",
- "metadata": {},
- "source": [
- "The function essentially performs $10^7$ sequential additions. A typical SIMD-enabled processor, however, can add up to eight numbers in one CPU cycle. Adding each of the elements sequentially can, therefore, be a waste of CPU capabilities. On the other hand, rewriting code to operate on parts of the array in parallel can get complex quickly. Doing this for a wide range of algorithms can be an impossible task. \n",
- "Julia, as you would expect, makes this significantly easier using the `@simd` macro. Placing this macro against a loop gives the compiler the freedom to use SIMD instructions for the operations within this loop if possible: "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "14d275f8",
- "metadata": {},
- "outputs": [],
- "source": [
- "function simd_sum_vectors(a::Array, b::Array)\n",
- " c = similar(a)\n",
- " @inbounds @simd for i in eachindex(a, b)\n",
- " c[i] = a[i] + b[i]\n",
- " end\n",
- " return c\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "aef641b8",
- "metadata": {},
- "outputs": [],
- "source": [
- "res1 = simd_sum_vectors(a, b);"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "5ff6d6d8",
- "metadata": {},
- "outputs": [],
- "source": [
- "@test all(res1 .== 3.0f0)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "5c307d84",
- "metadata": {},
- "outputs": [],
- "source": [
- "simd_t = @belapsed simd_sum_vectors(a, b)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "cb457ae2",
- "metadata": {},
- "outputs": [],
- "source": [
- "#Let's see what is the obtained gain\n",
- "times = [serial_t, simd_t]\n",
- "speedup = maximum(times) ./ times"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "349e27f8",
- "metadata": {},
- "outputs": [],
- "source": [
- "#Let's check if our code is using SIMD: the keywords to look for in the output are sections prefixed with vector and vectorized operations that look similar to <n * float>\n",
- "@code_llvm serial_sum_vectors(a, b)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "23c3c08b",
- "metadata": {},
- "outputs": [],
- "source": [
- "@code_llvm simd_sum_vectors(a, b)"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "e543524c",
- "metadata": {},
- "source": [
- "### Limitations of `@simd` :\n",
- "\n",
- "Adding `@simd` does not make every loop faster. In particular, note that using SIMD implies that the order of operations within and across the loop might change. The compiler needs to be certain that the reordering will be safe before it attempts to parallelize a loop. So we need to be sure that:\n",
- "- Each iteration of the loop is independent of the others.\n",
- "- Arrays being operated upon within the loop do not overlap in memory.\n",
- "- The loop body is straight-line code without branches or function calls.\n",
- "- The number of iterations of the loop is obvious.\n",
- "- Bounds checking is disabled for SIMD loops."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "d9d5bee7",
- "metadata": {},
- "source": [
- "### SIMD.jl\n",
- "The `@simd` macro we saw previously is only a hint to the compiler, it does not guarantee that SIMD operations are used on the CPU. As a programmer, you want to be absolutely certain that some operations are implemented as SIMD instructions, the `SIMD.jl` package provides low-level types and functions that allow you to specify this."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "45f7bd3c",
- "metadata": {},
- "outputs": [],
- "source": [
- "import Pkg; Pkg.add(\"SIMD\")"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "703c4df0",
- "metadata": {},
- "outputs": [],
- "source": [
- "using SIMD"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "f18cdb48",
- "metadata": {},
- "outputs": [],
- "source": [
- "function simd_sum_vectors!(a::Array, b::Array)\n",
- " c = similar(a)\n",
- " @inbounds @simd for i in eachindex(a, b)\n",
- " c[i] = a[i] + b[i]\n",
- " end\n",
- "end"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "4e9e140f",
- "metadata": {},
- "outputs": [],
- "source": [
- "res2 = simd_sum_vectors!(a, b);"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "2685f7e6",
- "metadata": {},
- "outputs": [],
- "source": [
- "simd_t! = @belapsed simd_sum_vectors!(a, b)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "d093fd8f",
- "metadata": {},
- "outputs": [],
- "source": [
- "times = [serial_t, simd_t, simd_t!]\n",
- "speedup = maximum(times) ./ times"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "a7491ceb",
- "metadata": {},
- "source": [
- "A lot of operations in Julia already uses SIMD Broadcasting!"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "726556ea",
- "metadata": {},
- "outputs": [],
- "source": [
- "operation = a .*b\n",
- "broad_t = @belapsed operation"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "dbced515",
- "metadata": {},
- "outputs": [],
- "source": [
- "times = [serial_t, simd_t, simd_t!, broad_t]\n",
- "speedup = maximum(times) ./ times"
- ]
- },
- {
- "cell_type": "markdown",
- "id": "114ab3db",
- "metadata": {},
- "source": [
- "## Resume \n",
- "- SIMD is data level parallelism.\n",
- "- When using SIMD macro, Julia re-arranges floating point additions — even if it would change the answer.\n",
- "- Depending on your CPU, this may lead to 2x or 4x or even 8x parallelism.\n",
- "- The parallelism can (sometimes) happen automatically.\n",
- "- Not necessary, it is not always signficantly fast, although it is easy to use.\n",
- "- Best for small, tight, innermost loops."
- ]
- },
- {
- "cell_type": "markdown",
- "id": "4133fe69",
- "metadata": {},
- "source": [
- "# CHECKPOINT\n",
- "\n",
- "Using these libraries:\n",
- "\n",
- "```julia\n",
- "using BenchmarkTools, Test, SIMD, InteractiveUtils\n",
- "```\n",
- "\n",
- "### **Q1** \n",
- "Consider the following function that sums all the elements of a vector: \n",
- "\n",
- "```julia\n",
- "A = rand(__put a BIGNUMBER here__) \n",
- "\n",
- "function simplesum(A) \n",
- " result = zero(eltype(A)) \n",
- " for i in eachindex(A) \n",
- " result += A[i] \n",
- " end \n",
- " return result \n",
- "end \n",
- "``` \n",
- "\n",
- "- Try to optimize it for bounds checks\n",
- "- Benchmark against the in-built julia function `sum`\n",
- "- Implement SIMD parallelization and compute the obtained speedup\n",
- "\n",
- "### **Q2**\n",
- "\n",
- "The following function estimates pi with n samples. \n",
- "\n",
- "```julia\n",
- "function estimatepi(n)\n",
- " area_circle = 0\n",
- " for i = 1:n\n",
- " x, y = rand(), rand();\n",
- " r = x^2 + y^2\n",
- " if r < 1.0\n",
- " area_circle +=1\n",
- " end\n",
- " end\n",
- " return 4* area_circle/n\n",
- "end\n",
- "```\n",
- "- Optimize it for bounds checks\n",
- "- Use `time()` function in order to measure elapsed execution time for the function\n",
- "- Parallelize the code in order to exploit SIMD\n",
- "- Compute relative error with respect to true Julia value of `PI`\n",
- "\n",
- "### **Q3** \n",
- "Write the function that computes the multiplication of two square matrices $ C = A \\times B$ of order $n$, namely: \n",
- "$$\n",
- "c_{ij} = \\sum_{k=1}^n{a_{ik}b_{kj}}\n",
- "$$\n",
- "\n",
- "- Invert the order of involved for loops to exploit row-major and column major ordering and collect different execution times in a dictionary\n",
- "- Try to optimize the function ensuring that the result is correct (by using test and built-in Julia matrix multiplication)\n",
- "- Is it possible to use SIMD for this problem?"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "id": "70d01b33",
- "metadata": {},
- "outputs": [],
- "source": []
- }
- ],
- "metadata": {
- "kernelspec": {
- "display_name": "Python 3 (ipykernel)",
- "language": "python",
- "name": "python3"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.10.9"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 5
-}
--
GitLab